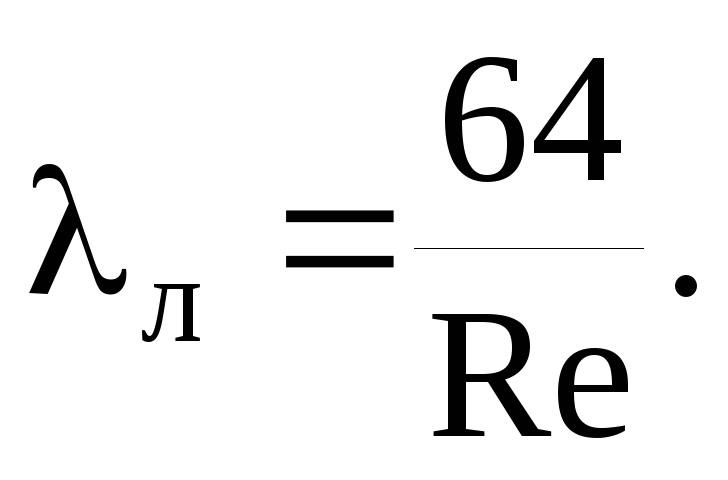1. Hidrosztatikus nyomás
A hidrosztatikus nyomás az
miatti belső nyomóerő
rájuk ható külső erők hatására
adott pont a folyadékban. Ilyen nyomás
minden irányban ugyanaz és attól függ
egy pont helyzetére egy folyadékban nyugalmi állapotban.
A hidrosztatikus nyomás mérete
az MKGSS rendszerben - kg / cm2 vagy t / m2,
SI rendszerben - N/m2.
Alapegységarányok
nyomás:
|
kg/cm2 |
N/m2 |
|
|
technikai légkör |
1 |
98066,5 |
|
milliméter vízoszlop |
0,0001 |
9,80665 |
|
higanymilliméter |
0,00136 |
133,32 |
Gyakorlati számításoknál 1 műszaki
atmoszféra \u003d 1 kg / cm2 \u003d 10 m víz. Művészet. =
735 Hgmm Művészet. = 98070 N/m2.
Egy összenyomhatatlan folyadékhoz, ami
egyensúlyban erő alatt
gravitációs, teljes hidrosztatikus
pontnyomás:
p=p+

ahol p a szabadra nehezedő nyomás
folyékony felület;

h magasság területtel
keresztmetszet egyenlő egy;
h - merülési mélység
pontok;

Egyes folyadékok esetében az értékek
megoldásánál használt fajsúly
A feladatokat a melléklet tartalmazza (tab.
P-3).
A túlnyomás értéke felett
légköri (oa)
manometrikusnak, ill
túlnyomás:

Ha a nyomás a szabad felületen
egyenlő légköri, majd többlet
nyomás pm=

Légkör alatti nyomás
a mennyiséget vákuumnak nevezzük:
Rwack= pa- R.
Ennek megoldása a legtöbb problémára
szakasz a használattal kapcsolatos
a hidrosztatika alapegyenlete

ahol z a koordináta vagy
pontjel.
1. Általános tudnivalók a csővezetékek hidraulikus számításairól
Számításkor
csővezetékeket fontolgatnak
állandó, egyenletes nyomás
bármilyen folyadék mozgása
turbulens rendszer, kerek-hengeres
csövek. Folyadék a nyomócsövekben
nyomás alatt van és
keresztmetszeteik teljesen
megtöltött. A folyadék mozgása mentén
csővezeték ennek eredményeként következik be
az a tény, hogy a nyomás az elején nagyobb, mint
a végén.
Hidraulikus
a számítást annak meghatározása érdekében végezzük
csővezeték átmérője d
egy ismert
hossza a kihagyás érdekében
egy bizonyos áramlási sebesség K
vagy létesítése
adott átmérőnél és a szükséges hossznál
nyomás és folyadékáramlás. Csővezetékek
azok hosszától és mintázatától függően
helyszínek vannak osztva egyszerű
és összetett. Egyszerű csővezetékekhez
magában foglalja azokat a csővezetékeket, amelyek nem rendelkeznek
hosszában elágazik, állandóval
ugyanaz a költség.
Csővezetékek
azonos átmérőjű csövekből állnak
teljes hosszában vagy különböző csőszakaszokból
átmérők és hosszúságok. Utolsó eset
soros kapcsolatra utal.
Egyszerű csővezetékek
hosszától függően egy telek helyi
ellenállásokat rövid és
hosszú. rövid
csővezetékek
vannak
kellően rövid hosszúságú csővezetékek,
amelyben helyi ellenállás
a hidraulika több mint 10%-át teszik ki
hosszvesztés. Például a következőket tartalmazzák:
szifon csövek, szívó
lapátos szivattyúk csövei, szifonok (nyomás
vízvezetékek az úttöltés alatt),
épületeken és építményeken belüli csővezetékek
stb.
hosszú
csővezetékek
hívott
a csővezetékek viszonylag nagyok
hosszúságok, amelyekben a fejveszteség a hossz mentén
számuk jelentősen meghaladja a helyieket
veszteség. A helyi veszteségek
kevesebb mint 5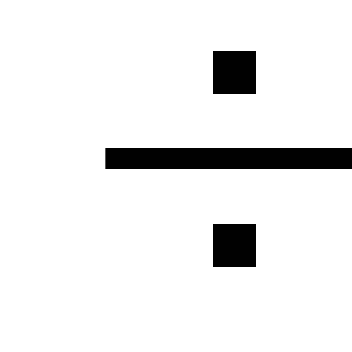
veszteségek a csővezeték hossza mentén, és ezért
elhanyagolhatók vagy bevezethetők at
hidraulikai számítások növekszik
együttható 1,05
Hosszú csővezetékek lépnek be a rendszerbe
vízellátó hálózatok, szivattyúvezetékek
állomások, vezetékek és csővezetékek
ipari vállalkozások és
mezőgazdasági célú és
stb.
Összetett csővezetékek
hosszában különböző ágaik vannak,
azok. csővezeték csőhálózatból áll
bizonyos átmérők és hosszúságok. Összetett
csővezetékek vannak osztva
párhuzamos, zsákutca (elágazó),
gyűrűs (zárt) csővezetékek,
szerepel a vízellátó hálózatban.
Hidraulikus
csővezeték számítása csökken, mint
általában három fő probléma megoldására:
-
meghatározás
csővezeték áramlás K,
ha ismert
nyomás H,
hossz l
és átmérője d
csővezeték,
tekintettel bizonyos helyi
ellenállások vagy ezek hiányában; -
meghatározás
szükséges nyomást H,
szükséges a bérlet biztosításához
ismert áramlás K
csővezetéken keresztül
hosszú l
és átmérője d; -
meghatározás
csővezeték átmérője d
mikor
ismert fejértékek H,
költség K
és hossza l.
A folyadék áramlási sebessége az
ahol q > tervezett folyadékáramlás, m3/s;
- a cső feszültség alatti szakaszának területe, m2.
A λ súrlódási ellenállási együtthatót az SP 40-102-2000 „Polimer anyagokból készült vízellátó és csatornarendszerek csővezetékeinek tervezése és szerelése” című szabályrendszer előírásai szerint határozzák meg. Általános követelmények":
ahol b a folyadékáramlási üzemmódok hasonlósági száma; b > 2 esetén b = 2-t veszünk.
ahol Re a tényleges Reynolds-szám.
ahol ν a folyadék kinematikai viszkozitásának együtthatója, m²/s. A hidegvíz-csövek kiszámításakor 1,31 10-6 m² / s - a víz viszkozitása +10 ° C hőmérsékleten;
Rekv > - Reynolds-szám, amely megfelel a hidraulikus ellenállás négyzetes tartományának kezdetének.
ahol Ke a csőanyag hidraulikus érdessége, m. Polimer anyagokból készült csövek esetén Ke = 0,00002 m-t kell venni, ha a csőgyártó nem ad meg más érdességértéket.
Azokban az áramlási esetekben, amikor Re ≥ Rekv, a b paraméter számított értéke 2 lesz, és a (4) képlet jelentősen leegyszerűsödik, átváltva a jól ismert Prandtl képletre:
Ke = 0,00002 m-nél a kvadratikus ellenállási tartomány 32,75 m/s vízhozamnál (ν = 1,31 10-6 m²/s) lép fel, ami a közüzemi vízellátó rendszerekben gyakorlatilag elérhetetlen.
A mindennapi számításokhoz a nomogramok ajánlottak, pontosabb számításokhoz pedig - "Táblázatok a polimer anyagokból készült csővezetékek hidraulikus számításaihoz", 1. kötet "Nyomású csővezetékek" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
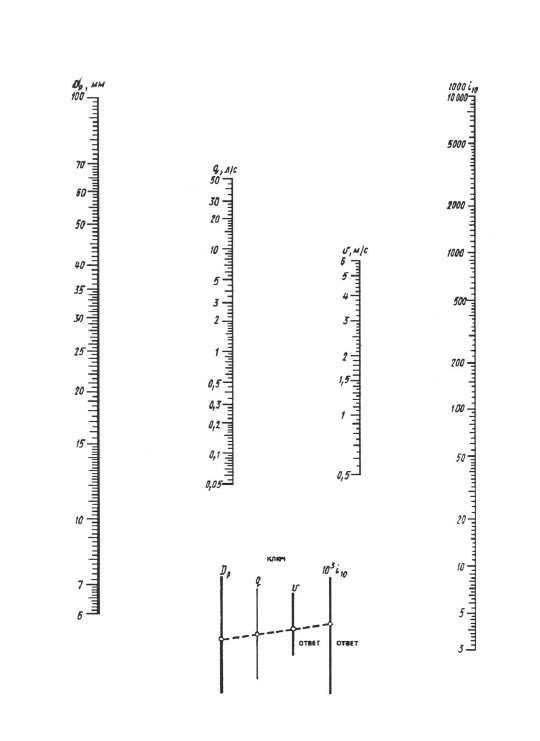
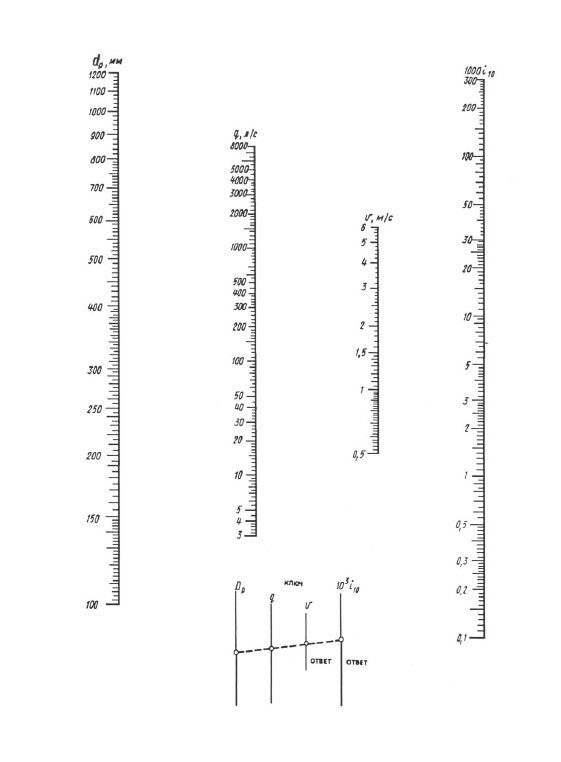
A nomogramok szerinti számítás során az eredményt a vonalzó egy átfedésével érjük el - a pontot a dp skálán a számított átmérő értékével kell összekötni a számított áramlási sebesség értékével a q-n (l / s) egyenes vonallal skálázzuk, ezt az egyenest addig folytassuk, amíg nem metszi a V sebesség és a fajlagos veszteségek 1000 i (mm/m) skáláját. Egy egyenes metszéspontjai ezekkel a skálákkal adják a V értéket és 1000 i-t.
Mint tudják, a folyadék szivattyúzásához szükséges villamos energia költsége egyenesen arányos H értékével (ceteris paribus). A (3) kifejezést a (2) képletbe behelyettesítve könnyen belátható, hogy az i (és ennek következtében a H) értéke fordítottan arányos a számított dp átmérővel ötödik fokig.
Fentebb látható, hogy a dp értéke a csőfal e vastagságától függ: minél vékonyabb a fal, annál nagyobb a dp, és ennek megfelelően annál kisebb a súrlódásból adódó nyomásveszteség és a villamos energia költsége.
Ha a cső MRS értéke bármilyen okból megváltozik, átmérőjét és falvastagságát (SDR) újra kell számolni.
Nem szabad megfeledkezni arról, hogy számos esetben az MRS 10-es csövek használata az MRS 8-as csövek helyett, különösen az MRS 6.3-as csövek használata lehetővé teszi a csővezeték átmérőjének egy mérettel történő csökkentését. Ezért korunkban a polietilén PE 80 (MRS 8) és PE 100 (MRS 10) használata a polietilén PE 63 (MRS 6.3) helyett a csövek gyártásához nemcsak a csövek falvastagságának, hanem tömegének csökkentését is lehetővé teszi. és anyagfelhasználás, hanem a folyadék szivattyúzásával kapcsolatos energiaköltségek csökkentése is (ceteris paribus).
Az elmúlt években (2013 után) a PE80 polietilénből készült csöveket a gyártásból szinte teljesen felváltották a PE100 minőségű polietilénből készült csövek. Ez azzal magyarázható, hogy az alapanyagokat, amelyekből a csövek készülnek, külföldről szállítják PE100 márkával.És az is, hogy a 100-as polietilénnek több szilárdsági jellemzője van, aminek köszönhetően a csövek ugyanolyan jellemzőkkel készülnek, mint a PE80-ból készült csövek, de vékonyabb falú, ezáltal növelve a polietilén csővezetékek áteresztőképességét.
Nomogram 6 100 mm átmérőjű csövek nyomásveszteségének meghatározására.
Nomogram 100, 1200 mm átmérőjű csövek nyomásveszteségének meghatározására.
Reynolds-kritérium
Ezt a függőséget Osborne Reynolds (1842-1912) angol fizikus és mérnök vetette fel.
Az a kritérium, amely segít megválaszolni azt a kérdést, hogy szükséges-e figyelembe venni a viszkozitást, a Reynolds-szám Re. Ez egyenlő az áramló folyadék elemének mozgási energiájának és a belső súrlódási erők munkájának arányával.
Tekintsünk egy n élhosszúságú köbös folyadékelemet. Egy elem kinetikus energiája:
Newton törvénye szerint a folyadékelemre ható súrlódási erőt a következőképpen határozzuk meg:
Ennek az erőnek a munkája egy folyékony elem n távolságra történő mozgatásakor
a folyadékelem mozgási energiájának és a súrlódási erő munkájának aránya pedig az
Csökkentjük és megkapjuk:
Re-t Reynolds-számnak hívják.
Így Re egy dimenzió nélküli mennyiség, amely a viszkózus erők relatív szerepét jellemzi.
Például, ha annak a testnek a méretei, amellyel a folyadék vagy gáz érintkezik, nagyon kicsik, akkor még alacsony viszkozitás mellett is jelentéktelen lesz az Re, és a súrlódási erők játszanak túlnyomó részt. Ellenkezőleg, ha a test méretei és a sebessége nagyok, akkor Re >> 1 és még a nagy viszkozitás sem lesz szinte semmilyen hatással a mozgás természetére.
A nagy Reynolds-számok azonban nem mindig azt jelentik, hogy a viszkozitás nem játszik szerepet. Tehát amikor az Re-szám nagyon nagy (több tíz- vagy százezres) értékét elérjük, a sima lamináris (a latin lamina - „lemez”) áramlás turbulenssé válik (a latin turbulentus - „viharos” szóból). , „kaotikus”), kaotikus, bizonytalan mozgások kíséretében folyadékok. Ez a hatás akkor figyelhető meg, ha fokozatosan nyitunk egy vízcsapot: egy vékony patak általában egyenletesen folyik, de a víz sebességének növekedésével az áramlás simasága megzavarodik. A nagy nyomás alatt kiáramló sugárban a folyékony részecskék véletlenszerűen, oszcillálva mozognak, minden mozgást erős keveredés kísér.
A turbulencia megjelenése nagymértékben növeli a légellenállást. Csővezetékben a turbulens áramlási sebesség kisebb, mint a lamináris áramlási sebesség azonos nyomásesések mellett. De a turbulencia nem mindig rossz. Tekintettel arra, hogy a turbulencia közbeni keveredés igen jelentős, a hőátadás - az aggregátumok hűtése vagy melegítése - sokkal intenzívebben megy végbe; a kémiai reakciók gyorsabban terjednek.
Bernoulli stacionárius mozgásegyenlete
A hidromechanika egyik legfontosabb egyenletét Daniel Bernoulli (1700-1782) svájci tudós állította fel 1738-ban. Először sikerült leírnia egy ideális folyadék mozgását a Bernoulli-képletben kifejezve.
Az ideális folyadék olyan folyadék, amelyben az ideális folyadék elemei, valamint az ideális folyadék és az edény falai között nincsenek súrlódási erők.
Az ő nevét viselő álló mozgás egyenlete:
ahol P a folyadék nyomása, ρ a sűrűsége, v a mozgás sebessége, g a szabadesés gyorsulása, h az a magasság, amelyen a folyadék eleme található.
A Bernoulli-egyenlet jelentése, hogy egy folyadékkal töltött rendszeren belül (csővezetékszakasz) az egyes pontok összenergiája mindig változatlan.
A Bernoulli-egyenlet három tagból áll:
- ρ⋅v2/2 - dinamikus nyomás - a hajtófolyadék térfogategységére eső mozgási energia;
- ρ⋅g⋅h - súlynyomás - egységnyi térfogatú folyadék potenciális energiája;
- P - statikus nyomás, eredete nyomóerők munkája, és nem jelent semmilyen speciális energiafajta tartalékát („nyomásenergia”).
Ez az egyenlet megmagyarázza, hogy a cső szűk szakaszain miért nő az áramlási sebesség, és miért csökken a csőfalakra ható nyomás. A maximális nyomás a csövekben pontosan azon a helyen van beállítva, ahol a cső legnagyobb keresztmetszete van. A cső keskeny részei ebből a szempontból biztonságosak, de bennük a nyomás annyira leeshet, hogy a folyadék felforr, ami kavitációhoz és a csőanyag tönkremeneteléhez vezethet.
Navier-Stokes egyenlet viszkózus folyadékokra
Egy szigorúbb megfogalmazásban a viszkózus súrlódás lineáris függését a folyadéksebesség változásától Navier-Stokes egyenletnek nevezik. Figyelembe veszi a folyadékok és gázok összenyomhatóságát, és Newton törvényétől eltérően nem csak a szilárd test felülete közelében érvényes, hanem a folyadék minden pontján (összenyomhatatlan test esetén a szilárd test felületének közelében is) folyadék, a Navier-Stokes egyenlet és a Newton-törvény egybeesik).
Minden olyan gáz, amelyre a folytonos közeg feltétele teljesül, a Navier-Stokes egyenletnek is megfelel, azaz. newtoni folyadékok.
A folyadékok és gázok viszkozitása általában viszonylag kis sebességeknél jelentős, ezért néha azt mondják, hogy az Euler-hidrodinamika a Navier-Stokes hidrodinamika nagy sebességeinek speciális (korlátozó) esete.
Alacsony sebességnél a viszkózus súrlódás Newton-törvényének megfelelően a test húzóereje arányos a sebességgel. Nagy sebességeknél, amikor a viszkozitás már nem játszik jelentős szerepet, a test ellenállása arányos a sebesség négyzetével (amit először Newton fedezett fel és támasztott alá).
Hidraulikus számítási sorrend
1.
A fő keringés van kiválasztva
gyűrűs fűtési rendszer (a legtöbb
hátrányosan a hidraulikában helyezkedik el
kapcsolat). Zsákutcában kétcsöves
rendszerek egy áthaladó gyűrű
alsó hangszer a legtávolabbi és
terhelt felszálló, egycsöves -
keresztül a legtávolabbi és betöltött
felszálló.
Például,
kétcsöves fűtési rendszerben
felső vezetékek fő keringése
a gyűrű átmegy a hőponttól
a fő felszállón, tápvezetéken keresztül,
a legtávolabbi felszállón keresztül, fűtés
földszinti készülék, visszatérő vezeték
a fűtési ponthoz.
V
rendszerekhez kapcsolódó vízmozgással
a gyűrűt veszik főnek,
leginkább a közepén halad át
terhelt állvány.
2.
A fő keringtető gyűrű eltörik
parcellákba (a cselekmény jellemző
állandó vízáramlás és ugyanaz
átmérő). A diagram azt mutatja
szakaszszámok, hosszuk és termikus
terhelések. A fő hőterhelése
telkeket összegzéssel határozzuk meg
ezek által kiszolgált hőterhelések
telkek. A csőátmérő kiválasztásához
két mennyiséget használnak fel:
a)
adott vízáramlás;
b)
közelítő fajlagos nyomásveszteségek
súrlódásra a tervezési körforgásban
gyűrű RHázasodik.
Mert
számítás Rcp
tudnia kell a fő hosszát
cirkulációs gyűrűt és kiszámították
keringési nyomás.
3.
A számított keringés
képlet nyomás
 ,
,
(5.1)
ahol
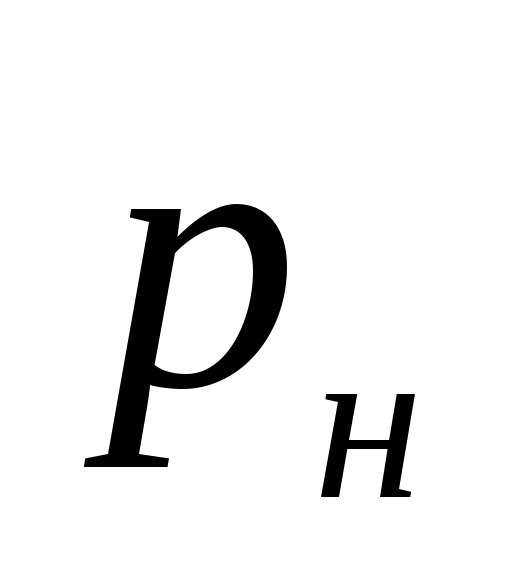
a szivattyú által létrehozott nyomás, Pa.
Rendszertervezési gyakorlat
fűtés mutatta, hogy a legtöbb
célszerű a szivattyú nyomását venni,
egyenlő
 ,
,
(5.2)
ahol
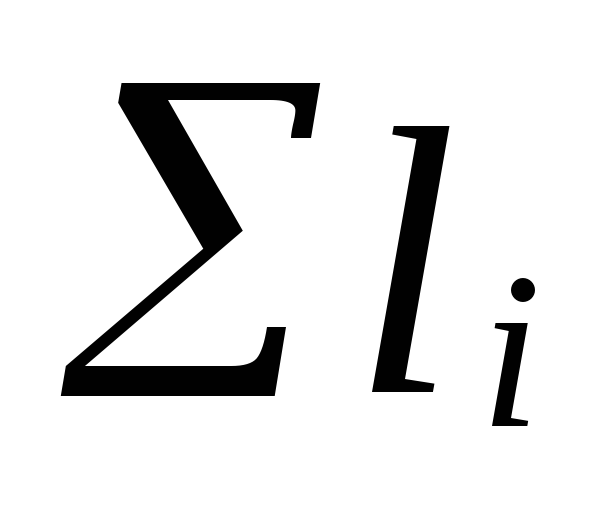
a főforgalom szakaszai hosszának összege
gyűrűk;
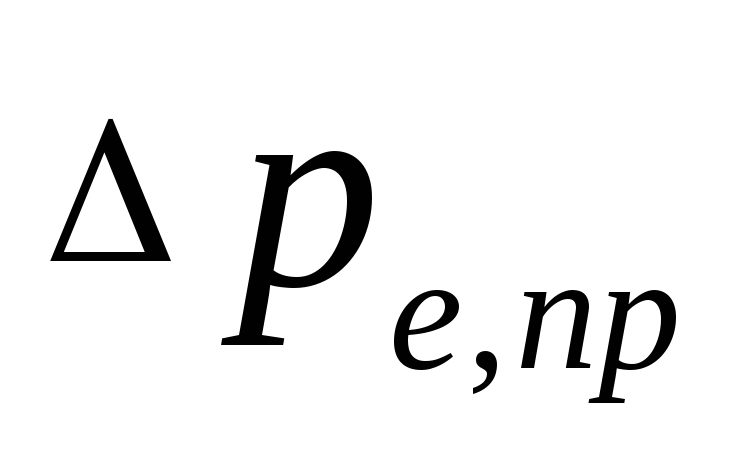
természetes nyomás, amely akkor jelentkezik, amikor
vízhűtés készülékekben, Pa, lehetséges
határozza meg, hogyan
 ,
,
(5.3)
ahol
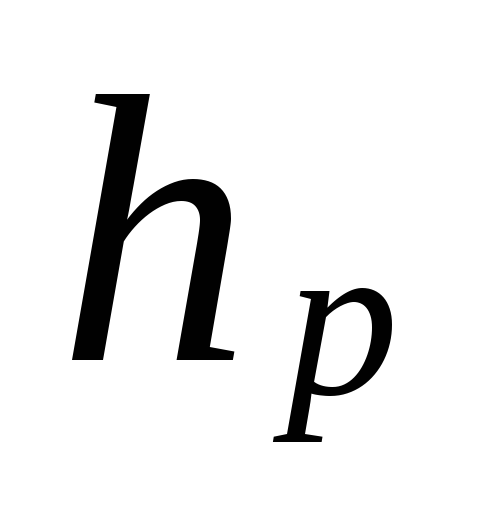
távolság a szivattyú (lift) közepétől
az alsó szint készülékének közepéig, m.
Jelentése
együttható lehetséges
meghatározza az 5.1. táblázatból.
asztal
5.1 – Jelentés c
a tervezési hőmérséklettől függően
víz a fűtési rendszerben
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
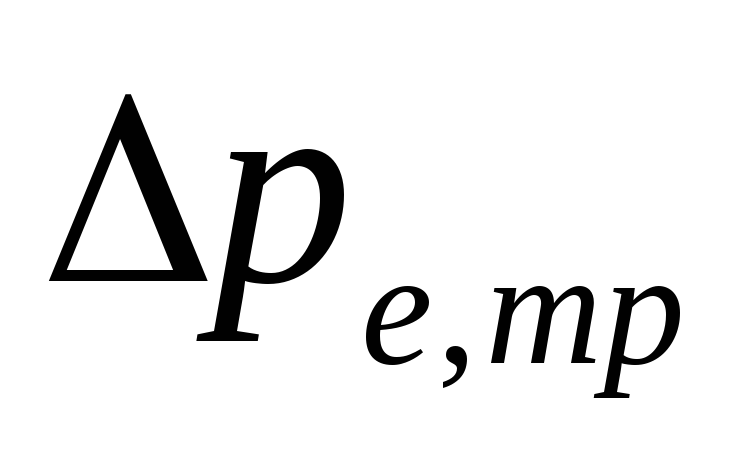
természetes nyomás be
a csővezetékek vízhűtése következtében
.
V
szivattyúrendszerek alsó vezetékekkel
nagyságrendű
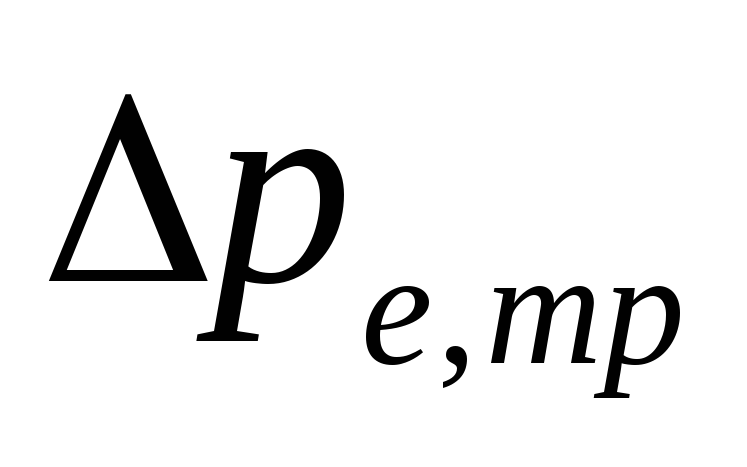
-
Határozottak
fajlagos súrlódási nyomásveszteség
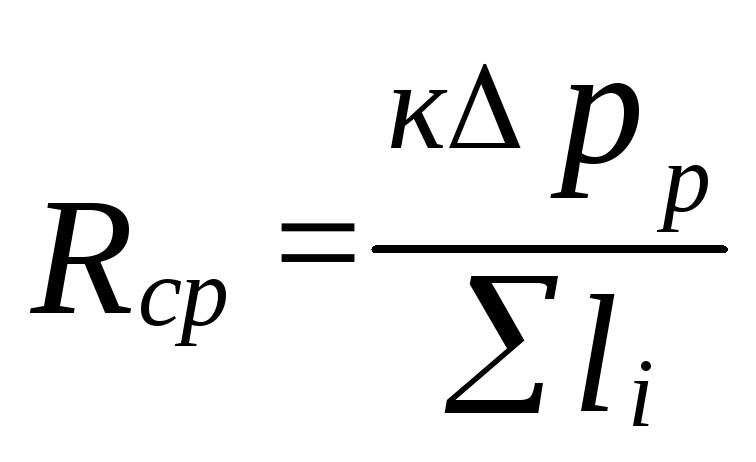
(5.4)
ahol
k=0,65 határozza meg a nyomásveszteségek arányát
súrlódáshoz.
5.
A területen a vízhozamot a
képlet
 (5.5)
(5.5)
ahol
K
- hőterhelés a telephelyen, W:
(tG
— tO)
- a hűtőfolyadék hőmérséklet-különbsége.
6.
Nagyságrend szerint
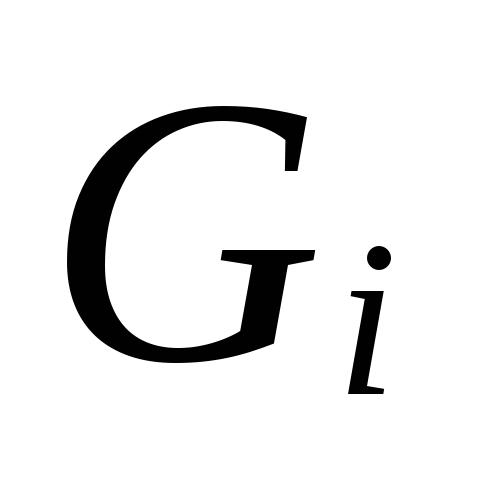
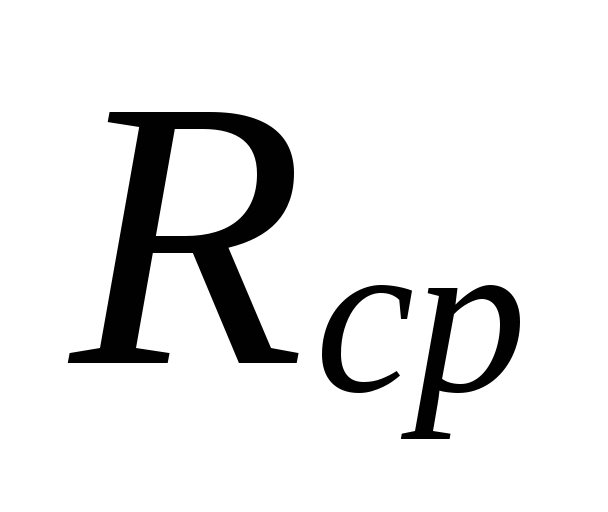
.

6.
A kiválasztott csővezeték átmérőkhöz
és meghatározzák a becsült vízfogyasztást
hűtőfolyadék sebessége v
és a tényleges konkrét
súrlódási nyomásveszteség Rf.
Nál nél
átmérők kiválasztása kis területeken
hűtőfolyadék áramlási sebessége lehet
között nagy eltérések vannak
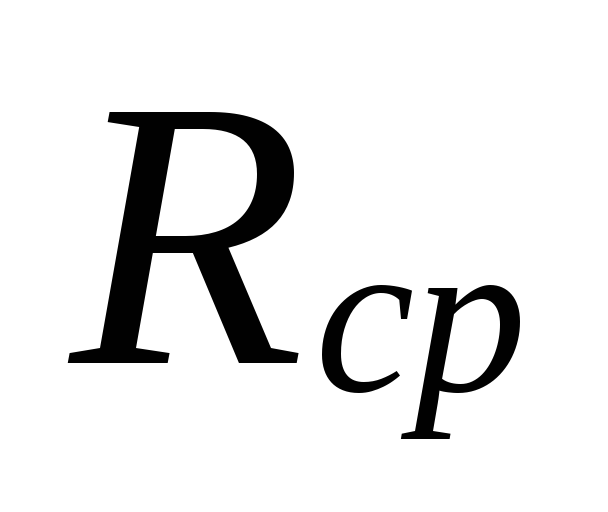
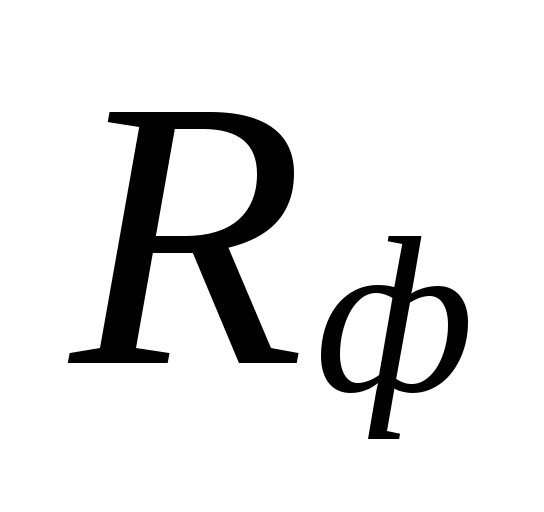
alábecsült veszteségek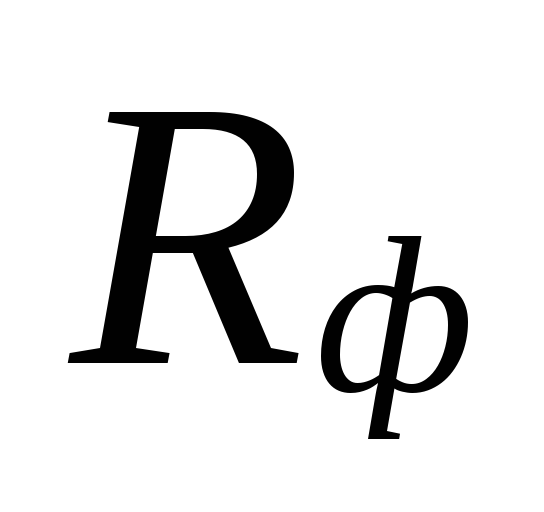
ezeket a területeket túlbecsléssel kompenzálják
mennyiségeket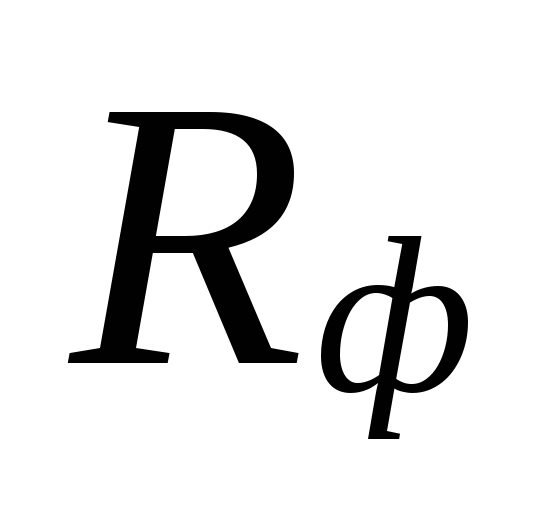
7.
Meghatározzák a súrlódási nyomásveszteségeket
a számított területen, Pa:
 .
.
(5.6)
eredmények
a számításokat az 5.2. táblázat tartalmazza.
8.
Nyomásveszteség helyi
ellenállások a következő képlet segítségével:
 ,
,
(5.7)
ahol
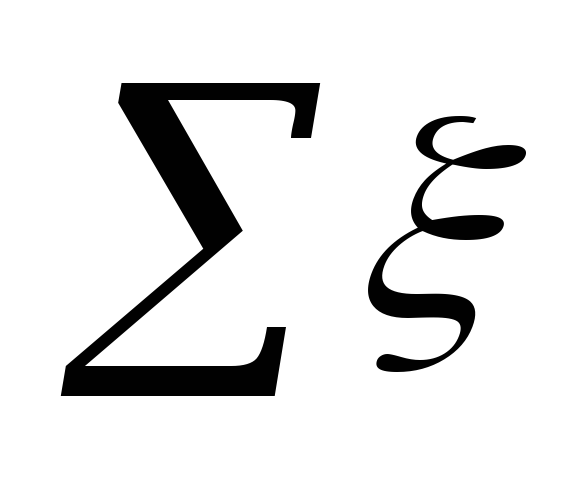
a település területén.
Jelentése ξ
táblázatban foglaltuk össze. 5.3.
5.3. táblázat -
Helyi ellenállási együtthatók
|
sz. p / p |
Nevek |
Értékek |
Megjegyzések |
9.
Határozza meg a teljes nyomásveszteséget
minden területen
 .
.
(5.8)
10. Határozza meg
a súrlódás miatti teljes nyomásveszteség és
a helyi ellenállásokban fő
keringő gyűrű
 .
.
(5.9)
11. Hasonlítsa össze Δp
Val vel ΔpR.
Teljes nyomásveszteség a gyűrűben
kisebbnek kell lennie, mint ΔpR
a
 .
.
(5.10)
eldobható készlet
nyomásra van szükség az el nem számolt in
hidraulikus ellenállás számítása.
Ha a feltételek nem
végrehajtják, bizonyos esetekben szükséges
a gyűrű szakaszait a csövek átmérőjének megváltoztatásához.
12. Számítás után
fő keringési gyűrű
készítse el a fennmaradó gyűrűk összekapcsolását. V
csak minden új gyűrű számít
további nem közös területek,
szakaszokkal párhuzamosan csatlakozik
főgyűrű.
Veszteség eltérés
nyomás párhuzamosan kapcsolva
parcellák 15%-ig megengedettek zsákutcával
a víz mozgása és akár 5% - áthaladással.
asztal
5.2 - A hidraulikus számítások eredményei
fűtési rendszerhez
|
A |
Által |
Által |
||||||||||||||
|
Szám |
termikus |
Fogyasztás |
Hossz |
Átmérő |
Sebesség |
Különleges |
Veszteség |
Összeg |
Veszteség |
d, |
v, |
R, |
Δptr, |
∑ξ |
Z, |
Rl+Z, |
6. lecke
A gáz hőmérsékletének változása a gázvezeték hosszában
Álló gázáramlásban a tömeg
az áramlási sebesség a gázvezetékben az
 . (2.41)
. (2.41)
Valójában a gáz mozgása a gázvezetékben
mindig nem izoterm. V
A tömörítés során a gáz felmelegszik.
Még a COP-on történő lehűlés után is a hőmérséklet
gáz belép a vezetékbe
körülbelül 2040С,
ami sokkal magasabb a hőmérsékletnél
környezet (T).
A gyakorlatban a gáz hőmérséklete válik
közel a környezeti hőmérséklethez
csak kis átmérőjű gázvezetékekhez
(Dy0.
Sőt, azt is figyelembe kell venni
vezetékes gáz
valódi gáz, ami velejárója
a Joule-Thompson effektus, amely figyelembe veszi
hőfelvétel a gáz expanziója során.
Amikor a hőmérséklet a hossz mentén változik
gázvezeték gázmozgás leírása
egyenletrendszer:
fajlagos energia ,
,
folytonosság ,
,
Államok ,
,
hőegyensúly .
.
Tekintsük az első közelítésben az egyenletet
hőegyensúly a hatás figyelembevétele nélkül
Joule Thompson. Az egyenlet integrálása
hőegyensúly
 ,
,
kapunk
 , (2.42)
, (2.42)
ahol ;
;
KSR- átlagosan az oldalon teljes
hőátbocsátási tényező a gázról a
környezet;
G a gáz tömegáramlási sebessége;
cP–
a gáz átlagos izobár hőkapacitása.
egy értéktL-t dimenzió nélküli kritériumnak nevezzük
Shukhov
 (2.43)
(2.43)
Tehát a gáz hőmérséklete a végén
gázvezeték lesz
 . (2.44)
. (2.44)
Az elejétől x távolságban
gázvezeték gázhőmérséklet határozza meg
képlet szerint
 . (2.45)
. (2.45)
A hőmérséklet változása a gázvezeték hosszában
exponenciális (ábra).
2.6).
Fontolgat
a gázhőmérséklet változásának hatása
csővezeték teljesítménye.
A fajlagos egyenlet mindkét oldalának szorzata
energia a 2-n és kifejezve ,
,
kapunk
 . (2.46)
. (2.46)
A gáz sűrűségét a bal oldalon fejezzük ki
kifejezések (2.46) az állapotegyenletből
 ,
,
szorzatw a folytonossági egyenletből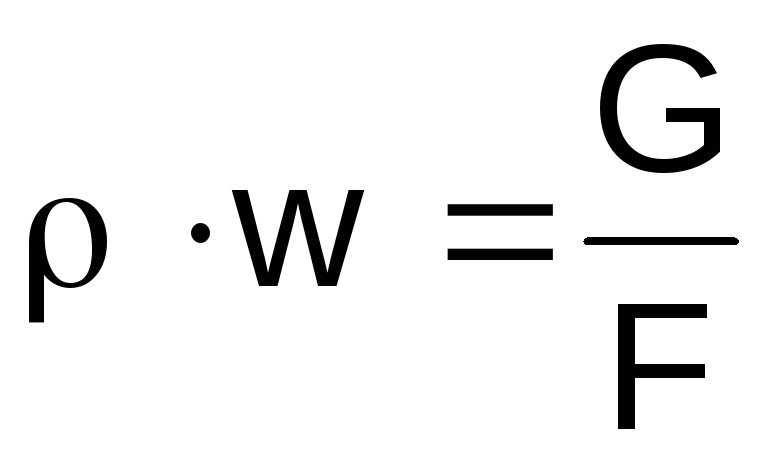
egyensúly .
.
Ezt szem előtt tartva a fajlagos egyenlet
az energia formát ölt
 (2.47)
(2.47)
vagy
 . (2.48)
. (2.48)
Jelölve
 és integráljuk az egyenlet bal oldalát
és integráljuk az egyenlet bal oldalát
(2,48) P-tőlHdoPNAK NEK, és a T-től jobbraHpontNAK NEK, kapunk
 . (2.49)
. (2.49)
Cserélésével
 , (2.50)
, (2.50)
nekünk van
 . (2.51)
. (2.51)
Integrálás után a megadott
korlátokat kapunk

 . (2.52)
. (2.52)
Figyelembe véve (2.42)

vagy
 , (2.53)
, (2.53)
ahol egy korrekciós tényező, amely figyelembe veszi
egy korrekciós tényező, amely figyelembe veszi
hőmérsékletváltozás a gázvezeték hossza mentén
(a gázáramlás nem izotermitása).
Figyelembe véve (2.53), a függést a meghatározásához
A gáz tömegáramlási sebessége a formát veszi fel
 . (2.54)
. (2.54)
Érték Hmindig nagyobb, mint egy, tehát
a gáz tömegáramlási sebessége változáskor
hőmérséklet a gázvezeték hosszában
(nem izoterm áramlási mód) mindig
kevesebb, mint izoterm üzemmódban
(T=idem). Termék THátlagos integrálnak nevezzük
a csővezetékben lévő gáz hőmérséklete.
A Shukhov szám értékeivel Shu4
gázáramlás a csővezetékben
szinte izotermnek tekintjük
at T=idem. Ilyen hőmérséklet
üzemmód lehetséges, ha gázt pumpál vele
alacsony gázvezeték költség
kicsi (500 mm-nél kisebb) átmérőjű vagy jelentős
távolság.
A gázhőmérséklet változásának hatása
megnyilvánul a Shukhov-szám értékeinél
Shu
Nál nél
gázszivattyúzás fojtószelep jelenléte
hatása mélyebbre vezet
gázhűtés, mint csak hőcserével
talajjal. Ebben az esetben a hőmérséklet
a gáz akár alá is csökkenhet
hőmérséklet T (ábra.
2.7).
Rizs. 2.7. A Joule-Thompson effektus hatása
a gáz hőmérséklet-eloszlásáról
csővezeték hossza
1 - Di figyelembevétele nélkül; 2 - -val
figyelembe véve Di
Ezután figyelembe véve a Joule-Thompson együtthatót
a hőmérséklet változás törvénye a hossz mentén
felveszi a formát
 , (2.55)
, (2.55)
5 Hidraulikus veszteségek
Különbség
olajnyomás az egyik két szakaszában
és ugyanaz a csővezeték, feltéve, hogy
az első a folyásiránnyal szemben helyezkedik el, és
a második - lent - van meghatározva egyenlet
Bernoulli
 ,
,
ahol
h2
– h1
- a súlypontok magasságkülönbsége
szakaszokat egy tetszőlegesen választottból
vízszintes szint;
v1,
v2
– az olaj átlagos sebessége szakaszokban;
g - erőgyorsulás
gravitáció;

hidraulikus veszteségek mozgás közben
olajok az első szakasztól a másodikig.
Az egyenlet
Bernoulli teljes használatban
szivattyúk szívóvezetékeinek kiszámításához;
más esetekben az első tag,
általában figyelmen kívül hagyják és figyelembe veszik:

hidraulikus
a veszteségeket általában helyi
veszteségek és súrlódási veszteségek a hossz mentén
csővezetékek (lineáris).
1.5.1
helyi veszteségek
az energiák a helyinek köszönhetők
hidraulikus ellenállás,
áramlási torzulást okozva. Helyi
az ellenállások a következők: szűkületek,
csővezetékek bővítése, lekerekítése,
szűrők, vezérlő berendezések és
szabályozás stb.. Áramláskor
folyadékok helyi ellenállásokon keresztül
sebessége változik és általában vannak
nagy örvények.
Veszteség
a helyi ellenállások nyomása
képlet határozza meg Weisbach:
 MPa
MPa
(vagy
 pa),
pa),
ahol

veszteség,
v
az átlagos áramlási sebesség a keresztmetszetben
helyi ellenállás mögötti csőben, m/s;
,
N/m3;
g = 9,81 m/s2.
Minden egyes
helyi ellenállás jellemzi
együttható értékével

Turbulens áramlással az értékek
ellenállás és nagyon kevés változás
a szakasz méretének, sebességének változásával
folyadékáramlás és viszkozitás. Így
tételezzük fel, hogy nem a számtól függenek
Reynolds Re.
Értékek

például a pólókhoz ugyanazzal
a csatornaátmérőket egyenlőnek veszik,
ha:
patakok
összead, eltér; folyam
elhaladó;









nál nél
csőhajlat

Értékek

berendezések hidraulikus rendszereiben, in
referencia irodalom.
Nál nél
lamináris áramlás (Re
Veszteség
a helyi ellenállások nyomása at
a lamináris áramlást határozzák meg
képlet:
 MPa
MPa
ahol

= a

Mennyiségek
nyomásveszteség szabványban
hidraulikus berendezések
névleges áramlási sebesség általában
műszaki leírásukban szerepelnek.
1.5.2
Veszteség tovább
hosszanti súrlódás
a fellépő energiaveszteség
állandó keresztmetszetű egyenes csövekben,
azok. egyenletes folyadékáramlással,
és a hosszával arányosan növeljük
csövek. Ezek a veszteségek belső eredetűek
súrlódás a folyadékban, ezért van
durva és sima csövekbe egyaránt helyezzük.
Veszteség
csővezeték súrlódási nyomása
képlet határozza meg Darcy:
 MPa
MPa
ahol

l
és d
- a csővezeték hossza és belső átmérője,
mm.
Ez
a képlet laminárisra is alkalmazható,
valamint turbulens áramlásban; különbség
csak az együttható értékeiből áll

Nál nél
lamináris áramlás (Re
Nál nél
turbulens áramlási súrlódási tényező
nem csak a Re függvénye, hanem
a belső érdességétől is függ
cső felülete. Mert hidraulikusan
sima csövek,
azok. olyan érdességgel, hogy
gyakorlatilag nem befolyásolja az ellenállását,
turbulens súrlódási együttható
mód a képlettel határozható meg PC.
Konakova:

cső
hidraulikusan simának számít, ha
(d/k)>(Re/20),
ahol k az egyenértékű érdesség,
mm. Például új varrat nélküli acélhoz
csövek k≈0,03
mm, és több éves működés után
k≈0,2
mm-ből készült új varrat nélküli csövekhez
színesfémek k≈0,005
mm. Ezeket a csöveket gyakran használják
szerszámgépek hidraulikus rendszerei.
Együttható
súrlódás a turbulens rendszerben lehet
képlettel határozzuk meg Altshulya,
univerzális (azaz alkalmazható
mindenesetre):

2. A csővezeték áramlási moduljának áramlási jellemzői
Emlékezzünk
lineáris veszteség képlet - Darcy formula
- Weisbach:
 .
.
Expressz
ebben a képletben az V sebesség
Q áramláson keresztül
az aránytól
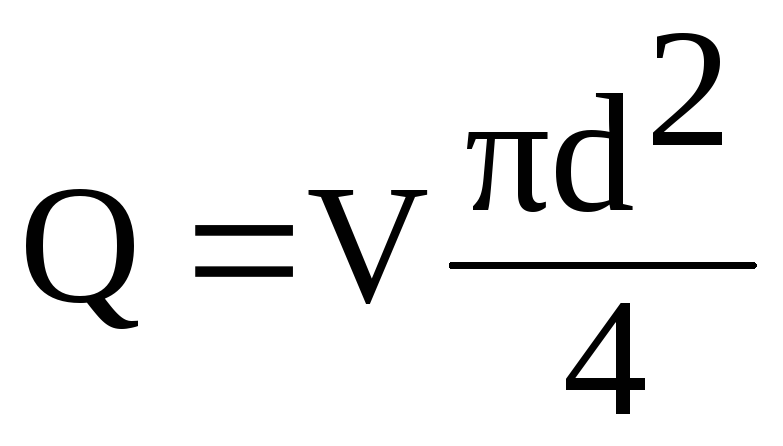
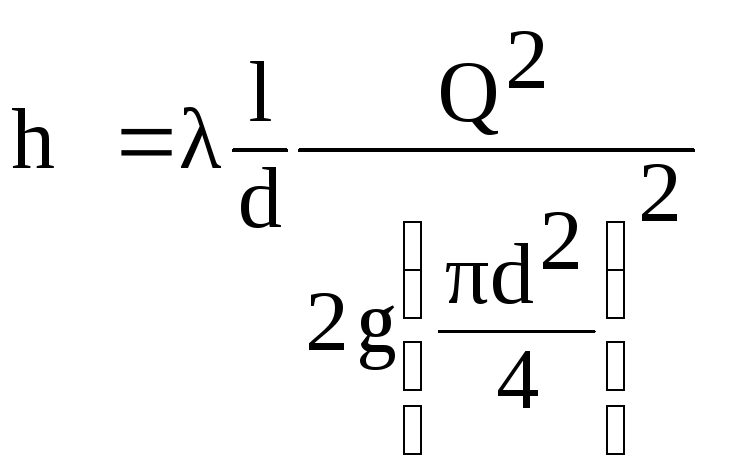
(6.1)
Mert
egy bizonyos átmérőjű csővezeték
mennyiségek komplexuma
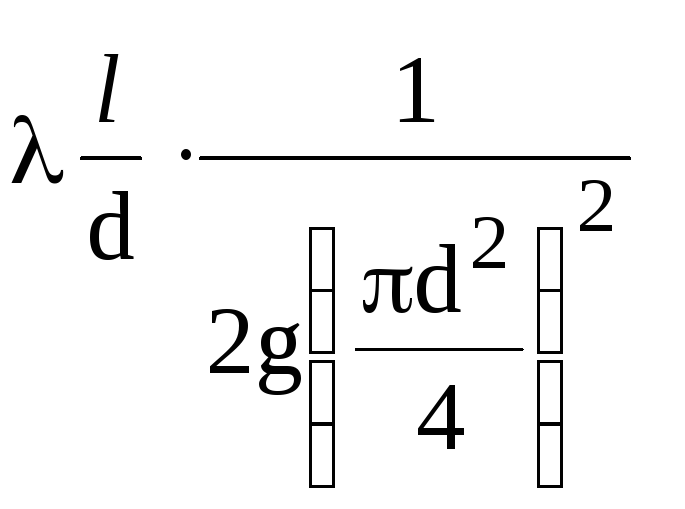
állandó (1/K2),
kivéve a hidraulikus együtthatót
súrlódás λ. A koncepció alapján
átlagos gazdasági sebesség Vs.e
mutassuk meg, hogy a jelzett együttható λ
ennek a komplexusnak tulajdonítható, mert v
Ebben az esetben a Reynolds-szám lesz
konkrét jelentése van:
 ,
,
a Nikuradze parcellán pedig a λ in együttható
ennek az esetnek konkrét lesz
jelentése.
Indokolja meg
a fogalom bevezetésének legitimitása
átlagos gazdasági sebessége az alábbiak szerint
érvelés.
hidraulikus
rendszer, például vízvezeték,
kihagyhat egy bizonyos kiadást
különböző átmérőjű csövekből készült. Nál nél
Ugyanakkor a d átmérő növekedésével,
ezért az V sebesség csökkenése
a tőkekiadások emelkedni fognak, és
működési költségei lesznek
csökkenés a hidraulika csökkenése miatt
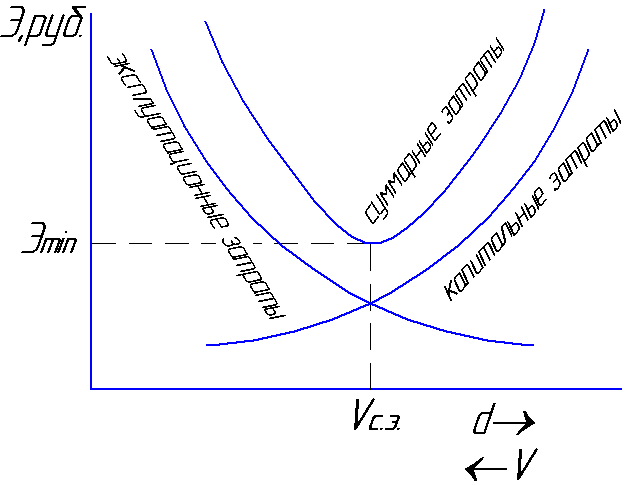
veszteség. Az a sebesség, amellyel a teljes
költségek minimálisak lesznek
átlagos gazdaságinak fogják nevezni
V sebességs.e
= 0,8 ... 1,3 m / s (6.1. ábra).
ábra.6.1
Azután
a lineáris veszteségképlet (6.1) alakot ölt
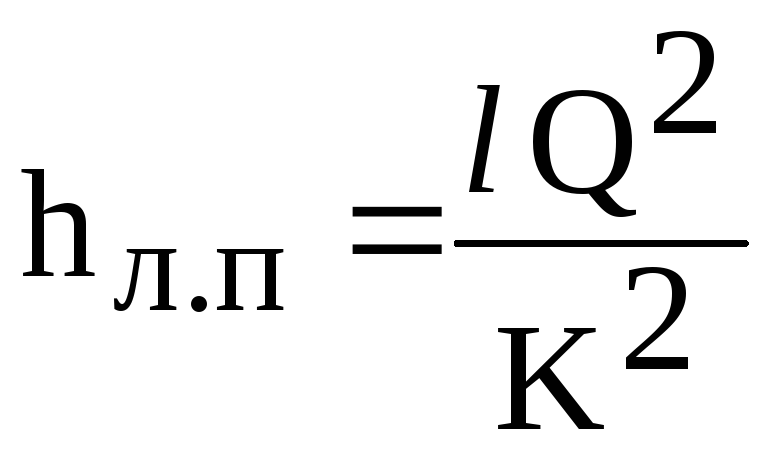
(6.2)
ahol
K - a csővezetékre jellemző áramlás
(áramlási modulus), anyagtól függően
csővezeték, átmérő és áramlás. Elrabolva
táblázatokból.
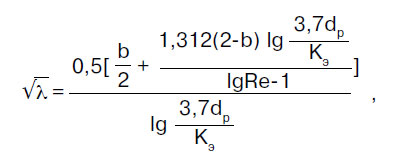
 ),C
),C ,
,