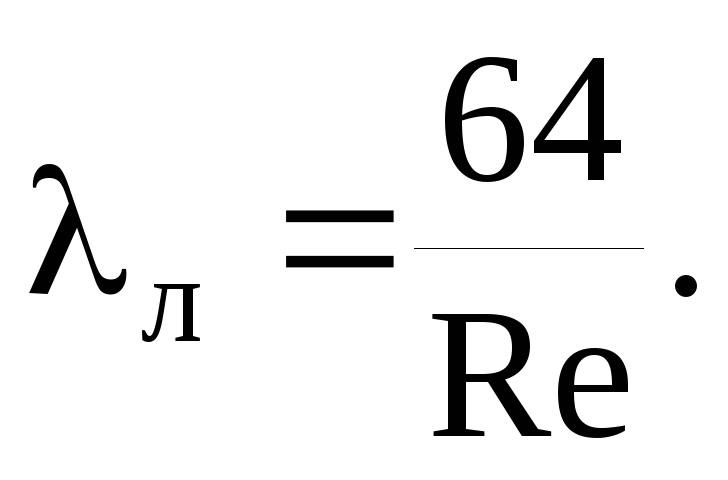1. Pressão hidrostática
A pressão hidrostática é
força de compressão interna devido a
pela ação de forças externas aplicadas
dado ponto no fluido. Tal pressão
em todas as direções é o mesmo e depende
sobre a posição de um ponto em um fluido em repouso.
Dimensão da pressão hidrostática
no sistema MKGSS - kg/cm2 ou t/m2,
no sistema SI - N/m2.
Proporções de unidades básicas
pressão:
|
kg/cm2 |
N/m2 |
|
|
atmosfera técnica |
1 |
98066,5 |
|
milímetro de coluna de água |
0,0001 |
9,80665 |
|
milímetro de mercúrio |
0,00136 |
133,32 |
Em cálculos práticos, 1 técnico
atmosfera \u003d 1 kg / cm2 \u003d 10 m de água. Arte. =
735 mmHg Arte. = 98070 N/m2.
Para um fluido incompressível que é
em equilíbrio sob força
gravidade, totalmente hidrostático
pressão do ponto:
p=p+

onde p é a pressão sobre o livre
superfície líquida;

altura h com área
seção transversal igual a um;
h - profundidade de imersão
pontos;

Para alguns líquidos, os valores
gravidade específica usada para resolver
tarefas são dadas no apêndice (tab.
P-3).
O valor do excesso de pressão sobre
atmosférico (pág.uma)
chamado manométrico, ou
sobrepressão:

Se a pressão na superfície livre
igual ao atmosférico, então o excesso
pressão pm=

Sob pressão atmosférica
a quantidade é chamada de vácuo:
Rmaluco= puma- R
A solução para a maioria dos problemas deste
seção está relacionada ao uso
a equação básica da hidrostática

onde z é a coordenada ou
marca de ponto.
1. Informações gerais sobre o cálculo hidráulico de tubulações
Ao calcular
dutos sendo considerados
pressão constante e uniforme
movimento de qualquer fluido
regime turbulento, em cilindros redondos
tubos. Fluido em tubos de pressão
está sob pressão e
suas seções transversais são completamente
preenchidas. O movimento do fluido ao longo
pipeline ocorre como resultado
o fato de que a pressão no início dela é maior do que
no fim.
Hidráulico
o cálculo é feito para determinar
diâmetro da tubulação d
com um conhecido
comprimento para garantir salto
uma certa vazão Q
ou estabelecendo
em um determinado diâmetro e comprimento do necessário
pressão e fluxo de fluido. Oleodutos
dependendo do comprimento e padrão de sua
locais são divididos em simples
e complexo. Para pipelines simples
inclui tubulações que não têm
ramos ao longo do comprimento, com uma constante
a mesma despesa.
Oleodutos
consistem em tubos do mesmo diâmetro
ao longo de todo o comprimento ou de seções de tubos de diferentes
diâmetros e comprimentos. Último caso
refere-se a uma conexão serial.
Pipelines simples
dependendo do comprimento com um gráfico de local
resistências são divididas em curtas e
grandes. baixo
oleodutos
são
oleodutos com um comprimento suficientemente curto,
em que a resistência local
compõem mais de 10% da hidráulica
perda de comprimento. Por exemplo, eles incluem:
tubos de sifão, sucção
tubos de bombas de palhetas, sifões (pressão
tubos de água sob o aterro da estrada),
tubulações dentro de edifícios e estruturas
etc.
grandes
oleodutos
chamado
as tubulações são relativamente grandes
comprimentos em que a perda de carga ao longo do comprimento
superam significativamente os locais
perdas. As perdas locais são
menos de 5
perdas ao longo do oleoduto e, portanto,
podem ser negligenciados ou introduzidos
cálculos hidráulicos aumentando
coeficiente igual a 1,05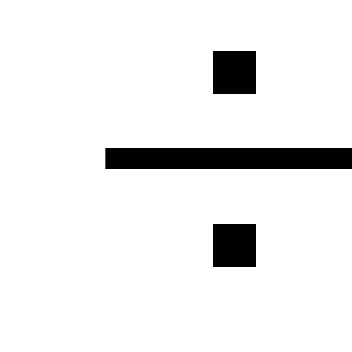
Longos dutos entram no sistema
redes de abastecimento de água, condutas de bombagem
estações, condutas e condutas
empresas industriais e
finalidade agrícola e
etc.
Pipelines complexos
têm ramos diferentes ao longo do comprimento,
Essa. pipeline consiste em uma rede de tubos
certos diâmetros e comprimentos. Complexo
dutos são divididos em
paralelo, beco sem saída (ramificado),
dutos em anel (fechados),
incluídos na rede de abastecimento de água.
Hidráulico
cálculo da tubulação é reduzido como
geralmente para resolver três problemas principais:
-
definição
fluxo de tubulação Q,
se conhecido
pressão H,
comprimento eu
e diâmetro d
encanamento,
dada a disponibilidade de determinados
resistências ou na sua ausência; -
definição
pressão necessária H,
necessário para garantir um passe
fluxo conhecido Q
por pipeline
comprimento eu
e diâmetro d; -
definição
diâmetro da tubulação d
quando
valores de cabeça conhecidos H,
despesa Q
e comprimento eu.
A vazão do fluido é
onde q > vazão do fluido de projeto, m3/s;
- área da seção viva do tubo, m2.
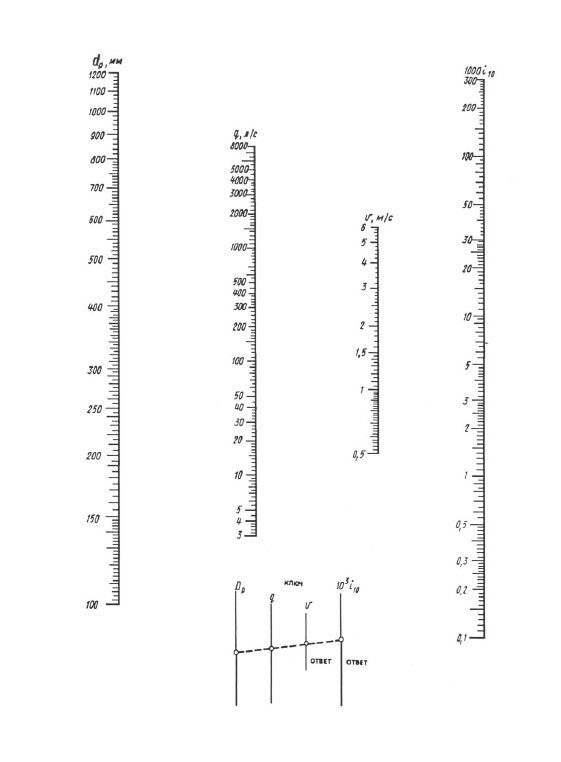
O coeficiente de resistência ao atrito λ é determinado de acordo com os regulamentos do conjunto de regras SP 40-102-2000 “Projeto e instalação de tubulações para sistemas de abastecimento de água e esgoto feitos de materiais poliméricos. Requerimentos gerais":
onde b é algum número de similaridade de regimes de fluxo de fluido; para b > 2, b = 2 é tomado.
onde Re é o número real de Reynolds.
onde ν é o coeficiente de viscosidade cinemática do líquido, m²/s. Ao calcular os tubos de água fria, é considerado igual a 1,31 10-6 m² / s - a viscosidade da água a uma temperatura de +10 ° C;
Rekv > - Número de Reynolds correspondente ao início da região quadrática de resistência hidráulica.
onde Ke é a rugosidade hidráulica do material do tubo, m. Para tubos feitos de materiais poliméricos, Ke = 0,00002 m é tomado se o fabricante do tubo não fornecer outros valores de rugosidade.
Nos casos de vazão em que Re ≥ Rekv, o valor calculado do parâmetro b torna-se igual a 2, e a fórmula (4) é significativamente simplificada, transformando-se na conhecida fórmula de Prandtl:
Em Ke = 0,00002 m, a região de resistência quadrática ocorre a uma vazão de água (ν = 1,31 10-6 m²/s) igual a 32,75 m/s, o que é praticamente inatingível em sistemas públicos de abastecimento de água.
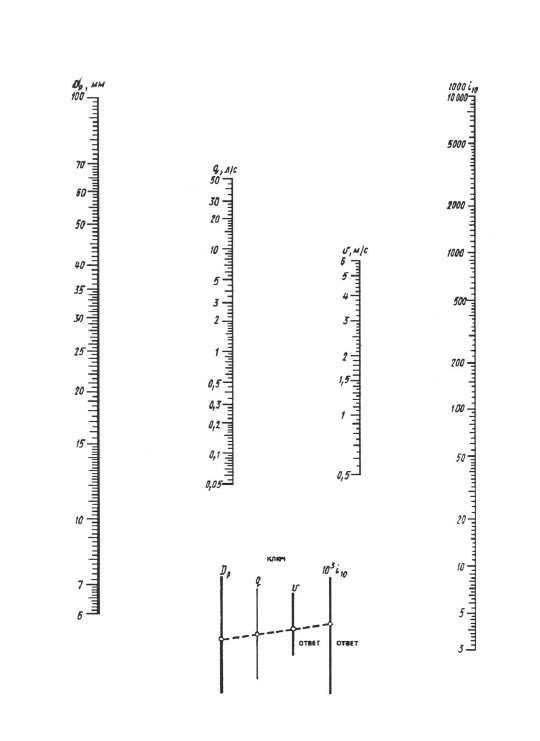
Para cálculos diários, nomogramas são recomendados e para cálculos mais precisos - "Tabelas para cálculos hidráulicos de tubulações feitas de materiais poliméricos", volume 1 "Tubulações de pressão" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
Ao calcular de acordo com nomogramas, o resultado é alcançado por uma sobreposição da régua - você deve conectar o ponto com o valor do diâmetro calculado na escala dp com o ponto com o valor da vazão calculada no q (l / s) escala com linha reta, continuar esta linha reta até cruzar com as escalas de velocidade V e altura de perdas específicas 1000 i (mm/m). Os pontos de intersecção de uma linha reta com essas escalas dão o valor V e 1000 i.
Como você sabe, o custo da eletricidade para bombear o líquido é diretamente proporcional ao valor de H (ceteris paribus). Substituindo a expressão ( 3 ) na fórmula ( 2 ), é fácil ver que o valor de i (e, consequentemente, H) é inversamente proporcional ao diâmetro calculado dp até o quinto grau.
Mostra-se acima que o valor de dp depende da espessura da parede do tubo e: quanto mais fina a parede, maior dp e, consequentemente, menor a perda de pressão por atrito e o custo da eletricidade.
Se o valor MRS do tubo mudar por qualquer motivo, seu diâmetro e espessura de parede (SDR) devem ser recalculados.
Deve-se ter em mente que em alguns casos o uso de tubos com MRS 10 em vez de tubos com MRS 8, especialmente tubos com MRS 6.3, permite reduzir o diâmetro da tubulação em um tamanho. Portanto, em nosso tempo, o uso de polietileno PE 80 (MRS 8) e PE 100 (MRS 10) em vez de polietileno PE 63 (MRS 6.3) para a fabricação de tubos permite não só reduzir a espessura da parede dos tubos, mas também seu peso e consumo de materiais, mas também para reduzir os custos de energia para bombear líquidos (ceteris paribus).
Nos últimos anos (após 2013), os tubos feitos de polietileno PE80 foram quase completamente substituídos da produção por tubos feitos de polietileno grau PE100. Isso se explica pelo fato de as matérias-primas de que são feitos os tubos serem fornecidas do exterior com a marca PE100.E também o fato de o polietileno 100 possuir características de maior resistência, pelo que os tubos são produzidos com as mesmas características dos tubos feitos de PE80, mas com uma parede mais fina, aumentando assim o rendimento dos dutos de polietileno.
Nomograma para determinar as perdas de pressão em tubos com diâmetros de 6, 100 mm.
Nomograma para determinar as perdas de pressão em tubos com diâmetros de 100, 1200 mm.
Critério de Reynolds
Essa dependência foi trazida pelo físico e engenheiro inglês Osborne Reynolds (1842-1912).
O critério que ajuda a responder se há necessidade de levar em conta a viscosidade é o número de Reynolds Re. É igual à razão entre a energia de movimento de um elemento de um fluido em escoamento e o trabalho das forças internas de atrito.
Considere um elemento de fluido cúbico com comprimento de aresta n. A energia cinética de um elemento é:
De acordo com a lei de Newton, a força de atrito que atua sobre um elemento de fluido é definida da seguinte forma:
O trabalho dessa força ao mover um elemento fluido por uma distância n é
e a razão entre a energia cinética do elemento fluido e o trabalho da força de atrito é
Reduzimos e obtemos:
Re é chamado de número de Reynolds.
Assim, Re é uma quantidade adimensional que caracteriza o papel relativo das forças viscosas.
Por exemplo, se as dimensões do corpo com o qual o líquido ou gás está em contato são muito pequenas, mesmo com uma viscosidade pequena, Re será insignificante e as forças de atrito desempenharão um papel predominante. Pelo contrário, se as dimensões do corpo e a velocidade forem grandes, então Re >> 1 e mesmo uma grande viscosidade quase não terão efeito sobre a natureza do movimento.
No entanto, números de Reynolds altos nem sempre significam que a viscosidade não desempenha nenhum papel. Assim, quando um valor muito grande (várias dezenas ou centenas de milhares) do número Re é atingido, um fluxo laminar suave (da lâmina latina - “placa”) se transforma em turbulento (do latim turbulentus - “tempestuosa” , “caótico”), acompanhado por líquidos caóticos, movimentos instáveis. Esse efeito pode ser observado se você abrir gradualmente uma torneira de água: um fluxo fino geralmente flui suavemente, mas com o aumento da velocidade da água, a suavidade do fluxo é perturbada. Em um jato que flui sob alta pressão, as partículas líquidas se movem aleatoriamente, oscilando, todo movimento é acompanhado por uma forte mistura.
O aparecimento de turbulência aumenta muito o arrasto. Em uma tubulação, a velocidade do fluxo turbulento é menor que a velocidade do fluxo laminar nas mesmas quedas de pressão. Mas a turbulência nem sempre é ruim. Devido ao fato de que a mistura durante a turbulência é muito significativa, a transferência de calor - resfriamento ou aquecimento de agregados - ocorre de maneira muito mais intensa; a propagação de reações químicas é mais rápida.
Equação de movimento estacionário de Bernoulli
Uma das equações mais importantes da hidromecânica foi obtida em 1738 pelo cientista suíço Daniel Bernoulli (1700-1782). Ele foi o primeiro a descrever o movimento de um fluido ideal, expresso na fórmula de Bernoulli.
Um fluido ideal é um fluido no qual não há forças de atrito entre os elementos de um fluido ideal, bem como entre o fluido ideal e as paredes do recipiente.
A equação do movimento estacionário que leva seu nome é:
onde P é a pressão do líquido, ρ é sua densidade, v é a velocidade do movimento, g é a aceleração da queda livre, h é a altura na qual o elemento do líquido está localizado.
O significado da equação de Bernoulli é que dentro de um sistema cheio de líquido (seção da tubulação) a energia total de cada ponto permanece sempre inalterada.
A equação de Bernoulli tem três termos:
- ρ⋅v2/2 - pressão dinâmica - energia cinética por unidade de volume do fluido de acionamento;
- ρ⋅g⋅h - pressão de peso - energia potencial por unidade de volume de líquido;
- P - pressão estática, em sua origem é o trabalho das forças de pressão e não representa uma reserva de nenhum tipo especial de energia (“energia de pressão”).
Esta equação explica por que em seções estreitas do tubo a velocidade do fluxo aumenta e a pressão nas paredes do tubo diminui. A pressão máxima nos tubos é definida exatamente no local onde o tubo tem a maior seção transversal. Partes estreitas do tubo são seguras a esse respeito, mas a pressão neles pode cair tanto que o líquido ferve, o que pode levar à cavitação e à destruição do material do tubo.
Equação de Navier-Stokes para líquidos viscosos
Em uma formulação mais rigorosa, a dependência linear do atrito viscoso na mudança na velocidade do fluido é chamada de equação de Navier-Stokes. Ela leva em conta a compressibilidade de líquidos e gases e, diferentemente da lei de Newton, é válida não apenas próximo à superfície de um corpo sólido, mas também em todos os pontos do líquido (próximo à superfície de um corpo sólido no caso de um corpo incompressível). líquido, a equação de Navier-Stokes e a lei de Newton coincidem).
Quaisquer gases para os quais a condição de um meio contínuo é satisfeita também obedecem à equação de Navier-Stokes, ou seja, são fluidos newtonianos.
A viscosidade de líquidos e gases é geralmente significativa em velocidades relativamente baixas, portanto, às vezes se diz que a hidrodinâmica de Euler é um caso especial (limitante) de altas velocidades da hidrodinâmica de Navier-Stokes.
Em baixas velocidades, de acordo com a lei do atrito viscoso de Newton, a força de arrasto do corpo é proporcional à velocidade. Em altas velocidades, quando a viscosidade deixa de desempenhar um papel significativo, a resistência do corpo é proporcional ao quadrado da velocidade (que foi descoberta e fundamentada por Newton).
Sequência de Cálculo Hidráulico
1.
A circulação principal é selecionada
sistema de aquecimento em anel (a maioria
desfavoravelmente localizado no sistema hidráulico
relação). Em beco sem saída de dois tubos
sistemas é um anel que passa por
instrumento inferior do mais remoto e
riser carregado, em tubo único -
através dos mais remotos e carregados
riser.
Por exemplo,
em um sistema de aquecimento de dois tubos com
circulação principal da fiação superior
o anel passará do ponto de aquecimento
através do riser principal, linha de alimentação,
através do riser mais remoto, aquecimento
aparelho de baixo, linha de retorno
ao ponto de aquecimento.
V
sistemas com movimento de água associado em
o anel é tomado como o principal,
passando pelo meio mais
suporte carregado.
2.
O anel de circulação principal se rompe
em parcelas (a parcela é caracterizada
fluxo de água constante e o mesmo
diâmetro). O diagrama mostra
números de seção, seus comprimentos e
cargas. Carga térmica do principal
parcelas é determinado pela soma
cargas térmicas servidas por estes
parcelas. Para selecionar o diâmetro do tubo
duas quantidades são usadas:
a)
determinado fluxo de água;
b)
perdas de pressão específicas aproximadas
para atrito na circulação de projeto
anel RCasar.
Por
Cálculo Rcp
preciso saber o comprimento do principal
anel de circulação e calculado
pressão de circulação.
3.
A circulação calculada
pressão da fórmula
 ,
,
(5.1)
Onde
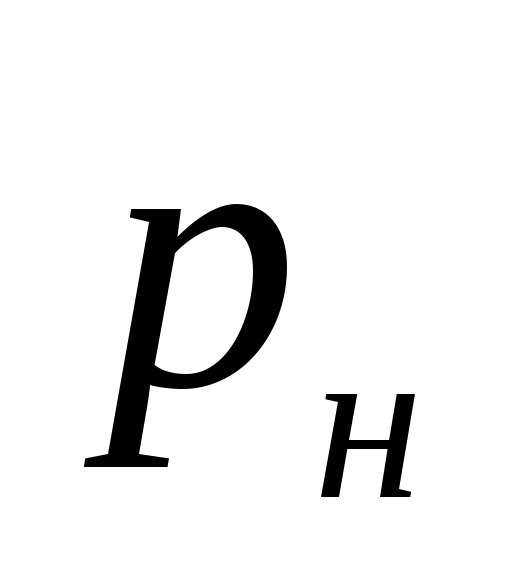
pressão criada pela bomba, Pa.
Prática de Design de Sistema
aquecimento mostrou que o
é aconselhável tomar a pressão da bomba,
igual
 ,
,
(5.2)
Onde
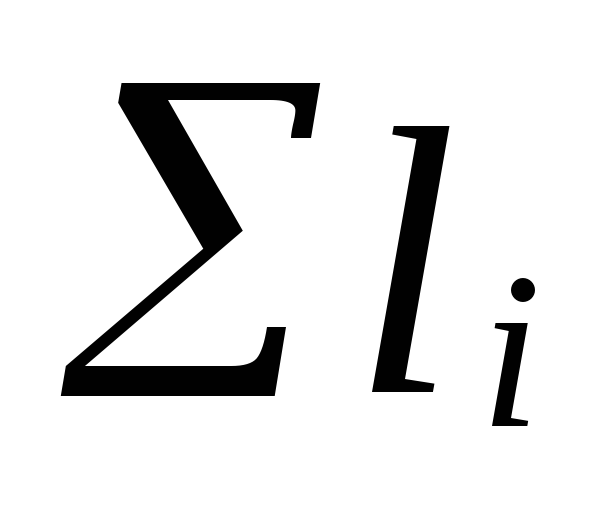
a soma dos comprimentos das seções da circulação principal
argolas;
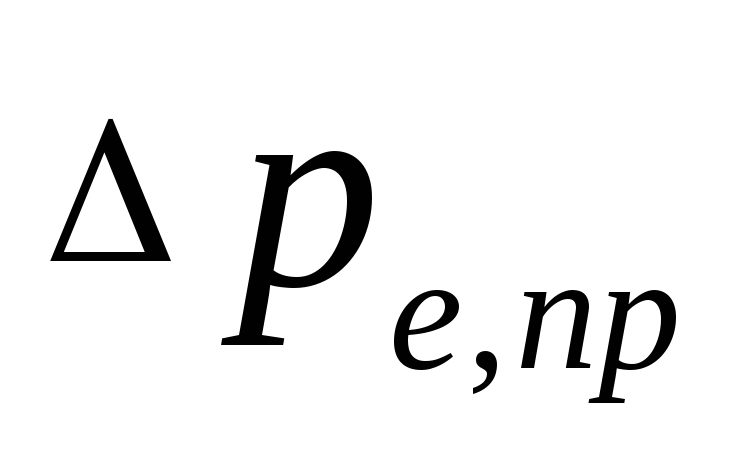
pressão natural que ocorre quando
refrigeração a água em aparelhos, Pa, possível
determinar como
 ,
,
(5.3)
Onde
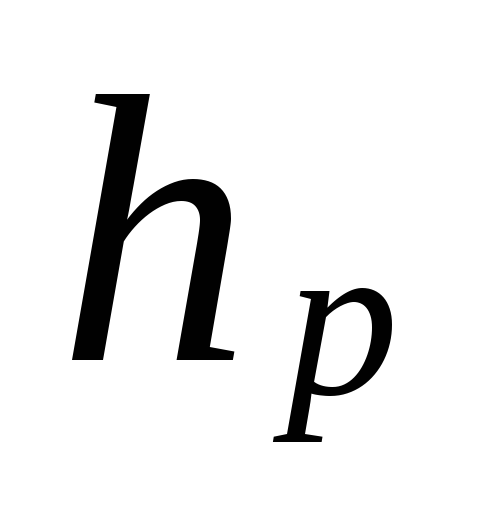
distância do centro da bomba (elevador)
para o centro do dispositivo do piso inferior, m.
Significado
coeficiente possível
determinar a partir da Tabela 5.1.
tabela
5.1 - Significado c
dependendo da temperatura do projeto
água no sistema de aquecimento
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
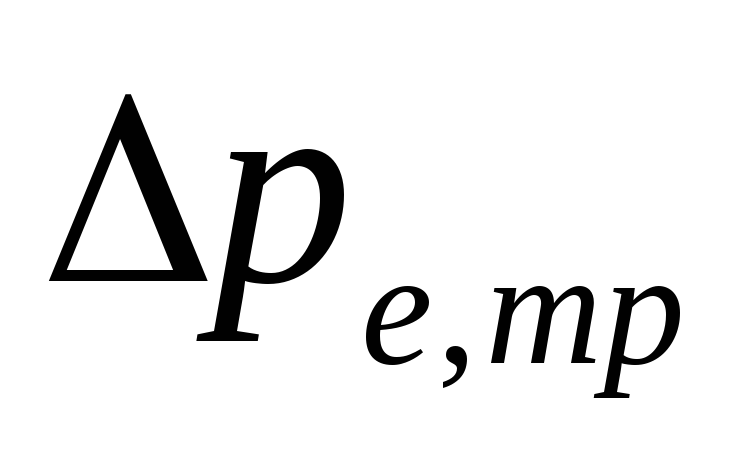
pressão natural em
como resultado do resfriamento a água em tubulações
.
V
sistemas de bombeamento com fiação inferior
magnitude
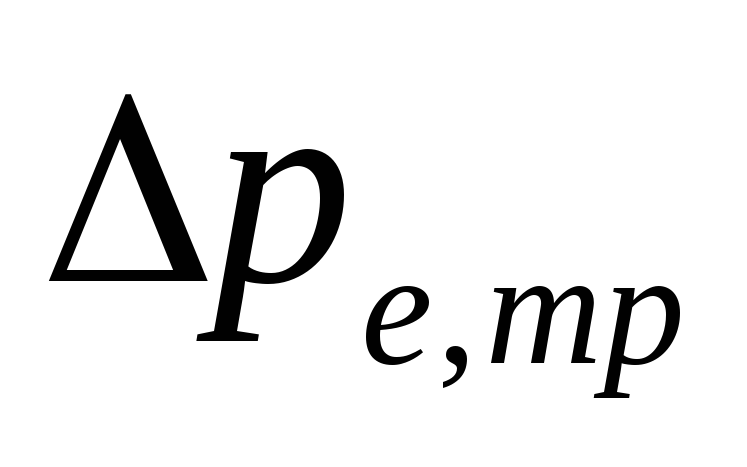
-
Estão determinados
perda de pressão de fricção específica
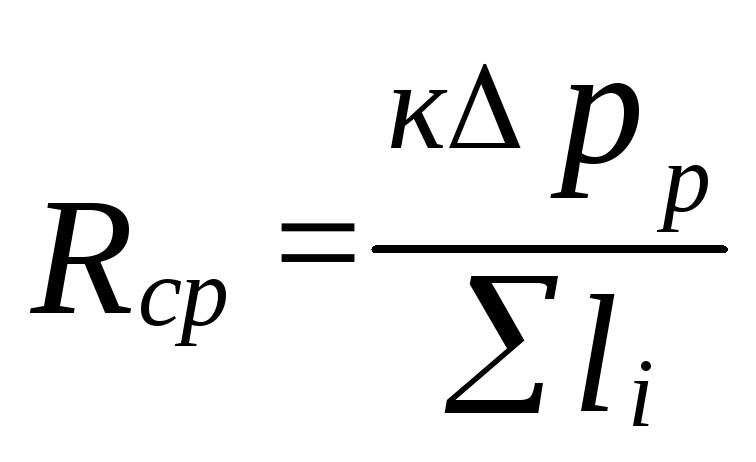
(5.4)
Onde
k=0,65 determina a proporção de perdas de pressão
para atrito.
5.
O consumo de água no local é determinado por
Fórmula
 (5.5)
(5.5)
Onde
Q
- carga de calor no local, W:
(tG
— tO)
- diferença de temperatura do refrigerante.
6.
Por magnitude
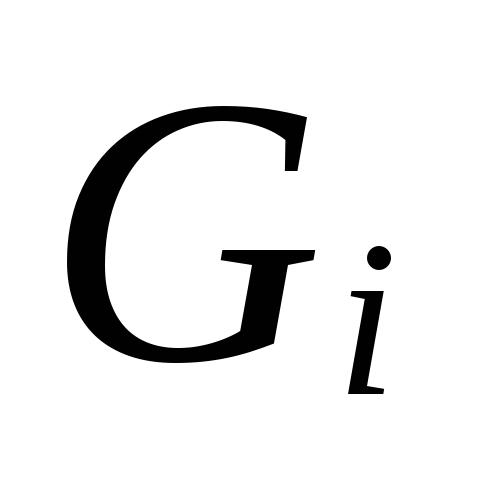
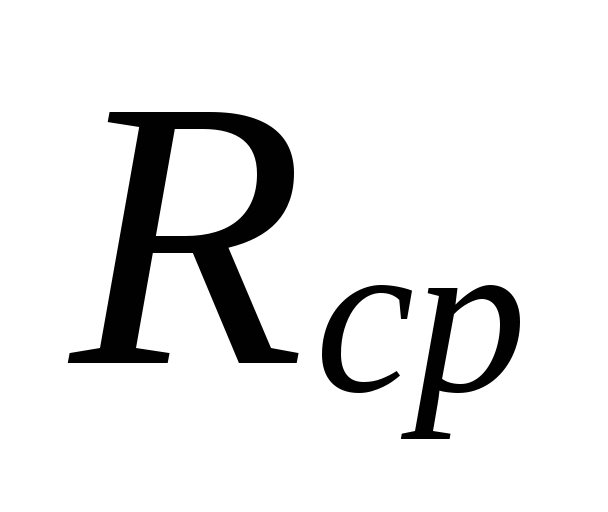
.

6.
Para diâmetros de tubulação selecionados
e o consumo estimado de água é determinado
velocidade do refrigerante v
e o real específico
perda de pressão por atrito Rf.
No
seleção de diâmetros em áreas com pequenas
as taxas de fluxo de refrigerante podem ser
grandes discrepâncias entre
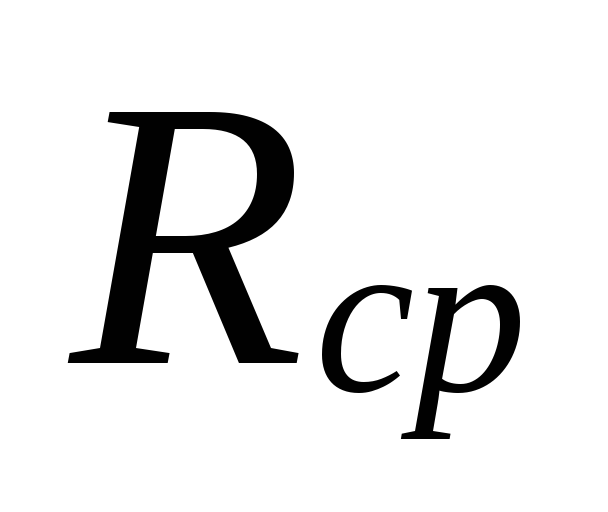
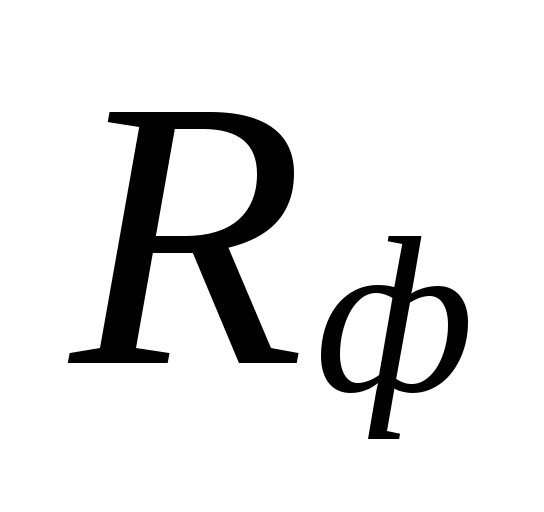
perdas subestimadas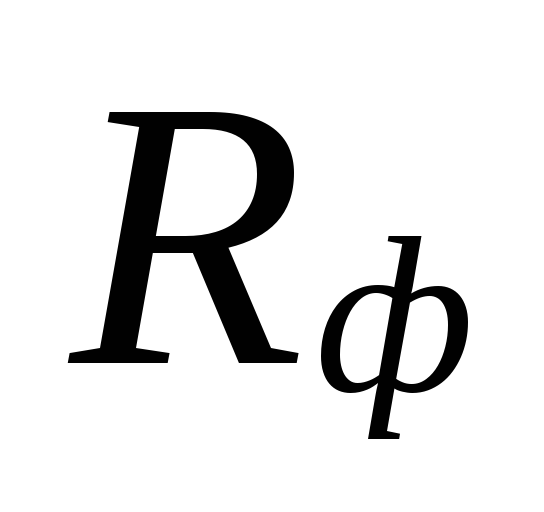
essas áreas são compensadas por uma superestimação
quantidades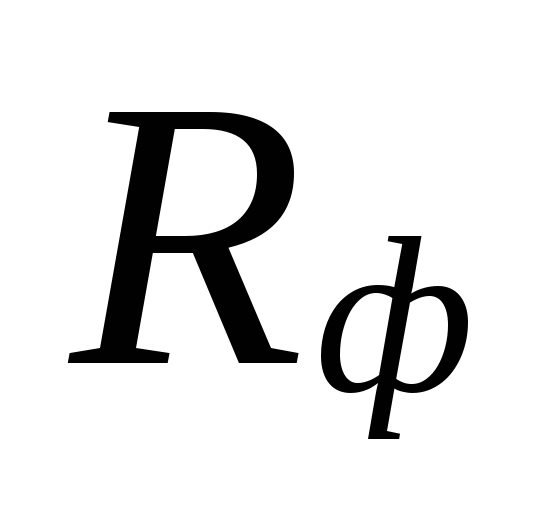
7.
As perdas de pressão de atrito são determinadas
na área calculada, Pa:
 .
.
(5.6)
resultados
os cálculos são inseridos na Tabela 5.2.
8.
Perdas de pressão no local
resistências usando a fórmula:
 ,
,
(5.7)
Onde
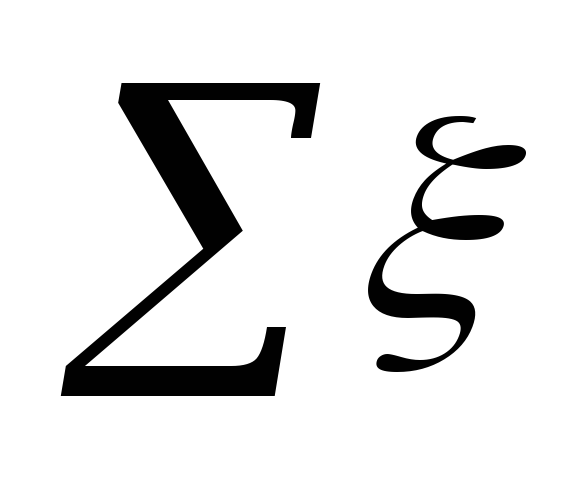
na área de assentamento.
Significado ξ
em cada local estão resumidas na tabela. 5.3.
Tabela 5.3 -
Coeficientes de resistência locais
|
Nº p/p |
Nomes |
Valores |
Notas |
9.
Determine a perda de pressão total
em cada área
 .
.
(5.8)
10. Determinar
perda total de pressão devido ao atrito e
nas resistências locais nas principais
anel de circulação
 .
.
(5.9)
11. Comparar Δр
Com ΔpR.
Perda de pressão total através do anel
deve ser menor que ΔрR
no
 .
.
(5.10)
estoque de descartáveis
pressão é necessária em não contabilizados em
cálculo da resistência hidráulica.
Se as condições não forem
são realizados, é necessário em alguns
seções do anel para alterar os diâmetros dos tubos.
12. Após o cálculo
anel de circulação principal
faça a ligação dos anéis restantes. V
cada novo toque conta apenas
áreas não comuns adicionais,
conectado em paralelo com seções
anel principal.
Discrepância de perda
pressões em paralelo conectado
parcelas permitidas até 15% com um beco sem saída
o movimento da água e até 5% - com passagem.
tabela
5.2 - Resultados do cálculo hidráulico
para sistema de aquecimento
|
No |
Por |
Por |
||||||||||||||
|
Número |
térmico |
Consumo |
Comprimento |
Diâmetro |
Velocidade |
Específico |
Perdas |
Soma |
Perdas |
d, |
v, |
R, |
Δрtr, |
∑ξ |
Z, |
Rl+Z, |
Lição 6
Mudança na temperatura do gás ao longo do comprimento do gasoduto
No fluxo de gás estacionário, a massa
a vazão no gasoduto é
 . (2.41)
. (2.41)
De fato, o movimento do gás no gasoduto
é sempre não isotérmica. V
Durante a compressão, o gás aquece.
Mesmo após seu resfriamento no COP, a temperatura
gás que entra no gasoduto
é de cerca de 2040С,
que é muito superior à temperatura
ambiente (T).
Na prática, a temperatura do gás torna-se
perto da temperatura ambiente
apenas para gasodutos de pequeno diâmetro
(Dy0.
Além disso, deve-se levar em conta que
gás canalizado
é um gás real, que é inerente
o efeito Joule-Thompson, que leva em conta
absorção de calor durante a expansão do gás.
Quando a temperatura muda ao longo do comprimento
o movimento do gás do gasoduto é descrito
sistema de equações:
energia especifica ,
,
continuidade ,
,
estados ,
,
equilíbrio térmico .
.
Considere na primeira aproximação a equação
balanço térmico sem levar em conta o efeito
Joule Thompson. Integrando a equação
equilíbrio térmico
 ,
,
Nós temos
 , (2.42)
, (2.42)
Onde ;
;
KSR- média no site cheio
coeficiente de transferência de calor do gás para
ambiente;
G é a vazão mássica de gás;
cP–
capacidade térmica isobárica média do gás.
um valortL é chamado de critério adimensional
Shukhov
 (2.43)
(2.43)
Então a temperatura do gás no final
gasoduto será
 . (2.44)
. (2.44)
A uma distância x do início
a temperatura do gás do gasoduto é determinada
de acordo com a fórmula
 . (2.45)
. (2.45)
Mudança de temperatura ao longo do comprimento do gasoduto
é exponencial (Fig.
2.6).
Considerar
efeito da mudança de temperatura do gás sobre
desempenho da tubulação.
Multiplicando ambos os lados da equação específica
energia em 2 e expressando ,
,
Nós temos
 . (2.46)
. (2.46)
Expressamos a densidade do gás no lado esquerdo
expressões (2.46) da equação de estado
 ,
,
produtow da equação de continuidade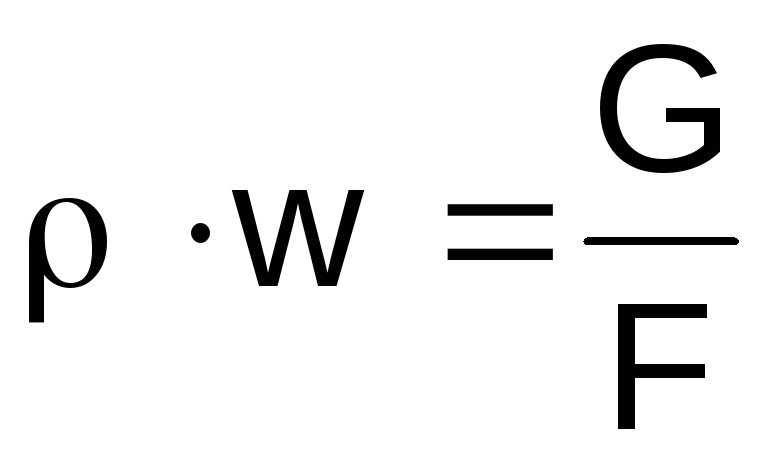
Saldo .
.
Com isso em mente, a equação específica
energia toma a forma
 (2.47)
(2.47)
ou
 . (2.48)
. (2.48)
denotando
 e integrando o lado esquerdo da equação
e integrando o lado esquerdo da equação
(2,48) de PHdoPPARA, e à direita de THpontoPARA, Nós temos
 . (2.49)
. (2.49)
Ao substituir
 , (2.50)
, (2.50)
temos
 . (2.51)
. (2.51)
Depois de integrar no especificado
limites, obtemos

 . (2.52)
. (2.52)
Levando em conta (2,42)

ou
 , (2.53)
, (2.53)
Onde é um fator de correção que leva em consideração
é um fator de correção que leva em consideração
mudança de temperatura ao longo do comprimento do gasoduto
(não isotermalidade do fluxo de gás).
Levando em conta (2.53), a dependência para determinar
vazão mássica de gás terá a forma
 . (2.54)
. (2.54)
Valor Hsempre maior que um, então
vazão mássica de gás ao mudar
temperatura ao longo do comprimento do gasoduto
(regime de fluxo não isotérmico) sempre
menos do que no modo isotérmico
(T=idem). Produto THé chamada de integral média
temperatura do gás na tubulação.
Com os valores do número Shukhov Shu4
fluxo de gás na tubulação
considere quase isotérmica
em T=idem. tal temperatura
é possível ao bombear gás com
baixo custo do gasoduto
diâmetro pequeno (menos de 500 mm) para um
distância.
Efeito da mudança de temperatura do gás
manifesta-se pelos valores do número Shukhov
Shu
No
gás bombeando a presença de um acelerador
efeito leva a um profundo
refrigeração a gás do que apenas com troca de calor
com solo. Neste caso a temperatura
o gás pode até cair abaixo
temperatura T (Fig.
2.7).
Arroz. 2.7. Influência do efeito Joule-Thompson
na distribuição da temperatura do gás
comprimento da tubulação
1 - sem levar em conta Di; 2 - com
levando em conta Di
Então, levando em conta o coeficiente Joule-Thompson
lei da mudança de temperatura ao longo do comprimento
toma a forma
 , (2.55)
, (2.55)
5 Perdas hidráulicas
Diferença
pressão do óleo em duas seções de um
e o mesmo gasoduto, desde que
o primeiro está localizado a montante, e
o segundo - abaixo, é determinado equação
Bernoulli
 ,
,
Onde
h2
– h1
- a diferença nas alturas dos centros de gravidade
seções de uma escolha arbitrária
nível horizontal;
v1,
v2
– velocidades médias do óleo nos trechos;
g - aceleração da força
gravidade;

perdas hidráulicas durante o movimento
óleos da primeira seção para a segunda.
A equação
Bernoulli em pleno uso
para cálculo de linhas de sucção de bombas;
em outros casos, o primeiro termo,
geralmente negligenciado e considerado:

hidráulico
as perdas são geralmente divididas em
perdas e perdas por atrito ao longo do comprimento
tubulações (linear).
1.5.1
perdas locais
energias são devidas a
resistência hidráulica,
causando distorção do fluxo. Local
resistências são: constrições,
expansão, arredondamento de tubulações,
filtros, equipamentos de controle e
regulamento, etc. Ao fluir
líquidos através de resistências locais
sua velocidade muda e geralmente há
grandes vórtices.
Perdas
pressão das resistências locais
determinado pela fórmula Weisbach:
 MPa
MPa
(ou
 Pa),
Pa),
Onde

perda,
v
é a velocidade média do fluxo ao longo da seção transversal
em um tubo atrás da resistência local, m/s;
,
N/m3;
g=9,81 m/s2.
Cada
resistência local é caracterizada
pelo seu valor de coeficiente

Com fluxo turbulento, os valores
resistência e mudar muito pouco
com uma mudança no tamanho da seção, velocidade
fluidez e viscosidade do fluido. assim
assumir que eles não dependem do número
Reynolds R.
Valores

por exemplo, para camisetas com o mesmo
diâmetros de canal são tomados iguais,
E se:
fluxos
somar, divergir; fluxo
passagem;









no
curva do tubo

Valores

em sistemas hidráulicos de equipamentos, retirados de
literatura de referência.
No
fluxo laminar (Re
Perdas
pressão de resistências locais em
fluxo laminar são determinados por
Fórmula:
 MPa
MPa
Onde

= a

Quantidades
perda de pressão no padrão
dispositivos hidráulicos para
vazão nominal geralmente
listados em suas especificações técnicas.
1.5.2
Perda em
atrito de comprimento
é a perda de energia que ocorre
em tubos retos de seção transversal constante,
Essa. com fluxo de fluido uniforme,
e aumenta proporcionalmente ao comprimento
tubos. Essas perdas são devidas a problemas internos
atrito em um líquido e, portanto, têm
coloque em tubos ásperos e lisos.
Perdas
pressão de atrito da tubulação
é determinado pela fórmula Darcy:
 MPa
MPa
Onde

eu
e d
- comprimento e diâmetro interno da tubulação,
milímetros.
Isto
a fórmula é aplicável tanto para laminar,
bem como em fluxo turbulento; diferença
consiste apenas nos valores do coeficiente

No
fluxo laminar (Re
No
coeficiente de atrito de fluxo turbulento
não é apenas uma função de Re, mas
também depende da rugosidade do interior
superfície do tubo. Por hidraulicamente
suave tubos,
Essa. com uma aspereza que
praticamente não afeta sua resistência,
coeficiente de atrito turbulento
modo pode ser determinado pela fórmula computador.
Konakova:

tubo
é considerado hidraulicamente suave se
(d/k)>(Re/20),
onde k é a rugosidade equivalente,
milímetros. Por exemplo, para novos aços sem costura
tubos k≈0,03
mm, e após vários anos de operação
k≈0,2
mm, para novos tubos sem costura feitos de
metais não ferrosos k≈0,005
milímetros. Estes tubos são frequentemente utilizados em
sistemas hidráulicos de máquinas-ferramentas.
Coeficiente
atrito no regime turbulento pode ser
determinar pela fórmula Altshulya,
sendo universal (ou seja, aplicável
em qualquer caso):

2. Características de fluxo do módulo de fluxo de tubulação
Vamos lembrar
fórmula de perda linear - fórmula de Darcy
- Weisbach:
 .
.
Expressar
nesta fórmula, a velocidade V
através do fluxo Q
da proporção
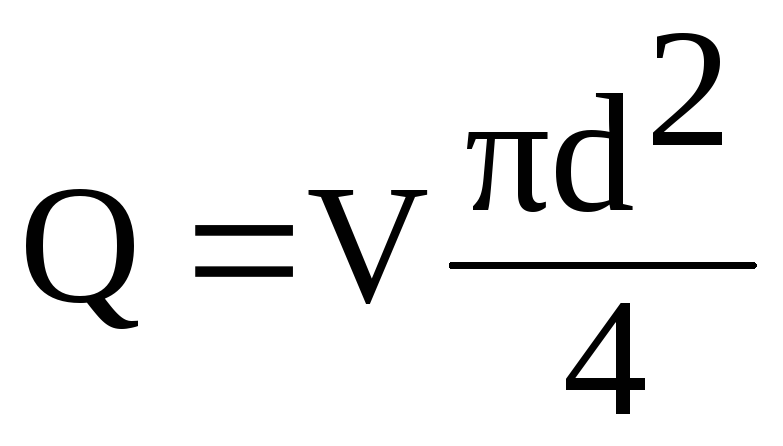
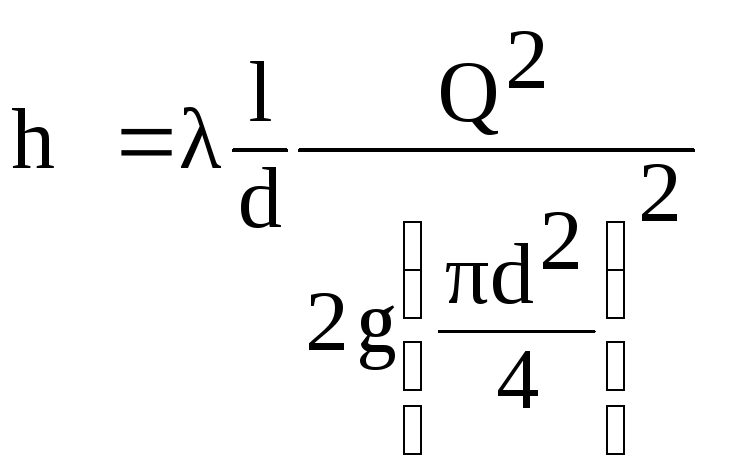
(6.1)
Por
tubulação de um determinado diâmetro
complexo de quantidades
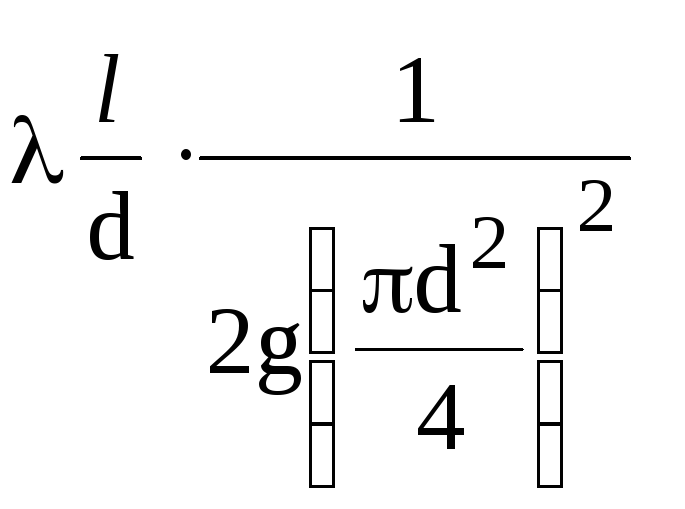
constante (1/K2),
exceto para o coeficiente hidráulico
atrito λ. Baseado no conceito
velocidade econômica média Vs.e
vamos mostrar que o coeficiente indicado λ
pode ser atribuído a este complexo, porque v
Neste caso, o número de Reynolds será
tem um significado específico:
 ,
,
e no gráfico de Nikuradze, o coeficiente λ em
este caso terá um
significado.
Justificar
legitimidade de introduzir o conceito
velocidade econômica média da seguinte forma
raciocínio.
hidráulico
sistema, como encanamento,
você pode pular uma certa despesa
feitos de tubos de diferentes diâmetros. No
Ao mesmo tempo, com o aumento do diâmetro d,
portanto, uma diminuição na velocidade V
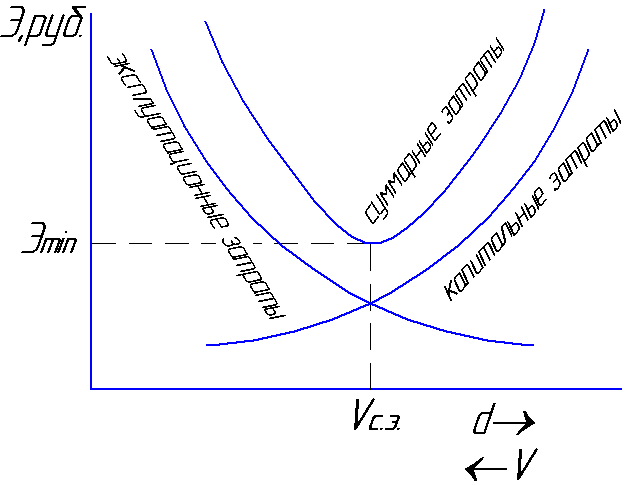
as despesas de capital aumentarão, e
os custos operacionais serão
diminuir devido a uma diminuição do fluxo hidráulico
perdas. A velocidade com que o total
os custos serão mínimos
será chamado de economia média
velocidade Vs.e
= 0,8 ... 1,3 m/s (Fig. 6.1).
fig.6.1
Então
a fórmula de perda linear (6.1) assume a forma
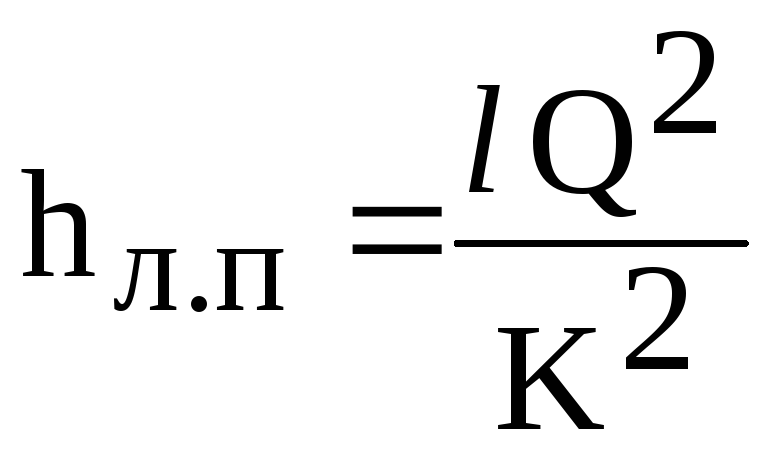
(6.2)
Onde
K - característica de fluxo da tubulação
(módulo de fluxo), dependente do material
tubulação, diâmetro e vazão. é levado
das mesas.
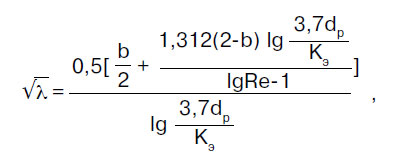
 ),C
),C ,
,