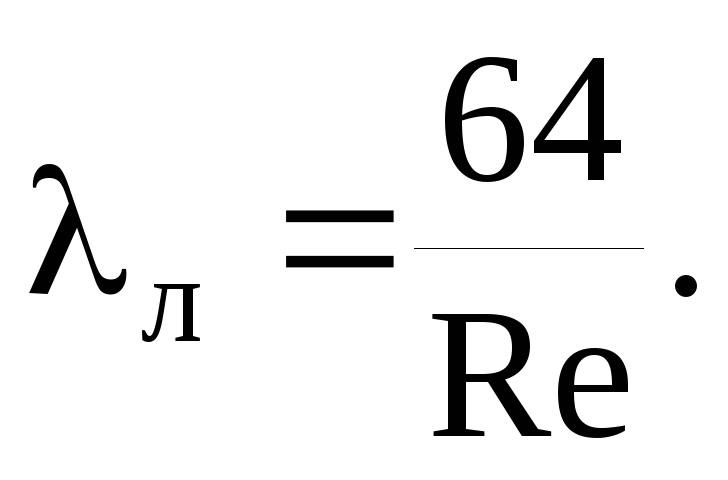1. Hydrostatický tlak
Hydrostatický tlak je
vnitřní tlaková síla v důsledku
působením vnějších sil působících na
daný bod v kapalině. Takový tlak
ve všech směrech je stejný a závisí
na pozici bodu v kapalině v klidu.
Dimenze hydrostatického tlaku
v systému MKGSS - kg / cm2 nebo t / m2,
v soustavě SI - N/m2.
Základní jednotkové poměry
tlak:
|
kg/cm2 |
N/m2 |
|
|
technická atmosféra |
1 |
98066,5 |
|
milimetr vodního sloupce |
0,0001 |
9,80665 |
|
milimetr rtuti |
0,00136 |
133,32 |
V praktických výpočtech 1 technický
atmosféra \u003d 1 kg / cm2 \u003d 10 m vody. Umění. =
735 mmHg Umění. = 98070 N/m2.
Tedy pro nestlačitelnou tekutinu
v rovnováze pod silou
gravitační, plně hydrostatické
bodový tlak:
p=p+

kde p je tlak na volné
povrch kapaliny;

výška h s plochou
průřez rovný jedné;
h - hloubka ponoru
body;

U některých kapalin hodnoty
měrná hmotnost použitá při řešení
úkoly jsou uvedeny v příloze (tab.
P-3).
Hodnota přetlaku nad
atmosférický (strA)
tzv. manometrická, popř
přetlak:

Pokud tlak na volnou plochu
rovná se atmosférickému, pak přebytečnému
tlak pm=

Podatmosférický tlak
množství se nazývá vakuum:
Rcvok= pA- R.
Řešení většiny těchto problémů
sekce souvisí s použitím
základní rovnice hydrostatiky

kde z je souřadnice nebo
bodová značka.
1. Obecné informace o hydraulickém výpočtu potrubí
Při počítání
potrubí, která se zvažují
stálý, rovnoměrný tlak
pohyb jakékoli tekutiny
turbulentního režimu, v kruhově válcovém
potrubí. Kapalina v tlakovém potrubí
je pod tlakem a
jejich průřezy jsou zcela
naplněné. Pohyb tekutiny podél
v důsledku toho vzniká potrubí
skutečnost, že tlak na jeho začátku je větší než
na konci.
Hydraulické
výpočet se provádí za účelem určení
průměr potrubí d
se známým
délka pro zajištění přeskočení
určitý průtok Q
nebo založení
při daném průměru a délce požadované
tlak a průtok kapaliny. Potrubí
v závislosti na jejich délce a vzoru
lokality jsou rozděleny na jednoduché
a komplexní. K jednoduchým potrubím
zahrnuje potrubí, která nemají
větve po délce, s konstantou
stejný náklad.
Potrubí
sestávají z trubek stejného průměru
po celé délce nebo z různých částí potrubí
průměry a délky. Poslední případ
odkazuje na sériové připojení.
Jednoduché potrubí
v závislosti na délce s pozemkem místní
odpory se dělí na krátké a
dlouho. krátký
potrubí
jsou
potrubí dostatečně krátké délky,
ve kterém místní odpor
tvoří více než 10 % hydrauliky
ztráta délky. Patří mezi ně například:
sifonové trubky, sání
potrubí lamelových čerpadel, sifonů (tlak
vodovodní potrubí pod silničním náspem),
potrubí uvnitř budov a konstrukcí
atd.
dlouho
potrubí
volala
potrubí jsou poměrně velká
délky, ve kterých dochází ke ztrátě hlavy po délce
výrazně převyšují místní
ztráty. Místní ztráty jsou
méně než 5
ztráty po délce potrubí, a proto
mohou být zanedbány nebo zavedeny na
hydraulické výpočty se zvyšují
koeficient rovný 1,05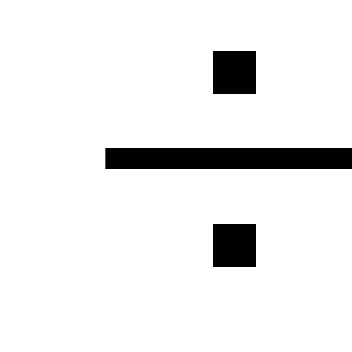
Do systému vstupují dlouhé potrubí
vodovodní sítě, čerpací potrubí
stanice, potrubí a potrubí
průmyslové podniky a
zemědělský účel a
atd.
Složité potrubí
mít různé větve po délce,
ty. potrubí se skládá ze sítě potrubí
určité průměry a délky. Komplex
potrubí se dělí na
paralelní, slepá (rozvětvená),
prstencové (uzavřené) potrubí,
součástí vodovodní sítě.
Hydraulické
výpočet potrubí je snížen jako
obvykle řeší tři hlavní problémy:
-
definice
tok potrubí Q,
je-li známo
tlak H,
délka l
a průměr d
potrubí,
vzhledem k dostupnosti některých místních
odpory nebo v jejich nepřítomnosti; -
definice
požadovaný tlak H,
nutné k zajištění propustky
známý tok Q
potrubím
dlouho l
a průměr d; -
definice
průměr potrubí d
když
známé hodnoty hlavy H,
výdaj Q
a délka l.
Rychlost proudění tekutiny je
kde q > návrhový průtok kapaliny, m3/s;
- plocha živé části potrubí, m2.
Součinitel třecího odporu λ je stanoven v souladu s předpisy souboru pravidel SP 40-102-2000 „Projektování a montáž potrubí pro vodovody a kanalizace z polymerních materiálů. Obecné požadavky":
kde b je určitý počet podobností režimů proudění tekutiny; pro b > 2 se bere b = 2.
kde Re je skutečné Reynoldsovo číslo.
kde ν je koeficient kinematické viskozity kapaliny, m²/s. Při výpočtu potrubí studené vody se bere jako 1,31 10-6 m² / s - viskozita vody při teplotě +10 ° C;
Rekv > - Reynoldsovo číslo odpovídající začátku kvadratické oblasti hydraulického odporu.
kde Ke je hydraulická drsnost materiálu trubky, m. Pro trubky vyrobené z polymerních materiálů se bere Ke = 0,00002 m, pokud výrobce trubky neudává jiné hodnoty drsnosti.
V těch případech průtoku, kdy Re ≥ Rekv, se vypočtená hodnota parametru b rovná 2 a vzorec (4) je výrazně zjednodušen a přechází do známého Prandtlova vzorce:
Při Ke = 0,00002 m se oblast kvadratického odporu vyskytuje při průtoku vody (ν = 1,31 10-6 m²/s) rovném 32,75 m/s, což je ve veřejných vodovodních sítích prakticky nedosažitelné.
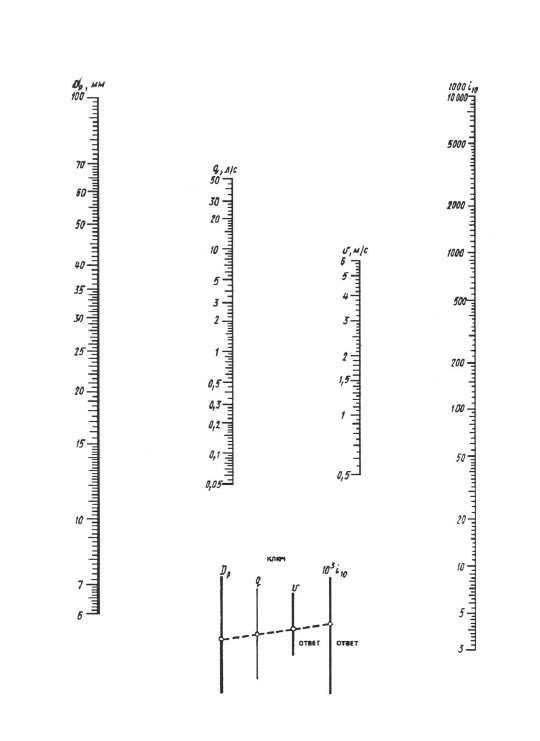
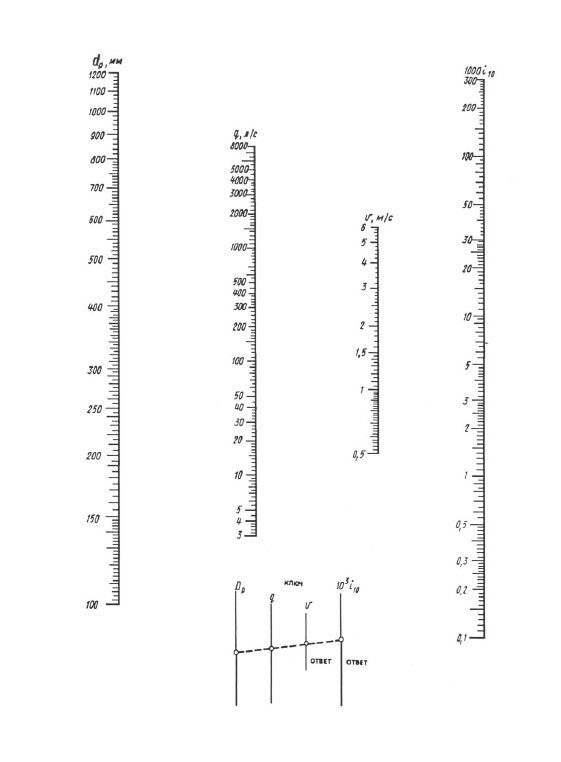
Pro každodenní výpočty se doporučují nomogramy a pro přesnější výpočty - "Tabulky pro hydraulické výpočty potrubí vyrobených z polymerních materiálů", svazek 1 "Tlaková potrubí" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
Při výpočtu podle nomogramů je výsledek dosažen jedním překrytím pravítka - měli byste spojit bod s hodnotou vypočteného průměru na stupnici dp s bodem s hodnotou vypočteného průtoku na q (l / s) stupnice s přímkou, pokračujte v této přímce, dokud se neprotne se stupnicí rychlosti V a měrné ztráty 1000 i (mm/m). Průsečíky přímky s těmito stupnicemi dávají hodnotu V a 1000 i.
Jak víte, náklady na elektřinu na čerpání kapaliny jsou přímo úměrné hodnotě H (ceteris paribus). Dosazením výrazu ( 3 ) do vzorce ( 2 ) je snadné vidět, že hodnota i (a následně H) je nepřímo úměrná vypočtenému průměru dp do pátého stupně.
Výše je ukázáno, že hodnota dp závisí na tloušťce stěny trubky e: čím tenčí je stěna, tím vyšší je dp, a tím nižší je tlaková ztráta v důsledku tření a náklady na elektřinu.
Pokud se hodnota MRS trubky z jakéhokoli důvodu změní, je nutné její průměr a tloušťku stěny (SDR) přepočítat.
Je třeba mít na paměti, že v řadě případů použití trubek s MRS 10 místo trubek s MRS 8, zejména trubek s MRS 6.3, umožňuje zmenšit průměr potrubí o jednu velikost. Proto v naší době použití polyethylenu PE 80 (MRS 8) a PE 100 (MRS 10) místo polyethylenu PE 63 (MRS 6.3) pro výrobu trubek umožňuje nejen snížit tloušťku stěny trubek, ale i jejich hmotnost. a spotřeby materiálu, ale také ke snížení energetických nákladů na čerpání kapaliny (ceteris paribus).
V posledních letech (po roce 2013) byly trubky z polyetylenu PE80 z výroby téměř zcela nahrazeny trubkami z polyetylenu jakosti PE100. Vysvětluje to skutečnost, že suroviny, ze kterých jsou trubky vyrobeny, jsou dodávány ze zahraničí se značkou PE100.A také tím, že polyetylen 100 má vyšší pevnostní charakteristiky, díky čemuž se vyrábí trubky se stejnými vlastnostmi jako trubky z PE80, ale s tenčí stěnou, čímž se zvyšuje průchodnost polyetylenových potrubí.
Nomogram pro stanovení tlakových ztrát v potrubí o průměru 6 100 mm.
Nomogram pro stanovení tlakových ztrát v potrubí o průměrech 100, 1200 mm.
Reynoldsovo kritérium
Tuto závislost přinesl anglický fyzik a inženýr Osborne Reynolds (1842-1912).
Kritériem, které pomáhá odpovědět na otázku, zda je potřeba brát v úvahu viskozitu, je Reynoldsovo číslo Re. Je rovna poměru energie pohybu prvku proudící tekutiny k práci sil vnitřního tření.
Uvažujme kubický fluidní prvek s délkou hrany n. Kinetická energie prvku je:
Podle Newtonova zákona je třecí síla působící na tekutý prvek definována takto:
Práce této síly při pohybu tekutého prvku na vzdálenost n je
a poměr kinetické energie fluidního prvku k práci třecí síly je
Snížíme a získáme:
Re se nazývá Reynoldsovo číslo.
Re je tedy bezrozměrná veličina, která charakterizuje relativní roli viskózních sil.
Pokud jsou například rozměry tělesa, se kterým je kapalina nebo plyn v kontaktu, velmi malé, pak i při nízké viskozitě bude Re nevýznamné a převládající roli hrají třecí síly. Naopak, pokud jsou rozměry tělesa a rychlost velké, pak Re >> 1 a ani velká viskozita nebude mít na charakter pohybu téměř žádný vliv.
Ne vždy velká Reynoldsova čísla však znamenají, že viskozita nehraje žádnou roli. Takže když je dosaženo velmi velké (několik desítek nebo stovek tisíc) hodnoty Re čísla, plynulé laminární (z latinského lamina - "deska") se změní na turbulentní (z latinského turbulentus - "bouřlivý" , „chaotický“), doprovázený chaotickými, nestabilními pohyby kapalin. Tento efekt lze pozorovat, pokud postupně otevíráte vodovodní kohoutek: tenký pramínek obvykle teče plynule, ale se zvyšováním rychlosti vody je plynulost toku narušena. V proudu vytékajícím pod vysokým tlakem se částice kapaliny pohybují náhodně, oscilují, veškerý pohyb je doprovázen silným mícháním.
Vznik turbulence značně zvyšuje odpor vzduchu. V potrubí je rychlost turbulentního proudění menší než rychlost laminárního proudění při stejných tlakových spádech. Turbulence ale nejsou vždy špatné. Vzhledem k tomu, že míchání při turbulenci je velmi výrazné, dochází k přenosu tepla - ochlazování nebo ohřevu agregátů - mnohem intenzivněji; chemické reakce se šíří rychleji.
Bernoulliho rovnice stacionárního pohybu
Jednu z nejdůležitějších rovnic hydromechaniky získal v roce 1738 švýcarský vědec Daniel Bernoulli (1700-1782). Poprvé se mu podařilo popsat pohyb ideální tekutiny, vyjádřený v Bernoulliho vzorci.
Ideální tekutina je tekutina, ve které nejsou žádné třecí síly mezi prvky ideální tekutiny, stejně jako mezi ideální tekutinou a stěnami nádoby.
Rovnice stacionárního pohybu, která nese jeho jméno, je:
kde P je tlak kapaliny, ρ je její hustota, v je rychlost pohybu, g je zrychlení volného pádu, h je výška, ve které se prvek kapaliny nachází.
Význam Bernoulliho rovnice je ten, že uvnitř systému naplněného kapalinou (část potrubí) je celková energie každého bodu vždy nezměněna.
Bernoulliho rovnice má tři členy:
- ρ⋅v2/2 - dynamický tlak - kinetická energie na jednotku objemu hnací kapaliny;
- ρ⋅g⋅h - hmotnostní tlak - potenciální energie jednotkového objemu kapaliny;
- P - statický tlak, ve svém původu je dílem tlakových sil a nepředstavuje rezervu žádného zvláštního druhu energie („tlaková energie“).
Tato rovnice vysvětluje, proč se v úzkých úsecích potrubí zvyšuje rychlost proudění a snižuje se tlak na stěny potrubí. Maximální tlak v potrubí je nastaven přesně v místě, kde má potrubí největší průřez. Úzké části potrubí jsou v tomto ohledu bezpečné, ale tlak v nich může klesnout natolik, že se kapalina vaří, což může vést ke kavitaci a destrukci materiálu potrubí.
Navier-Stokesova rovnice pro viskózní kapaliny
V přesnější formulaci se lineární závislost viskózního tření na změně rychlosti tekutiny nazývá Navier-Stokesova rovnice. Bere v úvahu stlačitelnost kapalin a plynů a na rozdíl od Newtonova zákona platí nejen v blízkosti povrchu pevného tělesa, ale také v každém bodě kapaliny (v případě nestlačitelného tělesa v blízkosti povrchu pevného tělesa). kapalina, Navier-Stokesova rovnice a Newtonův zákon se shodují).
Jakékoli plyny, pro které je splněna podmínka spojitého média, se také řídí Navier-Stokesovou rovnicí, tj. jsou newtonské tekutiny.
Viskozita kapalin a plynů je obvykle významná při relativně nízkých rychlostech, proto se někdy říká, že Eulerova hydrodynamika je zvláštním (limitním) případem vysokých rychlostí Navier-Stokesovy hydrodynamiky.
Při nízkých rychlostech, v souladu s Newtonovým zákonem o viskózním tření, je odporová síla tělesa úměrná rychlosti. Při vysokých rychlostech, kdy viskozita přestává hrát významnou roli, je odpor tělesa úměrný druhé mocnině rychlosti (což jako první objevil a doložil Newton).
Hydraulická výpočtová sekvence
1.
Je vybrán hlavní oběh
kruhový topný systém (většina
nevýhodně umístěný v hydr
vztah). Ve slepé dvoutrubce
systémy je prstenec procházející skrz
spodní nástroj nejvzdálenějších a
zatížená stoupačka, v jedné trubce -
přes nejvzdálenější a nabité
stoupačka.
Například,
ve dvoutrubkovém topném systému s
horní vedení hlavní cirkulace
kroužek projde z bodu zahřívání
přes hlavní stoupačku, přívodní vedení,
přes nejvzdálenější stoupačku, topení
spotřebič v přízemí, zpětné vedení
do bodu ohřevu.
PROTI
systémy se souvisejícím pohybem vody v
prsten je brán jako hlavní,
procházející nejvíce středem
naložený stojan.
2.
Rozbije se hlavní cirkulační kroužek
do parcel (zápletka je charakterizována
konstantní průtok vody a to samé
průměr). Diagram ukazuje
čísla úseků, jejich délky a term
zatížení. Tepelné zatížení hlavní
parcel se určí součtem
tepelná zátěž, kterou obsluhují
zápletky. Pro výběr průměru potrubí
používají se dvě množství:
A)
daný průtok vody;
b)
přibližné specifické tlakové ztráty
pro tření v návrhovém oběhu
prsten RSt.
Pro
výpočet Rcp
potřebujete znát délku hlavní
oběhový kroužek a vypočítané
cirkulační tlak.
3.
Vypočítaný oběh
tlak formule
 ,
,
(5.1)
kde
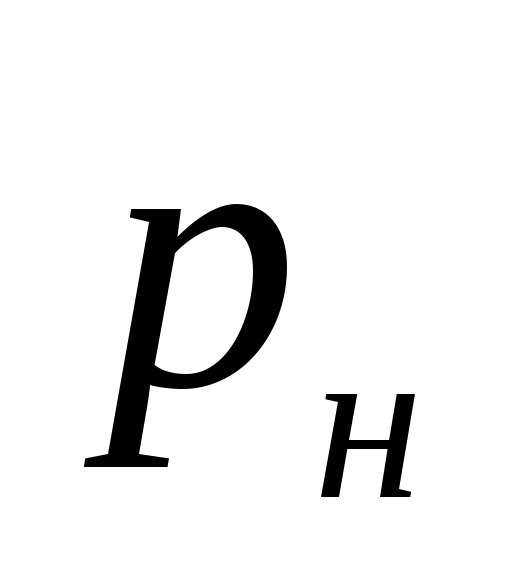
tlak vytvářený čerpadlem, Pa.
Praxe návrhu systému
vytápění ukázalo, že nejvíce
je vhodné měřit tlak čerpadla,
rovnat se
 ,
,
(5.2)
kde
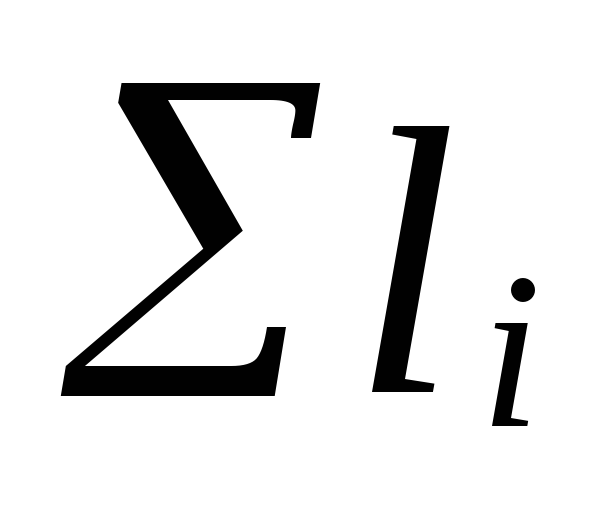
součet délek úseků hlavního oběhu
prsteny;
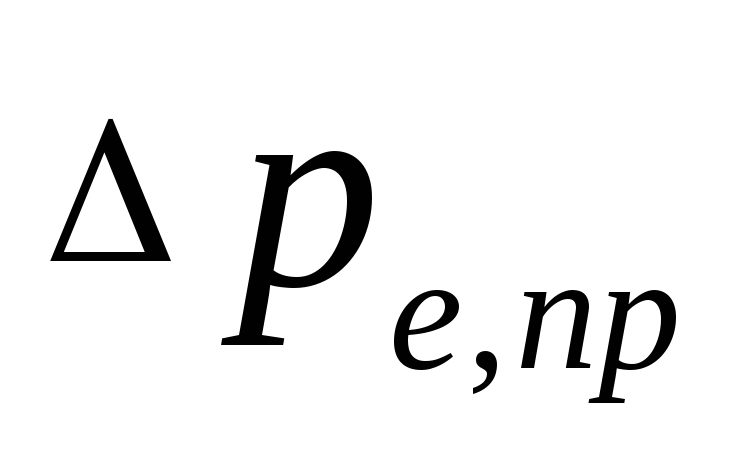
přirozený tlak, ke kterému dochází, když
vodní chlazení ve spotřebičích, Pa, možné
určit jak
 ,
,
(5.3)
kde
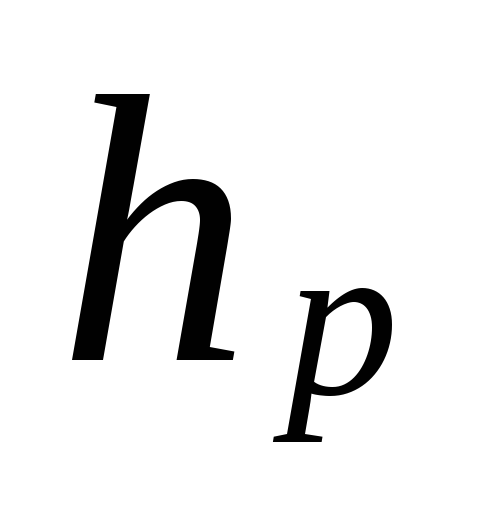
vzdálenost od středu čerpadla (výtahu)
do středu zařízení spodního patra, m.
Význam
součinitel možné
určit z tabulky 5.1.
stůl
5.1 - Význam c
v závislosti na projektované teplotě
vody v topném systému
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
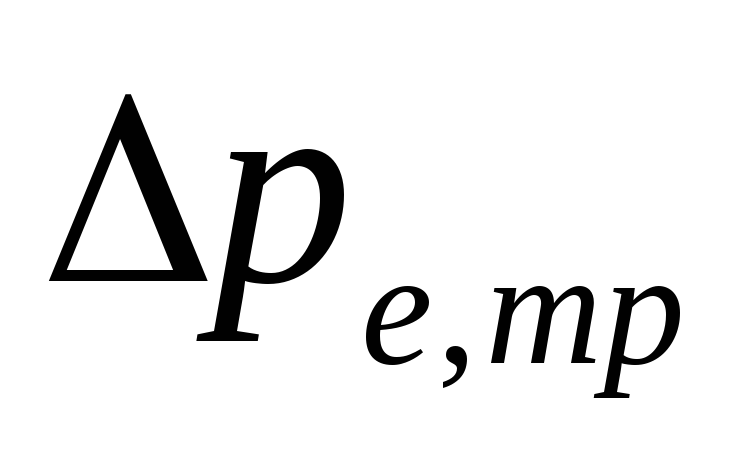
přirozený tlak dovnitř
v důsledku vodního chlazení v potrubí
.
PROTI
čerpací systémy se spodní elektroinstalací
velikost
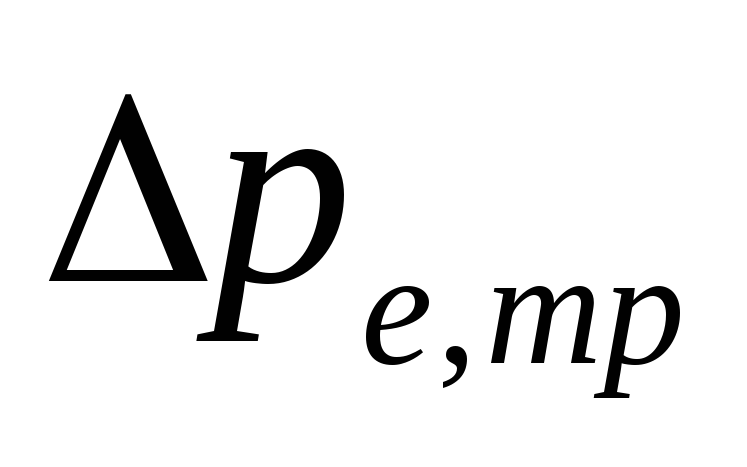
-
Jsou určeny
specifická tlaková ztráta třením
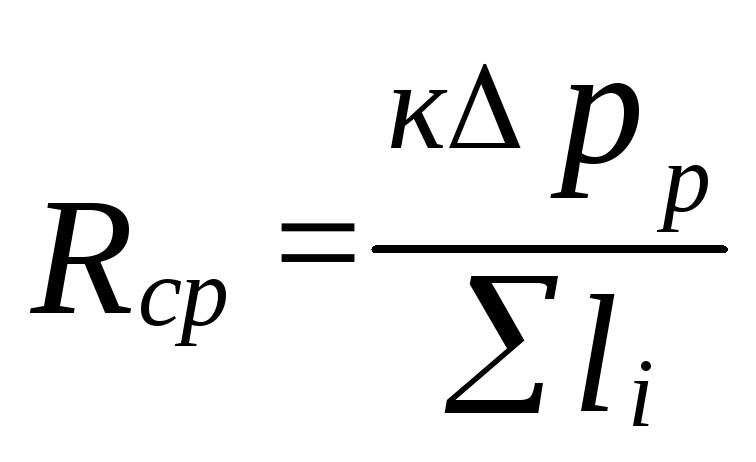
(5.4)
kde
k=0,65 určuje podíl tlakových ztrát
pro tření.
5.
Průtok vody v oblasti je určen
vzorec
 (5.5)
(5.5)
kde
Q
- tepelné zatížení na místě, W:
(tG
— tÓ)
- teplotní rozdíl chladicí kapaliny.
6.
Podle velikosti
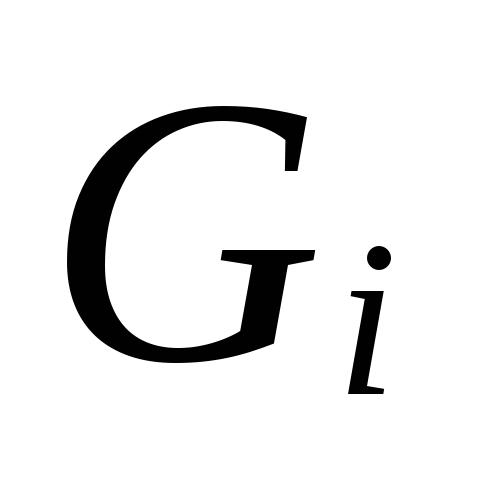
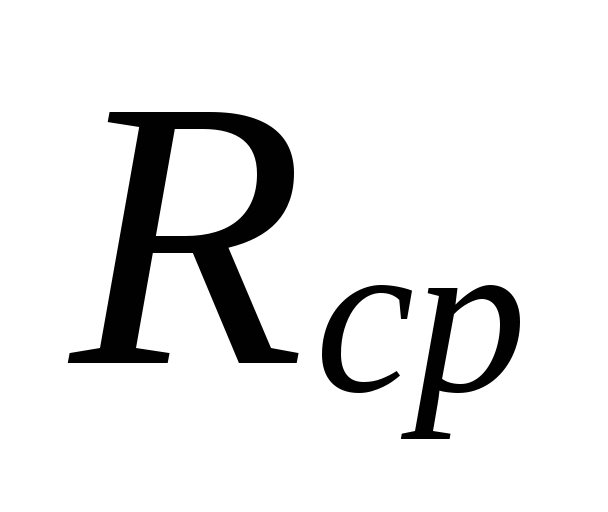
.

6.
Pro vybrané průměry potrubí
a určí se odhadovaná spotřeba vody
rychlost chladicí kapaliny proti
a skutečné konkrétní
ztráta třecího tlaku RF.
Na
výběr průměrů v oblastech s malými
průtoky chladicí kapaliny mohou být
velké rozpory mezi
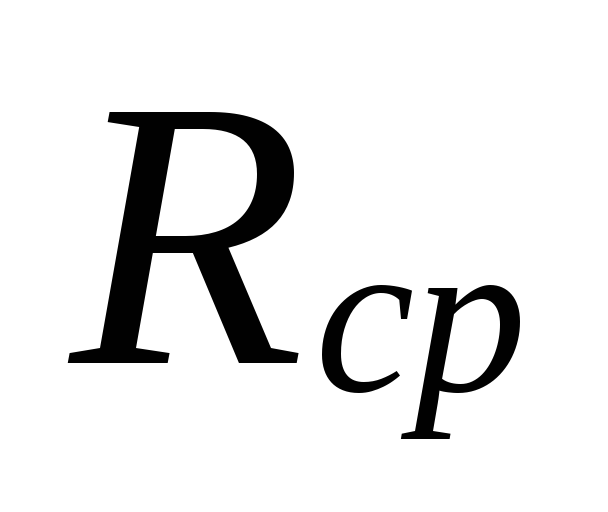
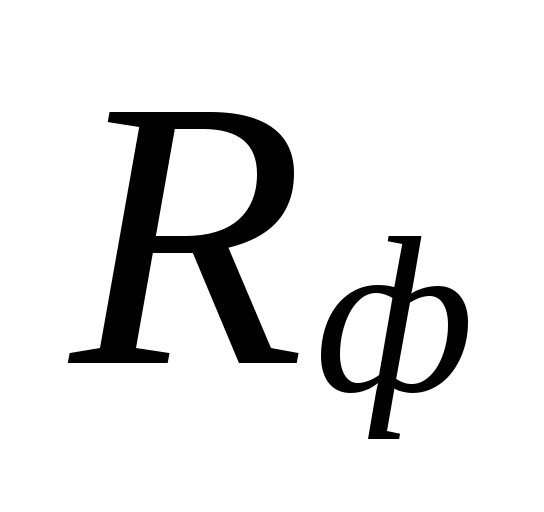
podceněné ztráty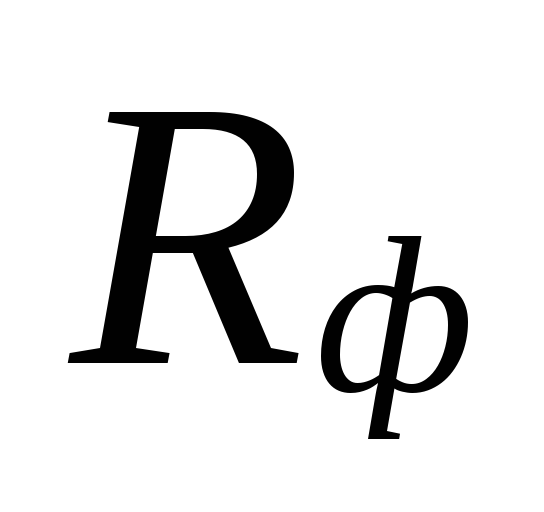
tyto oblasti jsou kompenzovány nadhodnocením
množství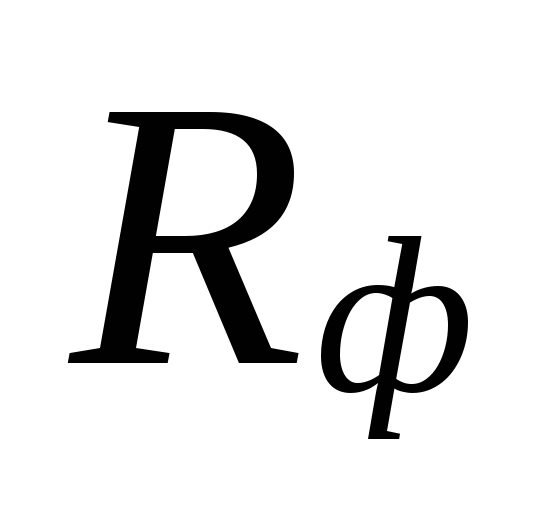
7.
Zjišťují se tlakové ztráty třením
na vypočtené ploše, Pa:
 .
.
(5.6)
Výsledek
výpočty jsou uvedeny v tabulce 5.2.
8.
Tlakové ztráty v místním
odpory pomocí buď vzorce:
 ,
,
(5.7)
kde
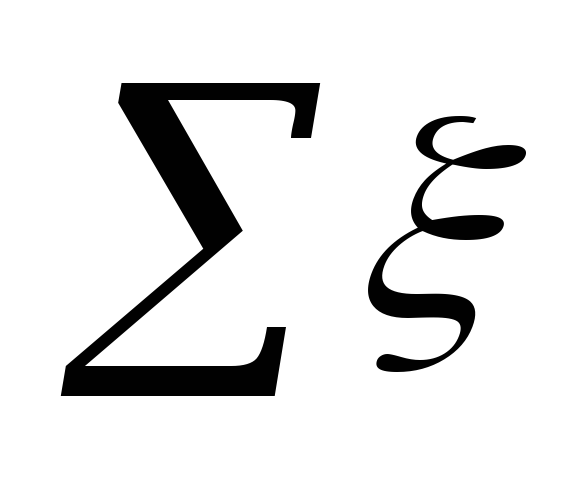
v oblasti osídlení.
Význam ξ
na každém místě jsou shrnuty v tabulce. 5.3.
Tabulka 5.3 -
Lokální koeficienty odporu
|
č. p / p |
Jména |
Hodnoty |
Poznámky |
9.
Určete celkovou tlakovou ztrátu
v každé oblasti
 .
.
(5.8)
10. Určit
celková tlaková ztráta v důsledku tření a
v místních odporech v hlavní
oběhový kroužek
 .
.
(5.9)
11. Porovnejte Δp
S ΔpR.
Celková tlaková ztráta v prstenci
musí být menší než ΔpR
na
 .
.
(5.10)
zásoby na jedno použití
tlak je potřeba na nezdůvodněný v
výpočet hydraulického odporu.
Pokud nejsou podmínky
se provádějí, je třeba na některých
části prstence pro změnu průměrů trubek.
12. Po výpočtu
hlavní oběhový kroužek
proveďte spojení zbývajících kroužků. PROTI
každý nový kroužek se počítá pouze
další neobvyklé oblasti,
zapojeny paralelně se sekcemi
hlavní kroužek.
Nesoulad ztráty
tlaky na paralelně připojené
pozemky povoleny do 15 % se slepou uličkou
pohyb vody a až 5% - s průchodem.
stůl
5.2 - Výsledky hydraulického výpočtu
pro topný systém
|
Na |
Podle |
Podle |
||||||||||||||
|
Číslo |
tepelný |
Spotřeba |
Délka |
Průměr |
Rychlost |
Charakteristický |
Ztráty |
Součet |
Ztráty |
d, |
proti, |
R, |
Δptr, |
∑ξ |
Z, |
Rl+Z, |
Lekce 6
Změna teploty plynu podél délky plynovodu
Při stacionárním proudění plynu hmotnost
průtok v plynovodu je
 . (2.41)
. (2.41)
Ve skutečnosti pohyb plynu v plynovodu
je vždy neizotermní. PROTI
Při kompresi se plyn zahřívá.
I po jeho ochlazení na COP se teplota
plyn vstupující do potrubí
je asi 2040С,
která je mnohem vyšší než teplota
prostředí (T).
V praxi se teplota plynu stává
blízko okolní teplotě
pouze pro plynovody malého průměru
(Dy0.
Navíc je třeba vzít v úvahu, že
potrubím plyn
je skutečný plyn, který je vlastní
Joule-Thompsonův efekt, který bere v úvahu
absorpce tepla při expanzi plynu.
Když se teplota po délce mění
je popsán pohyb plynu v plynovodu
soustava rovnic:
specifická energie ,
,
kontinuita ,
,
státy ,
,
tepelná bilance .
.
Uvažujme v první aproximaci rovnici
tepelnou bilanci bez zohlednění vlivu
Joule Thompson. Integrace rovnice
tepelná bilance
 ,
,
dostaneme
 , (2.42)
, (2.42)
kde ;
;
KSR- průměr na webu plný
součinitel prostupu tepla z plynu do
životní prostředí;
G je hmotnostní průtok plynu;
CP–
průměrná izobarická tepelná kapacita plynu.
hodnotatL se nazývá bezrozměrné kritérium
Šuchov
 (2.43)
(2.43)
Takže teplota plynu na konci
plynovod bude
 . (2.44)
. (2.44)
Ve vzdálenosti x od začátku
určuje se teplota plynu v plynovodu
podle vzorce
 . (2.45)
. (2.45)
Změna teploty podél délky plynovodu
je exponenciální (obr.
2.6).
Zvážit
vliv změny teploty plynu na
výkon potrubí.
Vynásobení obou stran konkrétní rovnice
energie na 2 a vyjadř ,
,
dostaneme
 . (2.46)
. (2.46)
Hustotu plynu vyjádříme na levé straně
výrazy (2.46) ze stavové rovnice
 ,
,
součinwz rovnice kontinuity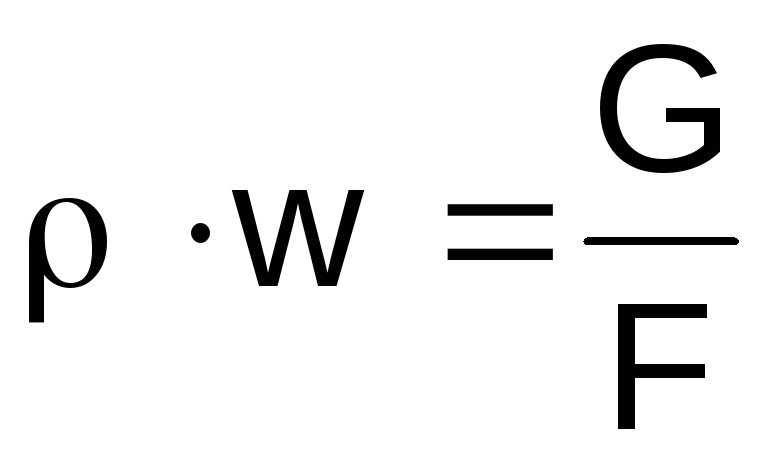
Zůstatek .
.
S ohledem na to, konkrétní rovnice
energie má formu
 (2.47)
(2.47)
nebo
 . (2.48)
. (2.48)
Označující
 a integrace levé strany rovnice
a integrace levé strany rovnice
(2,48) od PHdoPNAa vpravo od THtečkaNA, dostaneme
 . (2.49)
. (2.49)
Nahrazením
 , (2.50)
, (2.50)
my máme
 . (2.51)
. (2.51)
Po integraci ve specifik
limity, dostáváme

 . (2.52)
. (2.52)
S ohledem na (2.42)

nebo
 , (2.53)
, (2.53)
kde je korekční faktor, který bere v úvahu
je korekční faktor, který bere v úvahu
změna teploty po délce plynovodu
(neizotermie proudu plynu).
Vezmeme-li v úvahu (2.53), závislost pro urč
hmotnostní průtok plynu bude mít tvar
 . (2.54)
. (2.54)
Hodnota Hvždy větší než jedna, takže
hmotnostní průtok plynu při změně
teplota po celé délce plynovodu
(neizotermický režim proudění) vždy
méně než v izotermickém režimu
(T = tamtéž). Produkt THse nazývá střední integrál
teplota plynu v potrubí.
S hodnotami Shukhovova čísla Shu4
průtok plynu v potrubí
považovat za téměř izotermické
v T=tamtéž. Taková teplota
režim je možný při čerpání plynu s
nízké náklady na plynovod
malý (méně než 500 mm) průměr na významný
vzdálenost.
Vliv změny teploty plynu
se projevuje pro hodnoty Shukhovova čísla
Shu
Na
čerpání plynu přítomnost škrticí klapky
účinek vede k hlubšímu
chlazení plynu než pouze s výměnou tepla
s půdou. V tomto případě teplota
plyn může dokonce klesnout níže
teplota T (obr.
2.7).
Rýže. 2.7. Vliv Joule-Thompsonova jevu
na rozložení teploty plynu přes
délka potrubí
1 - bez zohlednění Di; 2 - s
s přihlédnutím k Di
Potom s přihlédnutím k Joule-Thompsonovu koeficientu
zákon změny teploty podél délky
má formu
 , (2.55)
, (2.55)
5 Hydraulické ztráty
Rozdíl
tlak oleje ve dvou částech jedné
a stejným potrubím, za předpokladu, že
první se nachází proti proudu a
druhý - níže, je určen rovnice
Bernoulli
 ,
,
kde
h2
– h1
- rozdíl výšek těžišť
sekce z libovolně zvoleného
vodorovná úroveň;
proti1,
proti2
– průměrné rychlosti oleje v úsecích;
g - zrychlení síly
gravitace;

hydraulické ztráty při pohybu
oleje z první sekce do druhé.
Rovnice
Bernoulli v plném nasazení
pro výpočet sacích potrubí čerpadel;
v ostatních případech první termín,
obvykle opomíjené a zvažované:

hydraulické
ztráty se obvykle dělí na místní
ztráty a ztráty třením po délce
potrubí (lineární).
1.5.1
lokální ztráty
energie jsou způsobeny místními
hydraulický odpor,
způsobující zkreslení proudění. Místní
odpory jsou: zúžení,
expanze, zaoblení potrubí,
filtry, ovládací zařízení a
regulace atd. Při proudění
kapaliny prostřednictvím místních odporů
jeho rychlost se mění a obvykle existují
velké víry.
Ztráty
tlak z místních odporů
určeno vzorcem Weisbach:
 MPa
MPa
(nebo
 pá),
pá),
kde

ztráta,
proti
je průměrná rychlost proudění přes průřez
v potrubí za místním odporem, m/s;
,
N/m3;
g = 9,81 m/s2.
Každý
je charakterizována lokální rezistence
hodnotou jeho koeficientu

Při turbulentním proudění jsou hodnoty
odpor a mění se velmi málo
se změnou velikosti úseku, rychlosti
průtok kapaliny a viskozita. Tak
předpokládat, že nezávisí na počtu
Reynolds Re.
Hodnoty

například pro odpaliště se stejným
průměry kanálů se berou stejně,
li:
proudy
sčítat, rozcházet; tok
míjení;









na
ohyb trubky

Hodnoty

v hydraulických systémech zařízení, převzato z
referenční literatura.
Na
laminární proudění (Re
Ztráty
tlak z místních odporů at
laminární proudění jsou určeny
vzorec:
 MPa
MPa
kde

= a

Množství
tlaková ztráta ve standardu
hydraulická zařízení pro
jmenovitý průtok obvykle
jsou uvedeny v jejich technických specifikacích.
1.5.2
Ztráta na
délkové tření
je ztráta energie, ke které dochází
v rovných trubkách konstantního průřezu,
ty. s rovnoměrným průtokem tekutiny,
a zvětšují se úměrně k délce
potrubí. Tyto ztráty jsou způsobeny vnitřními
tření v kapalině, a proto mají
umístěte do hrubých i hladkých trubek.
Ztráty
třecí tlak potrubí
je určeno vzorcem Darcy:
 MPa
MPa
kde

l
a d
- délka a vnitřní průměr potrubí,
mm.
Tento
vzorec je použitelný jak pro laminární,
stejně jako v turbulentním proudění; rozdíl
spočívá pouze v hodnotách koeficientu

Na
laminární proudění (Re
Na
turbulentní průtokový koeficient tření
není pouze funkcí Re, ale
také záleží na hrubosti vnitřního
povrch trubky. Pro hydraulicky
hladký trubky,
ty. s hrubostí, že
prakticky neovlivňuje jeho odolnost,
koeficient turbulentního tření
režim lze určit podle vzorce PC.
Konáková:

trubka
je považován za hydraulicky hladký, pokud
(d/k)>(Re/20),
kde k je ekvivalentní drsnost,
mm. Například pro novou bezešvou ocel
trubky k≈0,03
mm a po několika letech provozu
k≈0,2
mm, pro nové bezešvé trubky z
neželezné kovy k≈0,005
mm. Tyto trubky se často používají v
hydraulické systémy obráběcích strojů.
Součinitel
tření v turbulentním režimu může být
určit podle vzorce Altshulya,
být univerzální (tj. aplikovatelný
v každém případě):

2. Průtoková charakteristika modulu průtoku potrubí
Připomeňme si
lineární ztrátový vzorec - Darcyho vzorec
- Weisbach:
 .
.
Vyjádřit
v tomto vzorci rychlost V
přes tok Q
z poměru
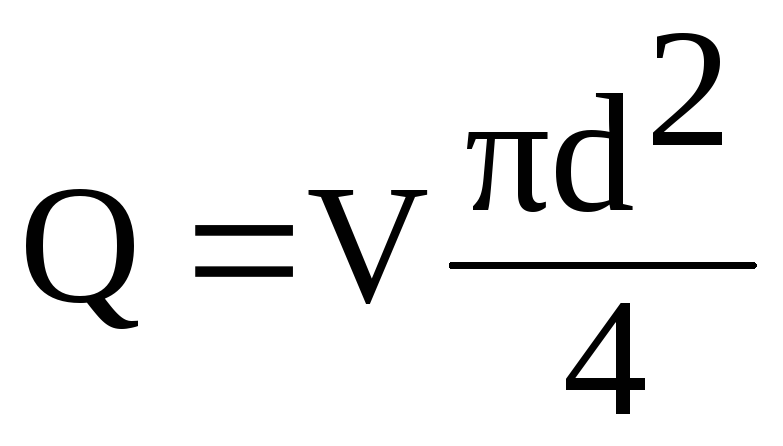
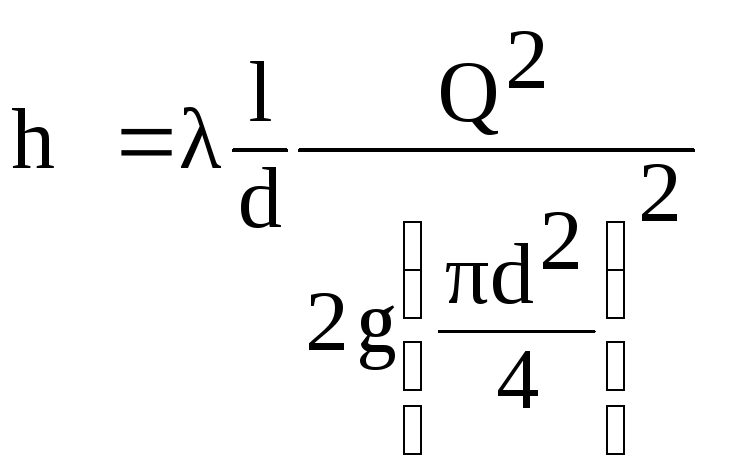
(6.1)
Pro
potrubí určitého průměru
komplexu veličin
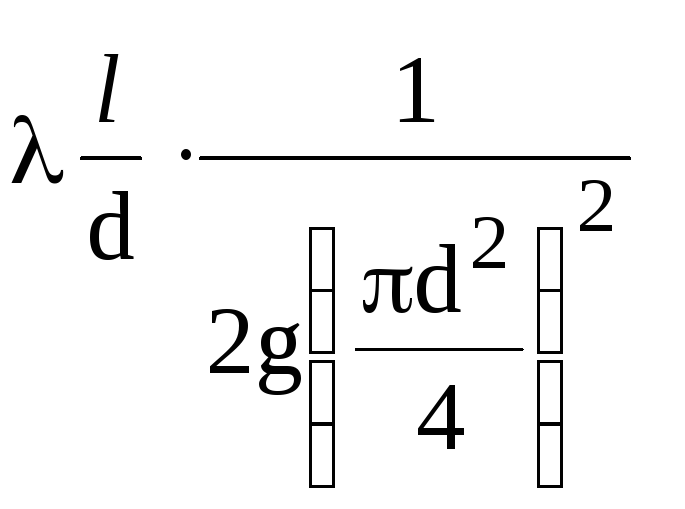
konstanta (1/K2),
kromě hydraulického koeficientu
tření λ. Na základě konceptu
průměrná ekonomická rychlost Vnapř
ukažme, že uvedený koeficient λ
lze přičíst tomuto komplexu, protože proti
V tomto případě bude Reynoldsovo číslo
mají konkrétní význam:
 ,
,
a na Nikuradzeho grafu koeficient λ in
tento případ bude mít konkrétní
význam.
Zdůvodněte
legitimitu zavedení konceptu
průměrná ekonomická rychlost následovně
uvažování.
hydraulické
systém, jako je vodovodní potrubí,
můžete přeskočit určitý výdaj
vyrobené z trubek různých průměrů. Na
Současně se zvětšením průměru d,
tedy pokles rychlosti V
porostou kapitálové výdaje a
provozní náklady budou
pokles v důsledku poklesu hydr
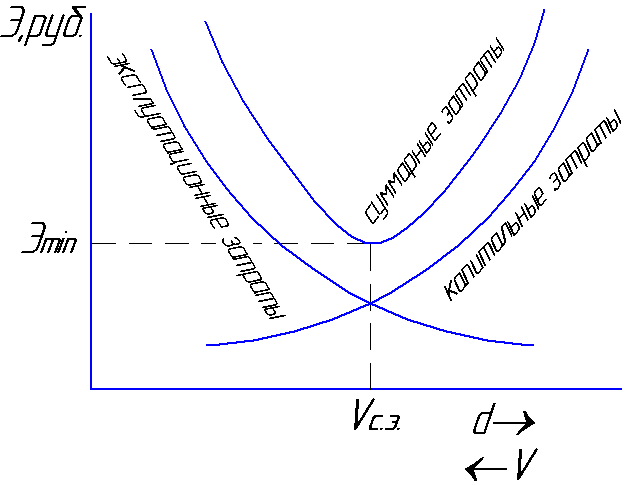
ztráty. Rychlost, jakou celkem
náklady budou minimální
bude nazýván průměrným ekonomickým
rychlost Vnapř
= 0,8 ... 1,3 m / s (obr. 6.1).
obr.6.1
Pak
lineární ztrátový vzorec (6.1) má tvar
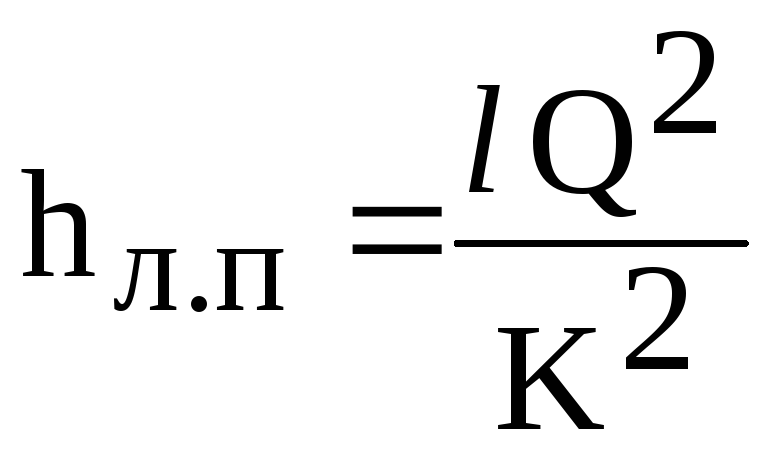
(6.2)
kde
K - průtoková charakteristika potrubí
(modul toku), v závislosti na materiálu
potrubí, průměr a průtok. je vzat
ze stolů.
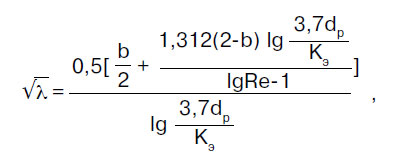
 ),C
),C ,
,