barometrický vzorec. Boltzmannovo rozdělení.
Na
odvození základní rovnice
molekulární kinetická teorie plynů
a Maxwellova distribuce molekul
rychlost se předpokládala
že vnější síly na molekuly nepůsobí
plyn, takže molekuly jsou jednotné
distribuováno podle objemu. Ale molekuly
jakéhokoli plynu jsou v potenciálu
gravitační pole Země. Společnost Gravity, s
jednu stranu a tepelný pohyb
molekuly na druhé straně vedou plyn k
nějaký ustálený stav
při kterém je tlak plynu s výškou
klesá.
Pojďme odvodit
zákon změny tlaku s výškou,
za předpokladu, že hmotnost všech
molekul je totéž, gravitační pole
homogenní a teplota je konstantní.
Obr. 1
Li
atmosférický tlak ve výšce h je
p (obr. 1), pak ve výšce h + dh se rovná p + dp
(pro dh>0 dp2:
kde
ρ je hustota plynu ve výšce h (dh je tak
málo, že při změně výšky v tomto
intervalu lze uvažovat o hustotě plynu
konstantní). Prostředek,
(1)
Vědět
stavová rovnice ideálního plynu
pV=(m/M) RT (m je hmotnost plynu, M je molární hmotnost
plyn), zjistíme, že
Střídání
je výraz v (1), dostaneme
nebo
S
změna výšky z h1 před
h2 tlak
změny od r1 před
R2 (rýže.
67), tzn.
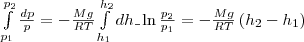
nebo
(2)
Výraz
(2) tzvbarometrický
vzorec.
Umožňuje vám vypočítat atmosféru
tlak v závislosti na nadmořské výšce popř.
měření tlaku, zjištění výšky: Od
výšky jsou uvažovány vzhledem k úrovni
moře, kde je tlak považován za normální,
pak může být reprezentován výraz (2).
tak jako
(3)
kde
p je tlak ve výšce h.
přístroj
k určení výšky nad zemí
povrch se nazývávýškoměr (nebovýškoměr).
Jeho práce je založena na aplikaci
vzorce (3). Z tohoto vzorce vyplývá, že
čím těžší plyn, tím vyšší tlak
klesá tím rychleji.
barometrický
vzorec (3) lze transformovat, jestliže
použijte vzorec p=nkT:
kde
n je koncentrace molekul ve výšce h,
n-
totéž, ve výšce h=0. Protože M=mNA (NA –
Avogadrova konstanta, m -
hmotnost jedné molekuly), a R=kNA,
pak
(4)
kde
mgh=P
je potenciální energie molekuly v
gravitační pole, tzn.
(5)
Výraz
(5) tzvrozdělení
Boltzmann pro
vnější potenciální pole. Z něj
Je vidět, že při konstantní teplotě
hustota plynu je větší tam, kde je menší
potenciální energie jeho molekul.
Li
částice jsou ve stavu chaosu
tepelný pohyb a mají stejné
hmotnost a poté Boltzmannovo rozdělení
(5) použitelný na jakýkoli vnější potenciál
pole, a to nejen v oblasti gravitace.
Jak se určuje účinnost plynové turbíny?
Zde je několik jednoduchých vzorců, které ukazují, jaká je účinnost elektrárny s plynovou turbínou:
Vnitřní výkon turbíny:
Nt = Gex * Lt, kde Lt je provoz turbíny, Gex je průtok výfukových plynů;
Vnitřní napájení GTU:
Ni gtu \u003d Nt - Nk, kde Nk je vnitřní výkon vzduchového kompresoru;
Efektivní výkon GTU:
Nef \u003d Ni gtu * Mech účinnosti, mech účinnosti - účinnost spojená s mechanickými ztrátami v ložiskách, lze vzít 0,99
Elektrická energie:
Nel \u003d Ne * účinnost např., kde účinnost např. je účinnost spojená se ztrátami v elektrickém generátoru, můžeme vzít 0,985
Dostupné teplo paliva:
Qsp = Gtop * Qrn, kde Gref - spotřeba paliva, Qrn - nejnižší pracovní výhřevnost paliva
Absolutní elektrická účinnost zařízení s plynovou turbínou:
Účinnost \u003d Nel / Q dist
kombinovaný cyklus CHP
Účinnost CCGT je vyšší než u GTU, protože zařízení s kombinovaným cyklem využívá teplo z výfukových plynů GTU. Za plynovou turbínou je instalován kotel na odpadní teplo, ve kterém je teplo z výfukových plynů plynové turbíny předáváno pracovní kapalině (napájecí vodě), vzniklá pára je posílána do parní turbíny k výrobě elektřiny a tepla.
Účinnost CCGT je obvykle reprezentována poměrem:
Účinnost PGU \u003d účinnost GTU * B + (1-GTU účinnost * B) * účinnost PSU
B je stupeň binarity cyklu
Efficiency PSU - Efektivita parní elektrárny
B = Qks/(Qks+Qku)
Qks je teplo paliva spáleného ve spalovací komoře plynové turbíny
Qku - teplo přídavného paliva spalovaného v kotli na odpadní teplo
Současně je třeba poznamenat, že pokud Qku = 0, pak B = 1, tj. instalace je zcela binární.
Vliv stupně binarity na účinnost CCGT
| B | GTU účinnost | Účinnost PSU | Účinnost CCGT |
| 1 | 0,32 | 0,3 | 0,524 |
| 1 | 0,36 | 0,32 | 0,565 |
| 1 | 0,36 | 0,36 | 0,590 |
| 1 | 0,38 | 0,38 | 0,612 |
| 0,3 | 0,32 | 0,41 | 0,47 |
| 0,4 | 0,32 | 0,41 | 0,486 |
| 0,3 | 0,36 | 0,41 | 0,474 |
| 0,4 | 0,36 | 0,41 | 0,495 |
| 0,3 | 0,36 | 0,45 | 0,51 |
| 0,4 | 0,36 | 0,45 | 0,529 |
Uveďme postupně tabulky s charakteristikami účinnosti plynových turbín a za nimi ukazatele CCGT s těmito plynovými motory a porovnejme účinnost samostatné plynové turbíny a účinnost CCGT.