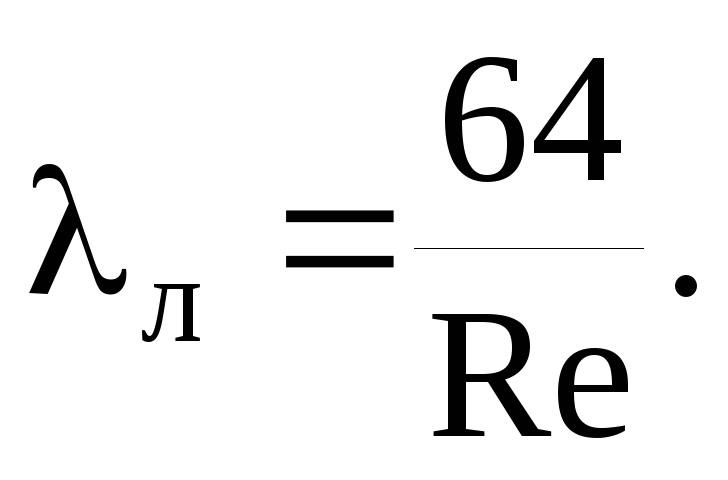1. Hydrostatisk tryk
Hydrostatisk tryk er
indre trykkraft pga
ved påvirkning af ydre kræfter påført
givet punkt i væsken. Sådan et pres
i alle retninger er det samme og afhænger
på positionen af et punkt i en væske i hvile.
Dimension af hydrostatisk tryk
i MKGSS-systemet - kg / cm2 eller t / m2,
i SI-systemet - N/m2.
Grundlæggende enhedsforhold
tryk:
|
kg/cm2 |
N/m2 |
|
|
teknisk atmosfære |
1 |
98066,5 |
|
millimeter vandsøjle |
0,0001 |
9,80665 |
|
millimeter kviksølv |
0,00136 |
133,32 |
I praktiske beregninger, 1 teknisk
atmosfære \u003d 1 kg / cm2 \u003d 10 m vand. Kunst. =
735 mmHg Kunst. = 98070 N/m2.
For en inkompressibel væske altså
i balance under kraft
tyngdekraft, fuld hydrostatisk
punkttryk:
p=p+

hvor p er trykket på den frie
flydende overflade;

højde h med areal
tværsnit lig med en;
h - nedsænkningsdybde
point;

For nogle væsker er værdierne
vægtfylde, der bruges til at løse
Opgaverne er angivet i bilaget (tab.
P-3).
Værdien af overtryk over
atmosfærisk (s-en)
kaldet manometrisk, eller
overtryk:

Hvis trykket på den frie overflade
lig med atmosfærisk, derefter overskud
tryk sm=

Under-atmosfærisk tryk
mængden kaldes vakuum:
Rwack= s-en- R.
Løsningen på de fleste problemer ved dette
afsnit er relateret til brugen
den grundlæggende ligning for hydrostatik

hvor z er koordinaten eller
punktmærke.
1. Generel information om hydraulisk beregning af rørledninger
Ved beregning
rørledninger under overvejelse
stabilt, ensartet tryk
bevægelse af enhver væske
turbulent regime, i rund-cylindrisk
rør. Væske i trykrør
er under pres og
deres tværsnit er fuldstændigt
fyldt op. Bevægelsen af væske langs
rørledning opstår som følge heraf
det faktum, at presset i starten af det er større end
til sidst.
Hydraulisk
beregningen foretages for at bestemme
rørlednings diameter d
med en kendt
længde for at sikre spring
en vis strømningshastighed Q
eller etablere
ved en given diameter og længde af det nødvendige
tryk og væskeflow. Rørledninger
afhængig af længden og mønsteret af deres
lokationer er opdelt i simple
og kompleks. Til simple rørledninger
omfatter rørledninger, der ikke har
grene på langs med en konstant
samme udgift.
Rørledninger
består af rør med samme diameter
langs hele længden eller fra sektioner af rør af forskellige
diametre og længder. Sidste sag
henviser til en seriel forbindelse.
Simple rørledninger
afhængig af længden med et plot af lokale
modstande er opdelt i korte og
lang. kort
rørledninger
er
rørledninger med en tilstrækkelig kort længde,
hvor lokal modstand
udgør mere end 10 % af hydraulikken
længdetab. For eksempel inkluderer de:
sifonrør, sug
rør til vingepumper, sifoner (tryk
vandrør under vejdæmningen),
rørledninger inde i bygninger og strukturer
etc.
lang
rørledninger
hedder
rørledninger er relativt store
længder, hvor hovedtabet på langs
væsentligt flere end lokale
tab. Lokale tab er
mindre end 5
tab langs rørledningens længde, og derfor
de kan negligeres eller introduceres kl
hydrauliske beregninger stigende
koefficient lig med 1,05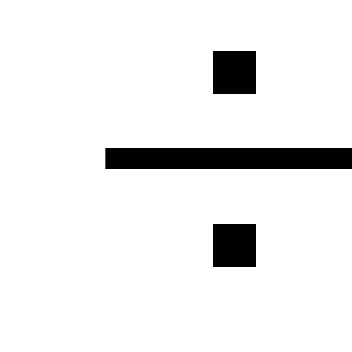
Lange rørledninger kommer ind i systemet
vandforsyningsnet, pumpeledninger
stationer, ledninger og rørledninger
industrivirksomheder og
landbrugsformål og
etc.
Komplekse rørledninger
har forskellige grene på langs,
de der. rørledningen består af et netværk af rør
visse diametre og længder. Kompleks
rørledninger er opdelt i
parallel, blindgyde (forgrenet),
ring (lukkede) rørledninger,
indgår i vandforsyningsnettet.
Hydraulisk
rørledningsberegning reduceres som
normalt for at løse tre hovedproblemer:
-
definition
rørledningsflow Q,
hvis kendt
tryk H,
længde l
og diameter d
rørledning,
givet tilgængeligheden af visse lokale
modstande eller i deres fravær; -
definition
påkrævet tryk H,
nødvendigt for at sikre et pas
kendt flow Q
ved rørledning
lang l
og diameter d; -
definition
rørlednings diameter d
hvornår
kendte hovedværdier H,
bekostning Q
og længde l.
Væskestrømningshastigheden er
hvor q > beregnet væskeflow, m3/s;
- areal af rørets spændingsførende sektion, m2.
Friktionsmodstandskoefficienten λ bestemmes i overensstemmelse med reglerne i regelsættet SP 40-102-2000 "Design og installation af rørledninger til vandforsyning og kloaksystemer lavet af polymere materialer. Generelle krav":
hvor b er et eller andet lighedsantal for væskestrømningsregimer; for b > 2 tages b = 2.
hvor Re er det faktiske Reynolds tal.
hvor ν er væskens kinematiske viskositetskoefficient, m²/s. Ved beregning af koldtvandsrør tages det lig med 1,31 10-6 m² / s - viskositeten af vand ved en temperatur på +10 ° C;
Rekv > - Reynolds tal svarende til begyndelsen af det kvadratiske område af hydraulisk modstand.
hvor Ke er rørmaterialets hydrauliske ruhed, m. For rør fremstillet af polymermaterialer tages Ke = 0,00002 m, hvis rørfabrikanten ikke opgiver andre ruhedsværdier.
I de tilfælde af flow, når Re ≥ Rekv, bliver den beregnede værdi af parameteren b lig med 2, og formel (4) forenkles betydeligt og bliver til den velkendte Prandtl-formel:
Ved Ke = 0,00002 m opstår det kvadratiske modstandsområde ved en vandstrømningshastighed (ν = 1,31 10-6 m²/s) svarende til 32,75 m/s, hvilket praktisk talt er uopnåeligt i offentlige vandforsyningssystemer.
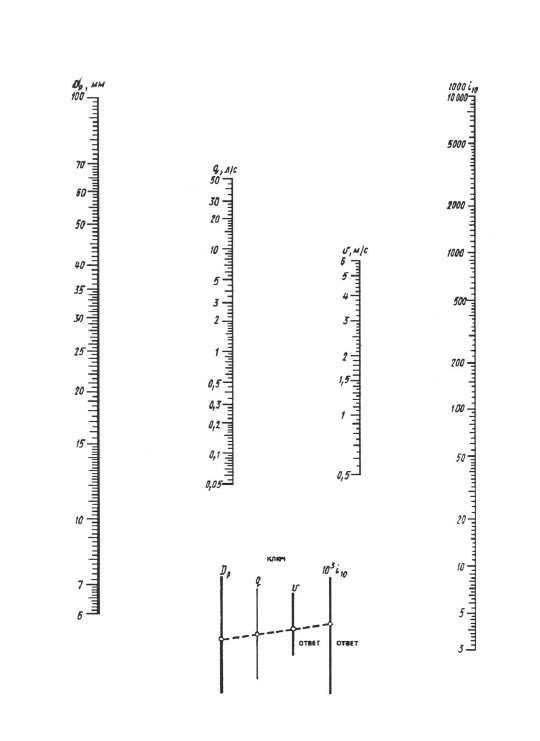
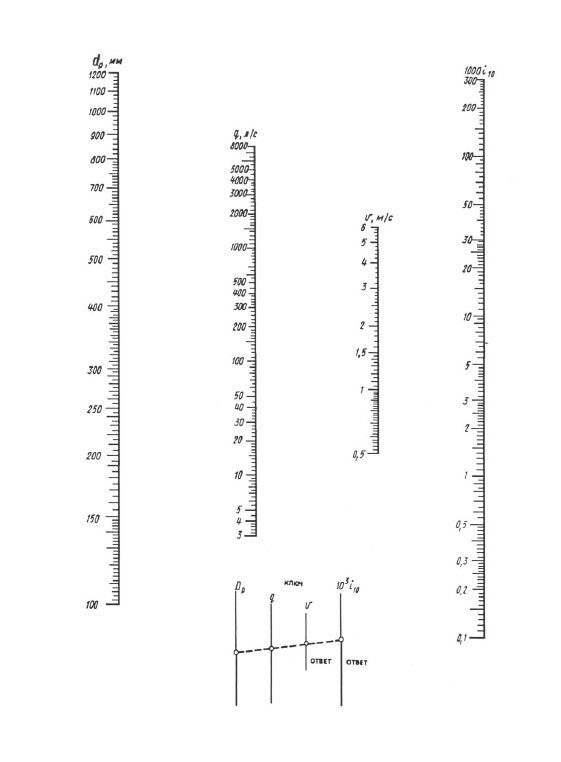
Til daglige beregninger anbefales nomogrammer, og for mere nøjagtige beregninger - "Tabeller til hydrauliske beregninger af rørledninger lavet af polymere materialer", bind 1 "Trykrørledninger" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
Ved beregning i henhold til nomogrammer opnås resultatet af en overlejring af linealen - du skal forbinde punktet med værdien af den beregnede diameter på dp-skalaen med punktet med værdien af den beregnede strømningshastighed på q (l / s) skala med en lige linje, fortsæt denne lige linje, indtil den skærer skalaerne for hastighed V og specifikke tabs hoved 1000 i (mm/m). Skæringspunkterne for en ret linje med disse skalaer giver værdien V og 1000 i.
Som du ved, er prisen på elektricitet til pumpning af væske direkte proportional med værdien af H (ceteris paribus). Hvis udtrykket ( 3 ) indsættes i formlen ( 2 ), er det let at se, at værdien af i (og følgelig H) er omvendt proportional med den beregnede diameter dp til den femte grad.
Det er vist ovenfor, at værdien af dp afhænger af tykkelsen af rørvæggen e: Jo tyndere væggen er, jo højere dp og følgelig jo lavere tryktab på grund af friktion og elektricitetsomkostninger.
Hvis rørets MRS-værdi af en eller anden grund ændres, skal dets diameter og vægtykkelse (SDR) genberegnes.
Man skal huske på, at brugen af rør med MRS 10 i stedet for rør med MRS 8, især rør med MRS 6.3, gør det muligt at reducere rørledningens diameter med én størrelse. Derfor i vores tid tillader brugen af polyethylen PE 80 (MRS 8) og PE 100 (MRS 10) i stedet for polyethylen PE 63 (MRS 6.3) til fremstilling af rør ikke kun at reducere vægtykkelsen af rør, deres vægt og materialeforbrug, men også for at reducere energiomkostningerne til pumpning af væske (ceteris paribus).
I de senere år (efter 2013) er rør lavet af PE80 polyethylen næsten fuldstændigt blevet erstattet fra produktionen af rør lavet af PE100 polyethylen. Dette forklares med, at råvarerne, som rørene er lavet af, er leveret fra udlandet med mærket PE100.Og også af det faktum, at polyethylen 100 kvalitet har flere styrkeegenskaber, på grund af hvilke rør produceres med de samme egenskaber som rør lavet af PE80, men med en tyndere væg, hvilket øger gennemstrømningen af polyethylenrørledninger.
Nomogram til bestemmelse af tryktab i rør med diametre på 6.100 mm.
Nomogram til bestemmelse af tryktab i rør med diametre på 100, 1200 mm.
Reynolds kriterium
Denne afhængighed blev frembragt af den engelske fysiker og ingeniør Osborne Reynolds (1842-1912).
Det kriterium, der hjælper med at besvare spørgsmålet om, hvorvidt der er behov for at overveje viskositet, er Reynolds-tallet Re. Det er lig med forholdet mellem bevægelsesenergien af et element af en strømmende væske og arbejdet med interne friktionskræfter.
Overvej et kubisk væskeelement med kantlængde n. Den kinetiske energi af et grundstof er:
Ifølge Newtons lov er friktionskraften, der virker på et flydende element, defineret som følger:
Denne krafts arbejde, når et flydende element flyttes over en afstand n er
og forholdet mellem fluidelementets kinetiske energi og friktionskraftens arbejde er
Vi reducerer og får:
Re kaldes Reynolds-nummeret.
Re er således en dimensionsløs størrelse, der karakteriserer den relative rolle af viskøse kræfter.
For eksempel, hvis dimensionerne af det legeme, som væsken eller gassen er i kontakt med, er meget små, så vil Re selv med en lav viskositet være ubetydelig, og friktionskræfter spiller en fremherskende rolle. Tværtimod, hvis kroppens dimensioner og hastigheden er store, så vil Re >> 1 og selv en stor viskositet næsten ikke have nogen indflydelse på bevægelsens art.
Ikke altid store Reynolds-tal betyder dog, at viskositeten ikke spiller nogen rolle. Så når en meget stor (flere titusinder eller hundredetusinder) værdi af Re-tallet nås, bliver en glat laminær (fra latin lamina - "plade") til en turbulent (fra latin turbulentus - "stormfuld" , "kaotisk"), ledsaget af kaotiske, ustabile bevægelser væsker. Denne effekt kan observeres, hvis du gradvist åbner en vandhane: en tynd strøm flyder normalt jævnt, men med en stigning i vandhastigheden forstyrres strømmens jævnhed. I en stråle, der strømmer ud under højt tryk, bevæger væskepartikler sig tilfældigt, oscillerende, al bevægelse er ledsaget af stærk blanding.
Forekomsten af turbulens øger modstanden betydeligt. I en rørledning er den turbulente strømningshastighed mindre end den laminære strømningshastighed ved samme trykfald. Men turbulens er ikke altid dårlig. På grund af det faktum, at blanding under turbulens er meget betydelig, sker varmeoverførsel - afkøling eller opvarmning af aggregater - meget mere intensivt; kemiske reaktioner spredes hurtigere.
Bernoullis ligning for stationær bevægelse
En af hydromekanikkens vigtigste ligninger blev opnået i 1738 af den schweiziske videnskabsmand Daniel Bernoulli (1700-1782). Han formåede først at beskrive bevægelsen af en ideel væske, udtrykt i Bernoulli-formlen.
En ideel væske er en væske, hvori der ikke er friktionskræfter mellem elementerne i en ideel væske, såvel som mellem den ideelle væske og karrets vægge.
Ligningen for stationær bevægelse, der bærer hans navn, er:
hvor P er væskens tryk, ρ er dens massefylde, v er bevægelseshastigheden, g er accelerationen af frit fald, h er højden, hvor væskens element er placeret.
Betydningen af Bernoulli-ligningen er, at inde i et system fyldt med væske (rørledningssektion) er den samlede energi af hvert punkt altid uændret.
Bernoulli-ligningen har tre led:
- ρ⋅v2/2 - dynamisk tryk - kinetisk energi pr. volumenenhed af drivvæsken;
- ρ⋅g⋅h - vægttryk - potentiel energi af en enhedsvolumen væske;
- P - statisk tryk, i sin oprindelse er arbejdet med trykkræfter og repræsenterer ikke en reserve af nogen speciel type energi ("trykenergi").
Denne ligning forklarer, hvorfor strømningshastigheden i snævre sektioner af røret stiger, og trykket på rørvæggene falder. Det maksimale tryk i rørene indstilles præcist på det sted, hvor røret har det største tværsnit. Smalle dele af røret er sikre i denne henseende, men trykket i dem kan falde så meget, at væsken koger, hvilket kan føre til kavitation og ødelæggelse af rørmaterialet.
Navier-Stokes ligning for viskøse væsker
I en mere stringent formulering kaldes den lineære afhængighed af viskøs friktion af ændringen i væskehastigheden Navier-Stokes-ligningen. Den tager højde for komprimerbarheden af væsker og gasser og er, i modsætning til Newtons lov, gyldig ikke kun nær overfladen af et fast legeme, men også på ethvert punkt i væsken (nær overfladen af et fast legeme i tilfælde af et inkompressibelt legeme væske, Navier-Stokes-ligningen og Newtons lov falder sammen).
Alle gasser, for hvilke betingelsen for et kontinuerligt medium er opfyldt, overholder også Navier-Stokes-ligningen, dvs. er newtonske væsker.
Viskositeten af væsker og gasser er normalt signifikant ved relativt lave hastigheder, derfor siges det nogle gange, at Euler hydrodynamik er et særligt (begrænsende) tilfælde af høje hastigheder af Navier-Stokes hydrodynamik.
Ved lave hastigheder, i overensstemmelse med Newtons lov om viskøs friktion, er kroppens modstandskraft proportional med hastigheden. Ved høje hastigheder, når viskositeten ophører med at spille en væsentlig rolle, er kroppens modstand proportional med kvadratet af hastigheden (som først blev opdaget og underbygget af Newton).
Hydraulisk beregningssekvens
1.
Hovedcirkulationen er valgt
ringvarmesystem (de fleste
ugunstigt placeret i hydraulikken
forhold). I blindgyde to-rør
systemer er en ring, der går igennem
nederste instrument af den fjerneste og
belastet stigrør, i enkeltrør -
gennem den mest fjerntliggende og indlæste
stigerør.
For eksempel,
i et to-rørs varmeanlæg med
øvre ledningshovedcirkulation
ringen vil passere fra varmepunktet
gennem hovedstigrøret, forsyningsledningen,
gennem det fjerneste stigrør, opvarmning
nedenunder apparat, returledning
til varmepunktet.
V
systemer med tilhørende vandbevægelse ind
ringen tages som den vigtigste,
passerer mest gennem midten
ladet stativ.
2.
Hovedcirkulationsringen går i stykker
i plots (plottet er karakteriseret
konstant vandstrøm og det samme
diameter). Diagrammet viser
sektionsnumre, deres længder og termiske
belastninger. Termisk belastning af hoved
plots bestemmes ved summering
termiske belastninger, der betjenes af disse
grunde. For at vælge rørdiameter
der bruges to mængder:
en)
givet vandstrøm;
b)
omtrentlige specifikke tryktab
for friktion i designcirkulationen
ring Rons.
Til
beregning Rcp
brug for at kende længden af hovedet
cirkulationsring og beregnet
cirkulationstryk.
3.
Det beregnede oplag
formeltryk
 ,
,
(5.1)
hvor
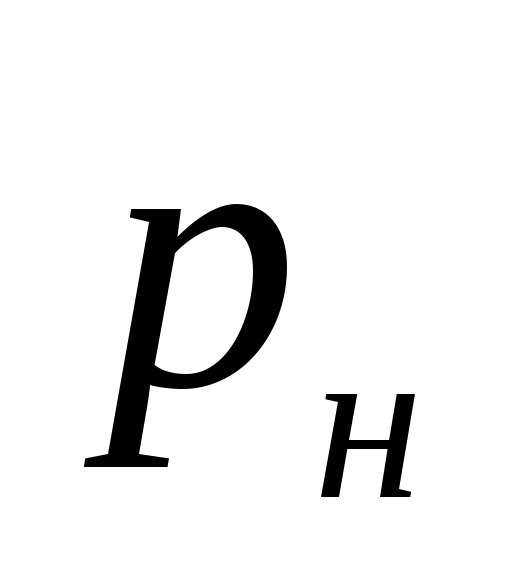
tryk skabt af pumpen, Pa.
System Design Praksis
opvarmning viste, at den mest
det er tilrådeligt at tage trykket fra pumpen,
lige
 ,
,
(5.2)
hvor
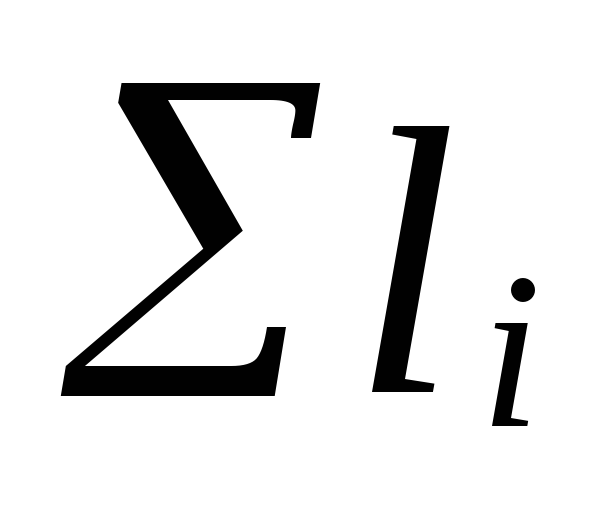
summen af længderne af hovedcirkulationens sektioner
ringe;
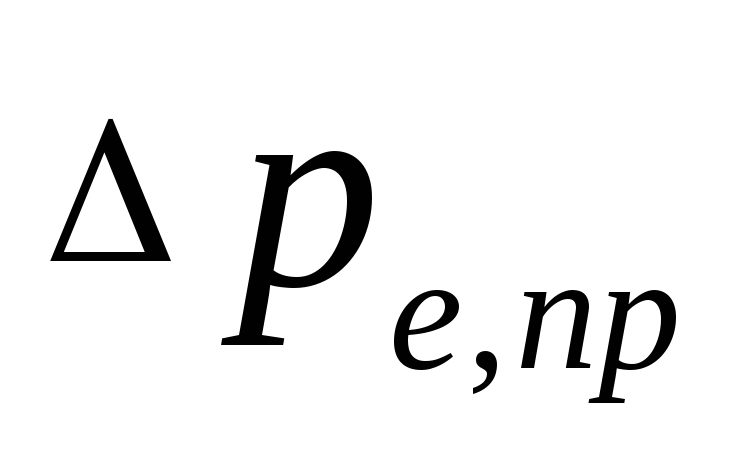
naturligt tryk, der opstår når
vandkøling i hvidevarer, Pa, evt
bestemme hvordan
 ,
,
(5.3)
hvor
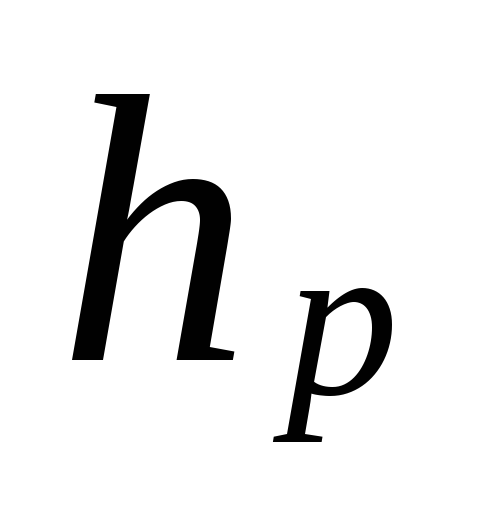
afstand fra midten af pumpen (elevator)
til midten af enheden i den nederste etage, m.
Betyder
koefficient muligt
bestemme ud fra tabel 5.1.
bord
5.1 - Betydning c
afhængig af designtemperaturen
vand i varmesystemet
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
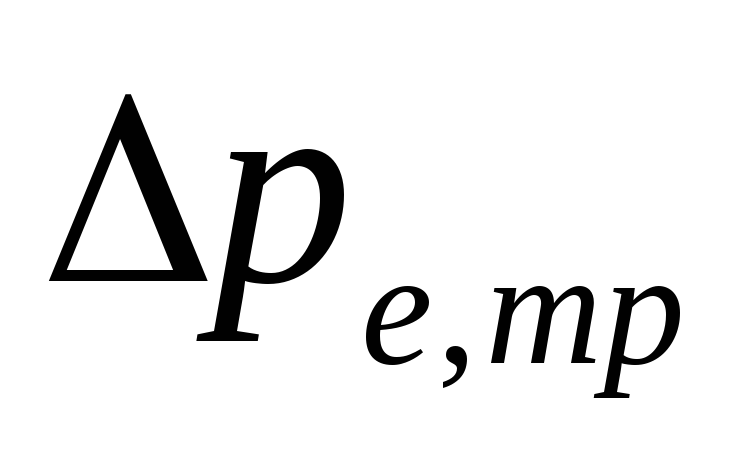
naturligt tryk ind
som følge af vandkøling i rørledninger
.
V
pumpeanlæg med bundledninger
størrelse
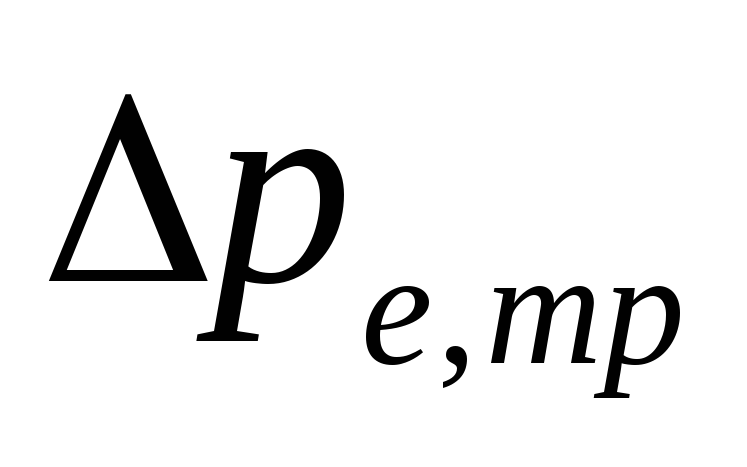
-
er bestemt
specifikt friktionstryktab
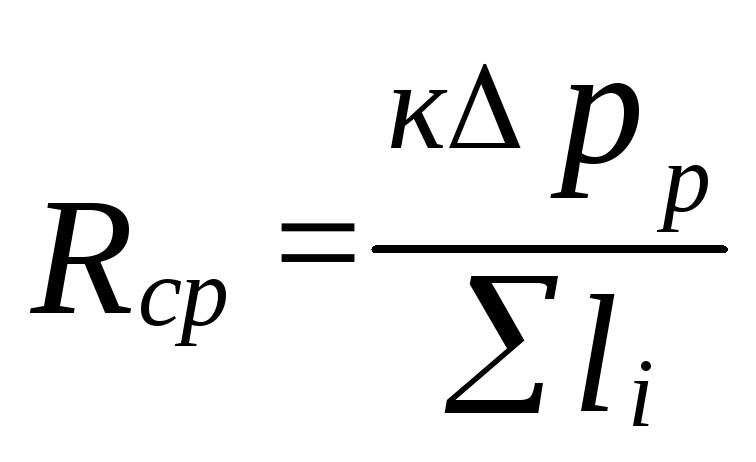
(5.4)
hvor
k=0,65 bestemmer andelen af tryktab
for friktion.
5.
Vandføringen i området er bestemt af
formel
 (5.5)
(5.5)
hvor
Q
- varmebelastning på stedet, W:
(tG
— tO)
- temperaturforskel på kølevæsken.
6.
Efter størrelsesorden
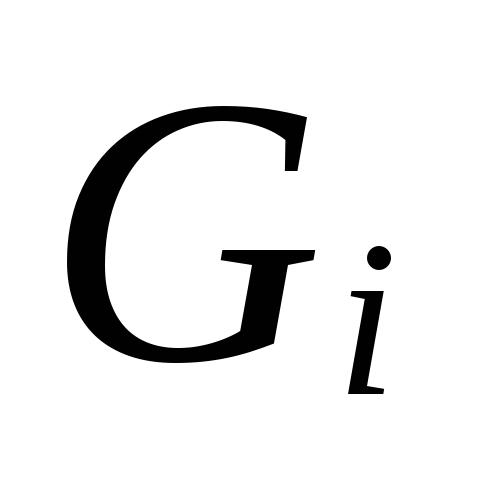
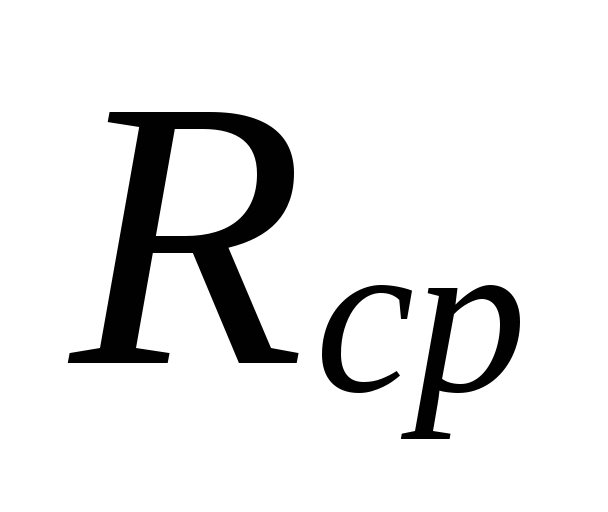
.

6.
Til udvalgte rørledningsdiametre
og estimeret vandforbrug fastlægges
kølevæskehastighed v
og den faktiske specifikke
friktionstryktab Rf.
På
valg af diametre i områder med små
kølevæskestrømningshastigheder kan være
store uoverensstemmelser imellem
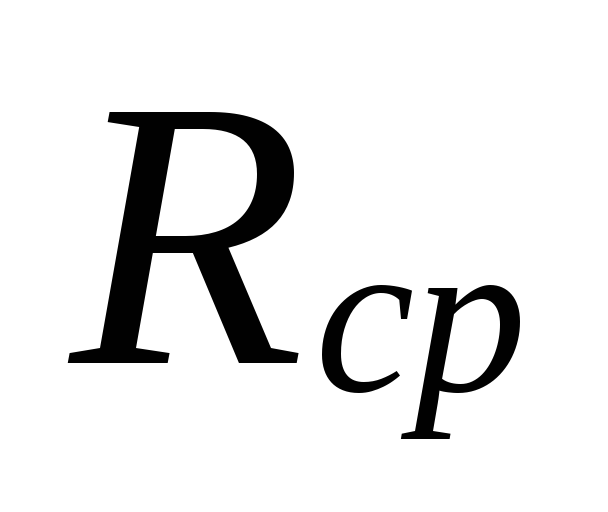
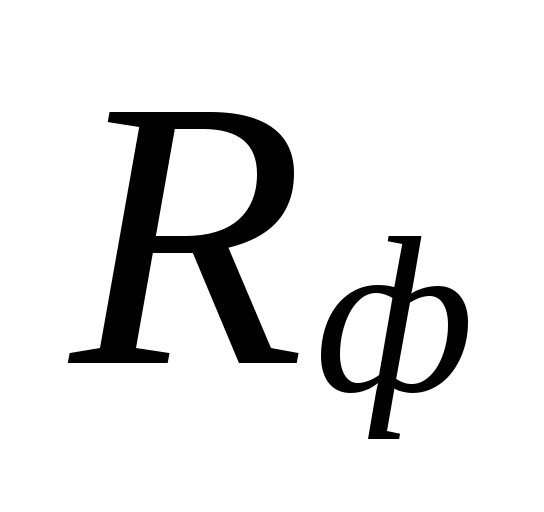
undervurderede tab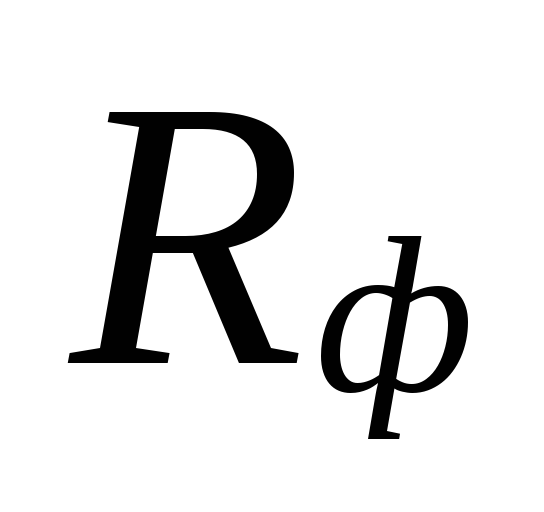
disse arealer kompenseres af en overvurdering
mængder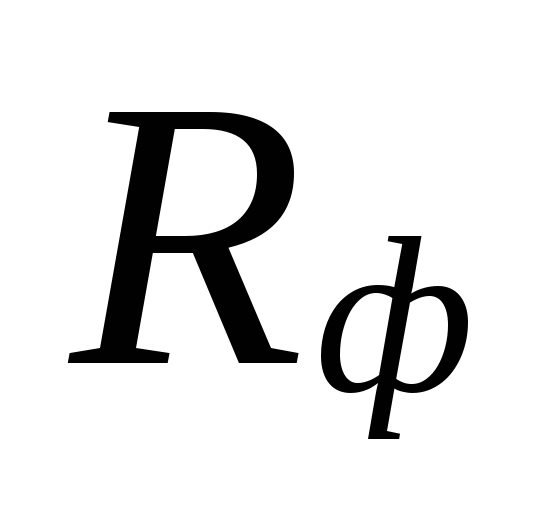
7.
Friktionstryktab bestemmes
på det beregnede areal, Pa:
 .
.
(5.6)
resultater
beregninger er indtastet i tabel 5.2.
8.
Tryktab i lokale
modstande ved hjælp af enten formlen:
 ,
,
(5.7)
hvor
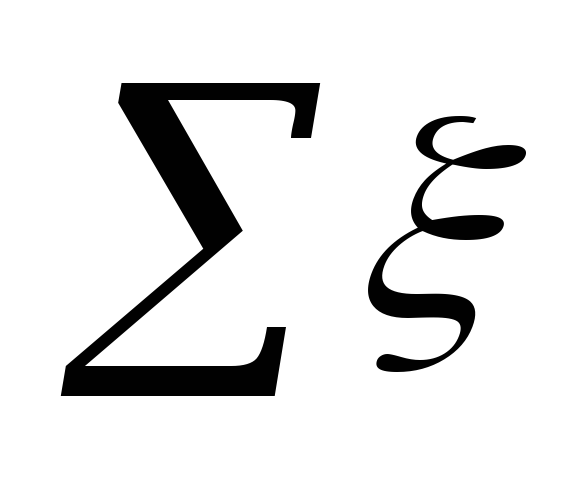
i bebyggelsesområdet.
Betyder ξ
på hvert sted er opsummeret i tabellen. 5.3.
Tabel 5.3 -
Lokale modstandskoefficienter
|
nr. p / p |
Navne |
Værdier |
Noter |
9.
Bestem det samlede tryktab
på alle områder
 .
.
(5.8)
10. Bestem
totalt tryktab på grund af friktion og
i hovedsagen lokale modstande
cirkulationsring
 .
.
(5.9)
11. Sammenlign Δp
Med ΔpR.
Totalt tryktab over ringen
skal være mindre end ΔpR
på den
 .
.
(5.10)
lager af engangs
der er behov for pres på uforudset i
beregning af hydraulisk modstand.
Hvis forholdene ikke er det
udføres, er det nødvendigt på nogle
sektioner af ringen for at ændre diameteren af rørene.
12. Efter beregning
hovedcirkulationsring
lav sammenkoblingen af de resterende ringe. V
hver ny ring tæller kun
yderligere ikke-fælles områder,
forbundet parallelt med sektioner
hovedring.
Tab uoverensstemmelse
tryk på parallelforbundet
tomter tilladt op til 15% med en blindgyde
bevægelsen af vand og op til 5% - med forbigående.
bord
5.2 - Resultater af hydraulisk beregning
til varmeanlæg
|
På den |
Ved |
Ved |
||||||||||||||
|
Nummer |
termisk |
Forbrug |
Længde |
Diameter |
Fart |
Bestemt |
Tab |
Sum |
Tab |
d, |
v, |
R, |
Δptr, |
∑ξ |
Z, |
Rl+Z, |
Lektion 6
Ændring i gastemperatur langs længden af gasrørledningen
Ved stationær gasstrøm er massen
flowhastigheden i gasrørledningen er
 . (2.41)
. (2.41)
Faktisk bevægelsen af gas i gasrørledningen
er altid ikke-isotermisk. V
Under kompression opvarmes gassen.
Selv efter afkøling ved COP, temperaturen
gas, der kommer ind i rørledningen
er omkring 2040С,
hvilket er meget højere end temperaturen
miljø (T).
I praksis bliver gassens temperatur
tæt på den omgivende temperatur
kun for gasrørledninger med lille diameter
(Dy0.
Det skal der desuden tages højde for
rørledningsgas
er en rigtig gas, som er iboende
Joule-Thompson effekten, som tager højde for
absorption af varme under gasudvidelse.
Når temperaturen ændres på langs
gasrørledningens gasbevægelse er beskrevet
ligningssystem:
specifik energi ,
,
kontinuitet ,
,
stater ,
,
varmebalance .
.
Overvej ligningen i den første tilnærmelse
varmebalance uden hensyntagen til effekten
Joule Thompson. Integrering af ligningen
varmebalance
 ,
,
vi får
 , (2.42)
, (2.42)
hvor ;
;
KSR- gennemsnit på webstedet fuld
varmeoverførselskoefficient fra gas til
miljø;
G er gassens massestrømshastighed;
cP–
Gassens gennemsnitlige isobariske varmekapacitet.
en værditL kaldes det dimensionsløse kriterium
Shukhov
 (2.43)
(2.43)
Så gastemperaturen til sidst
gasrørledning bliver
 . (2.44)
. (2.44)
På afstand x fra begyndelsen
gasrørledningens gastemperatur bestemmes
efter formlen
 . (2.45)
. (2.45)
Ændring i temperatur langs længden af gasrørledningen
er eksponentiel (fig.
2.6).
Overveje
effekt af gastemperaturændring på
pipeline ydeevne.
Multiplicer begge sider af den specifikke ligning
energi på 2 og udtrykke ,
,
vi får
 . (2.46)
. (2.46)
Vi udtrykker densiteten af gassen på venstre side
udtryk (2.46) fra tilstandsligningen
 ,
,
produktwfra kontinuitetsligningen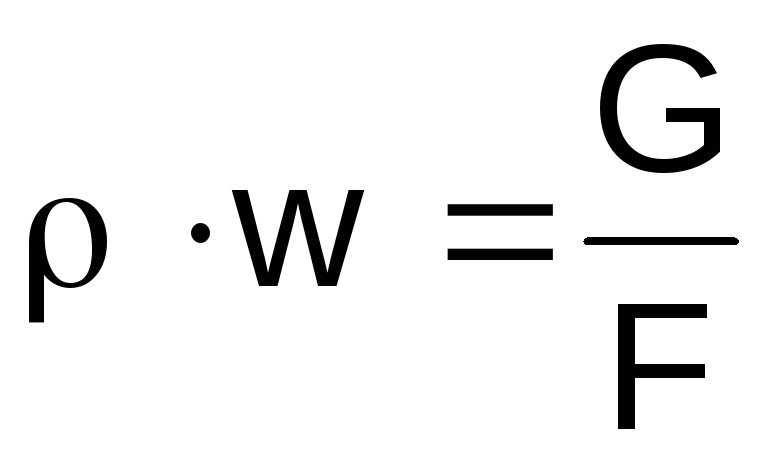
balance .
.
Med dette i tankerne, den specifikke ligning
energi tager form
 (2.47)
(2.47)
eller
 . (2.48)
. (2.48)
Betegner
 og integration af venstre side af ligningen
og integration af venstre side af ligningen
(2.48) fra PHdoPTIL, og til højre fra THdoTTIL, vi får
 . (2.49)
. (2.49)
Ved at udskifte
 , (2.50)
, (2.50)
vi har
 . (2.51)
. (2.51)
Efter integration i det angivne
grænser, får vi

 . (2.52)
. (2.52)
Under hensyntagen til (2,42)

eller
 , (2.53)
, (2.53)
hvor er en korrektionsfaktor, der tager højde for
er en korrektionsfaktor, der tager højde for
temperaturændring i længden af gasrørledningen
(ikke-isotermalitet af gasstrømmen).
Under hensyntagen til (2.53), afhængigheden for at bestemme
massestrømshastigheden af gas vil tage formen
 . (2.54)
. (2.54)
Værdi Haltid større end én, så
massestrømshastighed af gas ved skift
temperatur langs længden af gasrørledningen
(ikke-isotermisk strømningsregime) altid
mindre end i isotermisk tilstand
(T=idem). Produkt THkaldes middelintegralet
temperatur på gassen i rørledningen.
Med værdierne af Shukhov-tallet Shu4
gasstrøm i rørledningen
overveje næsten isotermisk
ved T=idem. Sådan en temperatur
tilstand er mulig ved pumpning af gas med
lave gasledningsomkostninger
lille (mindre end 500 mm) diameter til en betydelig
afstand.
Effekt af ændring af gastemperatur
manifesterer sig for værdierne af Shukhov-tallet
Shu
På
gaspumpe tilstedeværelsen af en gasspjæld
effekt fører til en dybere
gaskøling end kun med varmeveksling
med jord. I dette tilfælde temperaturen
gas kan endda falde under
temperatur T (fig.
2.7).
Ris. 2.7. Indflydelse af Joule-Thompson-effekten
på gastemperaturfordelingen over
rørledningens længde
1 - uden at tage hensyn til Di; 2 - med
under hensyntagen til Di
Derefter under hensyntagen til Joule-Thompson-koefficienten
lov om temperaturændring i længden
tager formen
 , (2.55)
, (2.55)
5 Hydrauliske tab
Forskel
olietryk i to sektioner af en
og samme rørledning, forudsat at
den første er placeret opstrøms, og
den anden - nedenfor, er bestemt ligning
Bernoulli
 ,
,
hvor
h2
– h1
- forskellen i højderne af tyngdepunkterne
sektioner fra en vilkårligt valgt
vandret niveau;
v1,
v2
– gennemsnitlige oliehastigheder i sektioner;
g - kraftacceleration
tyngdekraft;

hydrauliske tab under bevægelse
olier fra den første sektion til den anden.
Ligningen
Bernoulli i fuld brug
til beregning af sugeledninger af pumper;
i andre tilfælde den første periode,
normalt forsømt og overvejet:

hydraulisk
tab er normalt opdelt i lokale
tab og friktionstab på langs
rørledninger (lineær).
1.5.1
lokale tab
energier skyldes lokale
hydraulisk modstand,
forårsager flowforvrængning. Lokal
modstande er: forsnævringer,
udvidelse, afrunding af rørledninger,
filtre, kontroludstyr og
regulering osv. Ved strømning
væsker gennem lokale modstande
dens hastighed ændrer sig, og det er der normalt
store hvirvler.
Tab
pres fra lokale modstande
bestemt af formlen Weisbach:
 MPa
MPa
(eller
 Pa),
Pa),
hvor

tab,
v
er den gennemsnitlige strømningshastighed over tværsnittet
i et rør bag lokal modstand, m/s;
,
N/m3;
g=9,81 m/s2.
Hver
lokal modstand er karakteriseret
ved dens koefficientværdi

Med turbulent flow, værdierne
modstand og forandring meget lidt
med en ændring i størrelsen af sektionen, hastighed
væskeflow og viskositet. Så
antag, at de ikke er afhængige af antallet
Reynolds Re.
Værdier

for eksempel til tees med samme
kanaldiametre tages ens,
hvis:
vandløb
lægge sammen, afvige; flyde
bestået;









på
rørbøjning

Værdier

i hydrauliske systemer af udstyr, taget fra
referencelitteratur.
På
laminær strømning (vedr
Tab
pres fra lokale modstande kl
laminært flow bestemmes af
formel:
 MPa
MPa
hvor

= a

Mængder
tryktab i standard
hydrauliske anordninger til
normalt nominel strømningshastighed
anført i deres tekniske specifikationer.
1.5.2
Tab på
længde friktion
er det energitab, der opstår
i lige rør med konstant tværsnit,
de der. med ensartet væskestrøm,
og øges i forhold til længden
rør. Disse tab skyldes interne
friktion i en væske, og har derfor
placeres i både ru og glatte rør.
Tab
rørlednings friktionstryk
bestemmes af formlen Darcy:
 MPa
MPa
hvor

l
og d
- rørledningens længde og indvendige diameter
mm.
Det her
formlen gælder både for laminar,
såvel som i turbulent flow; forskel
består kun af koefficientens værdier

På
laminær strømning (vedr
På
turbulent flow friktionskoefficient
er ikke kun en funktion af Re, men
afhænger også af ruheden af det indre
rør overflade. Til hydraulisk
glat rør,
de der. med en ruhed, der
praktisk talt ikke påvirker dets modstand,
turbulent friktionskoefficient
tilstand kan bestemmes af formlen PC.
Konakova:

rør
betragtes som hydraulisk glat hvis
(d/k)>(Re/20),
hvor k er den ækvivalente ruhed,
mm. For eksempel til nyt sømløst stål
rør k≈0,03
mm, og efter flere års drift
k≈0,2
mm, til nye sømløse rør lavet af
ikke-jernholdige metaller k≈0,005
mm. Disse rør bruges ofte i
hydrauliske systemer af værktøjsmaskiner.
Koefficient
friktion i det turbulente regime kan være
bestemme efter formel Altshulya,
være universel (dvs. anvendelig
i hvert fald):

2. Flowkarakteristika for rørledningsflowmodulet
Lad os huske
lineær tabsformel - Darcy-formel
- Weisbach:
 .
.
Express
i denne formel er hastigheden V
gennem flow Q
fra forholdet
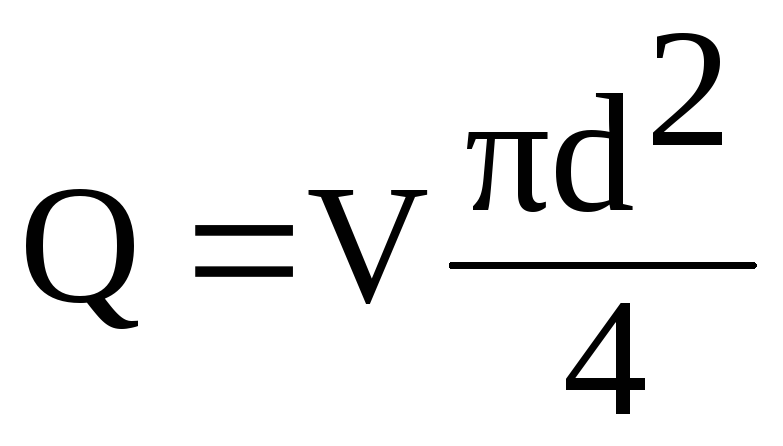
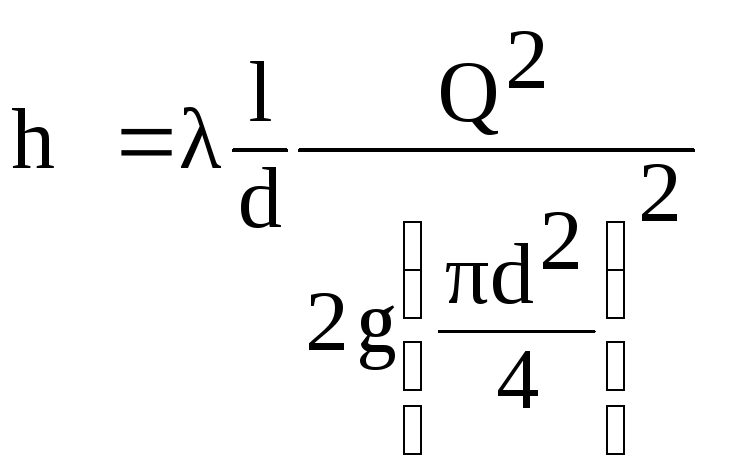
(6.1)
Til
rørledning med en vis diameter
kompleks af mængder
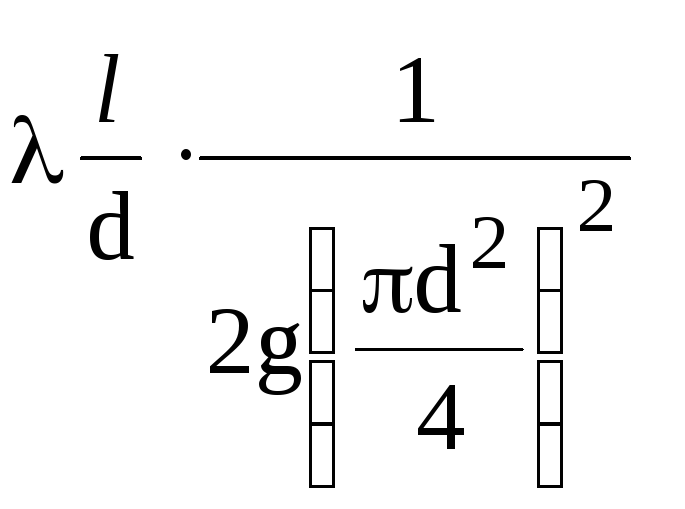
konstant (1/K2),
bortset fra den hydrauliske koefficient
friktion λ. Ud fra konceptet
gennemsnitlig økonomisk hastighed Vs.e
lad os vise, at den angivne koefficient λ
kan tilskrives dette kompleks, fordi v
I dette tilfælde vil Reynolds-nummeret være
har en bestemt betydning:
 ,
,
og på Nikuradze-plottet, koefficienten λ in
denne sag vil have en specifik
betyder.
retfærdiggøre
legitimiteten af at indføre konceptet
den gennemsnitlige økonomiske hastighed som følger
ræsonnement.
hydraulisk
system, såsom VVS,
du kan springe en bestemt udgift over
lavet af rør med forskellige diametre. På
På samme tid, med en stigning i diameteren d,
derfor et fald i hastigheden V
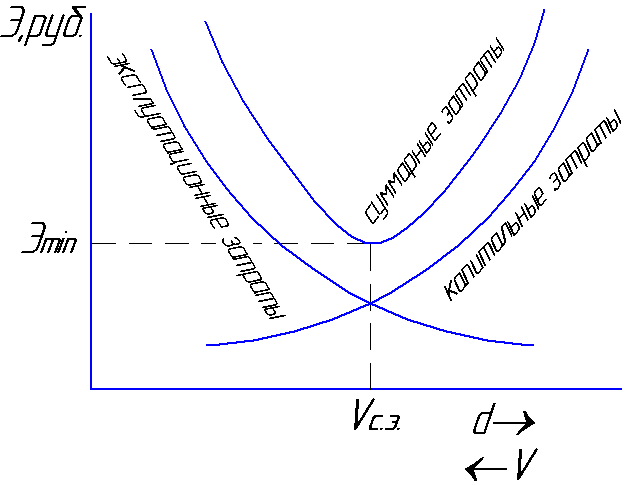
anlægsudgifter vil stige, og
driftsomkostningerne vil
fald på grund af et fald i hydraulik
tab. Den hastighed, hvormed den samlede
omkostningerne vil være minimale
vil blive kaldt den gennemsnitlige økonomiske
hastighed Vs.e
= 0,8 ... 1,3 m/s (fig. 6.1).
fig.6.1
Derefter
den lineære tabsformel (6.1) har formen
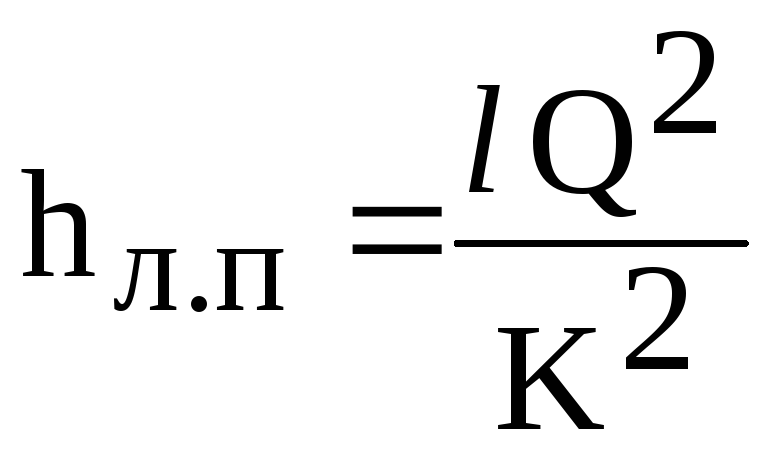
(6.2)
hvor
K - flowkarakteristisk for rørledningen
(strømningsmodul), afhængig af materiale
rørledning, diameter og flow. er taget
fra borde.
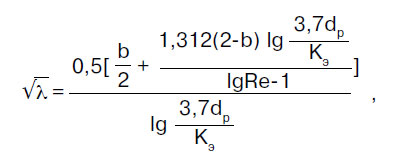
 ),C
),C ,
,