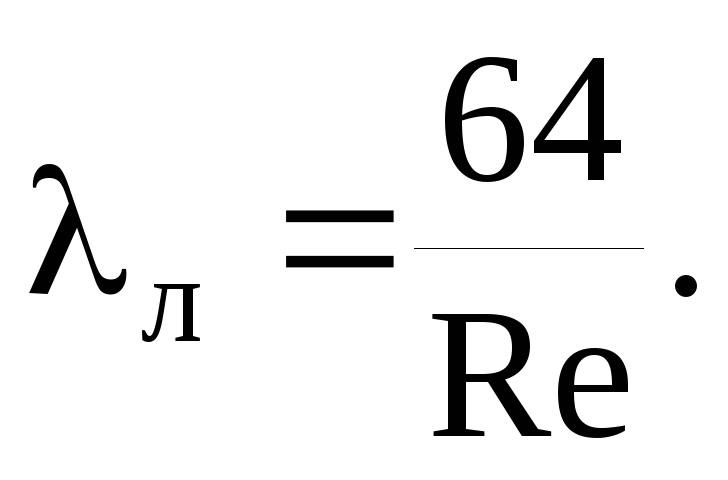1. Υδροστατική πίεση
Η υδροστατική πίεση είναι
εσωτερική θλιπτική δύναμη λόγω
από τη δράση εξωτερικών δυνάμεων που εφαρμόζονται σε
δεδομένο σημείο στο υγρό. Τέτοια πίεση
προς όλες τις κατευθύνσεις είναι το ίδιο και εξαρτάται
στη θέση ενός σημείου σε ένα υγρό σε ηρεμία.
Διάσταση υδροστατικής πίεσης
στο σύστημα MKGSS - kg / cm2 ή t / m2,
στο σύστημα SI - N/m2.
Βασικές αναλογίες μονάδων
πίεση:
|
kg/cm2 |
N/m2 |
|
|
τεχνική ατμόσφαιρα |
1 |
98066,5 |
|
χιλιοστό στήλης νερού |
0,0001 |
9,80665 |
|
χιλιοστό υδραργύρου |
0,00136 |
133,32 |
Σε πρακτικούς υπολογισμούς, 1 τεχν
ατμόσφαιρα \u003d 1 kg / cm2 \u003d 10 m νερού. Τέχνη. =
735 mmHg Τέχνη. = 98070 N/m2.
Για ένα ασυμπίεστο ρευστό δηλαδή
σε ισορροπία υπό δύναμη
βαρύτητα, πλήρης υδροστατική
σημειακή πίεση:
p=p+

όπου p είναι η πίεση στο ελεύθερο
υγρή επιφάνεια?

ύψος h με εμβαδόν
διατομή ίση με ένα.
h - βάθος βύθισης
σημεία?

Για ορισμένα υγρά, οι τιμές
ειδικό βάρος που χρησιμοποιείται στην επίλυση
οι εργασίες δίνονται στο παράρτημα (πίν.
Ρ-3).
Η τιμή της υπερπίεσης πάνω από
ατμοσφαιρική (σελένα)
που ονομάζεται μανομετρική, ή
υπερπίεση:

Εάν η πίεση στην ελεύθερη επιφάνεια
ίση με την ατμοσφαιρική, μετά την περίσσεια
πίεση σελΜ=

Υπερατμοσφαιρική πίεση
η ποσότητα ονομάζεται κενό:
Rγουκ= σελένα- Ρ.
Η λύση στα περισσότερα από τα προβλήματα αυτού
ενότητα σχετίζεται με τη χρήση
η βασική εξίσωση της υδροστατικής

όπου z είναι η συντεταγμένη ή
σημείο σημείου.
1. Γενικές πληροφορίες για τον υδραυλικό υπολογισμό αγωγών
Κατά τον υπολογισμό
αγωγών που εξετάζονται
σταθερή, ομοιόμορφη πίεση
κίνηση οποιουδήποτε υγρού
τυρβώδες καθεστώς, σε στρογγυλό-κυλινδρικό
σωλήνες. Υγρό σε σωλήνες πίεσης
βρίσκεται υπό πίεση και
οι διατομές τους είναι πλήρως
γέματο. Η κίνηση του υγρού κατά μήκος
αγωγός προκύπτει ως αποτέλεσμα
το γεγονός ότι η πίεση στην αρχή του είναι μεγαλύτερη από
στο τέλος.
Υδραυλικός
ο υπολογισμός γίνεται για να προσδιοριστεί
διάμετρος αγωγού ρε
με μια γνωστή
μήκος για να διασφαλιστεί η παράλειψη
ορισμένο ρυθμό ροής Q
ή ίδρυση
σε δεδομένη διάμετρο και μήκος του απαιτούμενου
πίεση και ροή ρευστού. Αγωγοί
ανάλογα με το μήκος και το σχέδιο τους
οι τοποθεσίες χωρίζονται σε απλές
και πολύπλοκο. Σε απλούς αγωγούς
περιλαμβάνει αγωγούς που δεν έχουν
κλαδιά κατά μήκος, με σταθερά
την ίδια δαπάνη.
Αγωγοί
αποτελείται από σωλήνες ίδιας διαμέτρου
σε όλο το μήκος ή από τμήματα σωλήνων διαφορετικών
διαμέτρους και μήκη. Τελευταία περίπτωση
αναφέρεται σε σειριακή σύνδεση.
Απλοί αγωγοί
ανάλογα με το μήκος με οικόπεδο τοπικών
οι αντιστάσεις χωρίζονται σε βραχείες και
μακρύς. μικρός
αγωγών
είναι
αγωγούς με αρκετά μικρό μήκος,
στην οποία η τοπική αντίσταση
αποτελούν περισσότερο από το 10% του υδραυλικού
απώλεια μήκους. Για παράδειγμα, περιλαμβάνουν:
σωλήνες σιφονιού, αναρρόφηση
σωλήνες αντλιών πτερυγίων, σιφώνια (πίεση
σωλήνες νερού κάτω από το ανάχωμα του δρόμου),
σωληνώσεις μέσα σε κτίρια και κατασκευές
και τα λοιπά.
Μακρύς
αγωγών
που ονομάζεται
οι αγωγοί είναι σχετικά μεγάλοι
μήκη στα οποία η απώλεια κεφαλής κατά μήκος
υπερτερούν σημαντικά σε αριθμό τοπικών
απώλειες. Τοπικές απώλειες είναι
λιγότερο από 5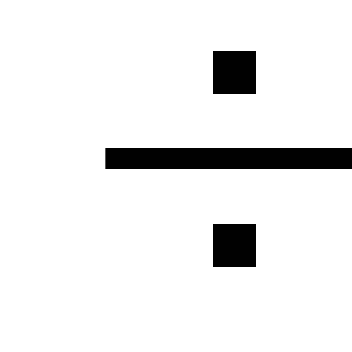
απώλειες σε όλο το μήκος του αγωγού και επομένως
μπορούν να παραμεληθούν ή να εισαχθούν στο
αυξάνονται οι υδραυλικοί υπολογισμοί
συντελεστής ίσος με 1,05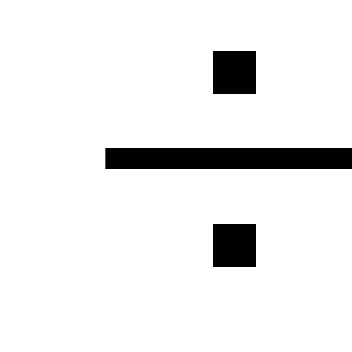
Οι μεγάλοι αγωγοί εισέρχονται στο σύστημα
δίκτυα ύδρευσης, αγωγοί άντλησης
σταθμούς, αγωγούς και αγωγούς
βιομηχανικές επιχειρήσεις και
γεωργικός σκοπός και
και τα λοιπά.
Σύνθετοι αγωγοί
έχουν διαφορετικά κλαδιά κατά μήκος,
εκείνοι. ο αγωγός αποτελείται από ένα δίκτυο σωλήνων
ορισμένες διαμέτρους και μήκη. Συγκρότημα
οι αγωγοί χωρίζονται σε
παράλληλο, αδιέξοδο (διακλαδισμένο),
δακτυλιοειδείς (κλειστοί) αγωγοί,
εντάσσεται στο δίκτυο ύδρευσης.
Υδραυλικός
ο υπολογισμός του αγωγού μειώνεται ως
συνήθως για την επίλυση τριών βασικών προβλημάτων:
-
ορισμός
ροή αγωγού Q,
αν είναι γνωστό
πίεση H,
μήκος μεγάλο
και διάμετρο ρε
αγωγός,
δεδομένης της διαθεσιμότητας ορισμένων τοπικών
αντιστάσεις ή απουσία τους. -
ορισμός
απαιτούμενη πίεση H,
απαραίτητο για την εξασφάλιση μιας πάσας
γνωστή ροή Q
με αγωγό
μήκος μεγάλο
και διάμετρο ρε; -
ορισμός
διάμετρος αγωγού ρε
πότε
γνωστές τιμές κεφαλής H,
δαπάνη Q
και μήκος μεγάλο.
Ο ρυθμός ροής του υγρού είναι
όπου q > ροή ρευστού σχεδιασμού, m3/s;
- περιοχή του ενεργού τμήματος του σωλήνα, m2.
Ο συντελεστής αντίστασης τριβής λ προσδιορίζεται σύμφωνα με τους κανονισμούς του συνόλου κανόνων SP 40-102-2000 «Σχεδιασμός και εγκατάσταση αγωγών για συστήματα ύδρευσης και αποχέτευσης από πολυμερή υλικά. Γενικές Προϋποθέσεις":
όπου b είναι κάποιος αριθμός ομοιότητας των καθεστώτων ροής ρευστού. για b > 2, λαμβάνεται b = 2.
όπου Re είναι ο πραγματικός αριθμός Reynolds.
όπου ν είναι ο συντελεστής κινηματικού ιξώδους του υγρού, m²/s. Κατά τον υπολογισμό των σωλήνων κρύου νερού, λαμβάνεται ίσο με 1,31 10-6 m² / s - το ιξώδες του νερού σε θερμοκρασία +10 ° C.
Rekv > - Αριθμός Reynolds που αντιστοιχεί στην αρχή της τετραγωνικής περιοχής της υδραυλικής αντίστασης.
όπου Ke είναι η υδραυλική τραχύτητα του υλικού του σωλήνα, m. Για σωλήνες από πολυμερή υλικά, λαμβάνεται Ke = 0,00002 m εάν ο κατασκευαστής του σωλήνα δεν δώσει άλλες τιμές τραχύτητας.
Σε εκείνες τις περιπτώσεις ροής όταν Re ≥ Rekv, η υπολογισμένη τιμή της παραμέτρου b γίνεται ίση με 2 και ο τύπος (4) απλοποιείται σημαντικά, μετατρέποντας τον γνωστό τύπο Prandtl:
Στο Ke = 0,00002 m, η περιοχή τετραγωνικής αντίστασης εμφανίζεται με ρυθμό ροής νερού (ν = 1,31 10-6 m²/s) ίσο με 32,75 m/s, ο οποίος είναι πρακτικά ανέφικτος στα δημόσια συστήματα ύδρευσης.
Για καθημερινούς υπολογισμούς, συνιστώνται νομογράμματα και για πιο ακριβείς υπολογισμούς - "Πίνακες για υδραυλικούς υπολογισμούς αγωγών από πολυμερή υλικά", τόμος 1 "Σωληνώσεις πίεσης" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
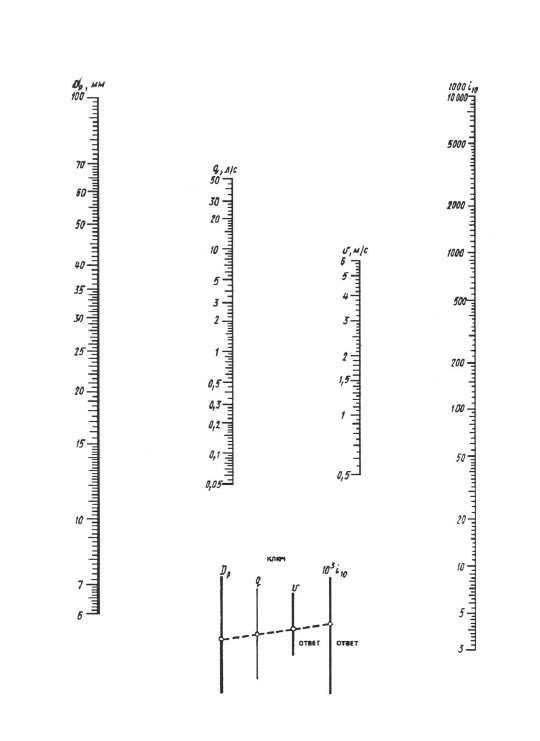
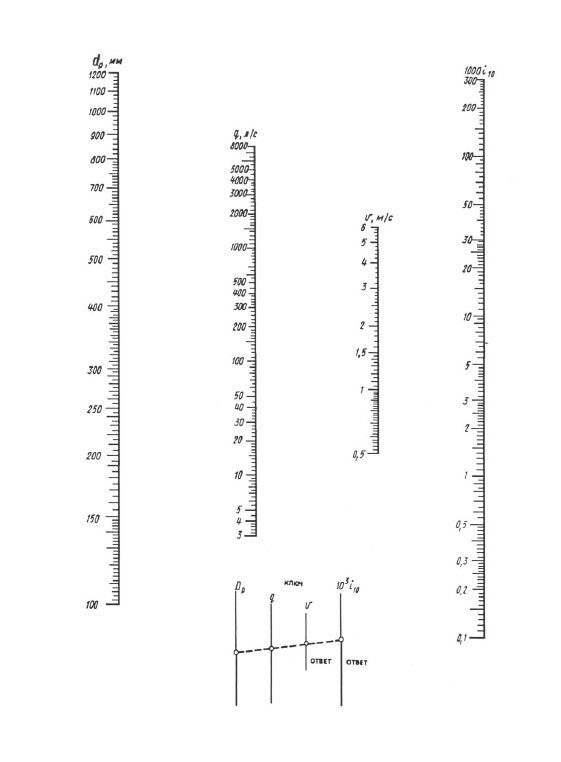
Κατά τον υπολογισμό σύμφωνα με νομογράμματα, το αποτέλεσμα επιτυγχάνεται με μία επικάλυψη του χάρακα - θα πρέπει να συνδέσετε το σημείο με την τιμή της υπολογισμένης διαμέτρου στην κλίμακα dp με το σημείο με την τιμή του υπολογισμένου ρυθμού ροής στο q (l / ιθ) κλίμακα με ευθεία γραμμή, συνεχίστε αυτή την ευθεία μέχρι να τέμνεται με τις κλίμακες της ταχύτητας V και των ειδικών απωλειών κεφαλή 1000 i (mm/m). Τα σημεία τομής μιας ευθείας με αυτές τις κλίμακες δίνουν την τιμή V και 1000 i.
Όπως γνωρίζετε, το κόστος της ηλεκτρικής ενέργειας για την άντληση υγρού είναι ευθέως ανάλογο με την τιμή του H (ceteris paribus). Αντικαθιστώντας την έκφραση ( 3 ) στον τύπο ( 2 ), είναι εύκολο να δούμε ότι η τιμή του i (και, κατά συνέπεια, του H) είναι αντιστρόφως ανάλογη με την υπολογισμένη διάμετρο dp στον πέμπτο βαθμό.
Δείχνεται παραπάνω ότι η τιμή της dp εξαρτάται από το πάχος του τοιχώματος του σωλήνα e: όσο πιο λεπτό είναι το τοίχωμα, τόσο μεγαλύτερη είναι η dp και, κατά συνέπεια, τόσο μικρότερη είναι η απώλεια πίεσης λόγω τριβής και το κόστος ηλεκτρικής ενέργειας.
Εάν η τιμή MRS του σωλήνα αλλάξει για οποιονδήποτε λόγο, πρέπει να υπολογιστεί εκ νέου η διάμετρος και το πάχος του τοιχώματος (SDR).
Θα πρέπει να ληφθεί υπόψη ότι σε ορισμένες περιπτώσεις η χρήση σωλήνων με MRS 10 αντί για σωλήνες με MRS 8, ειδικά σωλήνων με MRS 6.3, καθιστά δυνατή τη μείωση της διαμέτρου του αγωγού κατά ένα μέγεθος. Επομένως, στην εποχή μας, η χρήση πολυαιθυλενίου PE 80 (MRS 8) και PE 100 (MRS 10) αντί πολυαιθυλενίου PE 63 (MRS 6.3) για την κατασκευή σωλήνων επιτρέπει όχι μόνο τη μείωση του πάχους τοιχώματος των σωλήνων, αλλά και του βάρους τους και κατανάλωση υλικών, αλλά και για μείωση του ενεργειακού κόστους για την άντληση υγρού (ceteris paribus).
Τα τελευταία χρόνια (μετά το 2013), οι σωλήνες από πολυαιθυλένιο PE80 έχουν σχεδόν πλήρως αντικατασταθεί από την παραγωγή από σωλήνες από πολυαιθυλένιο ποιότητας PE100. Αυτό εξηγείται από το γεγονός ότι οι πρώτες ύλες από τις οποίες κατασκευάζονται οι σωλήνες προμηθεύονται από το εξωτερικό με το σήμα PE100.Και επίσης το γεγονός ότι η κατηγορία πολυαιθυλενίου 100 έχει περισσότερα χαρακτηριστικά αντοχής, λόγω των οποίων παράγονται σωλήνες με τα ίδια χαρακτηριστικά με τους σωλήνες από PE80, αλλά με λεπτότερο τοίχωμα, αυξάνοντας έτσι την απόδοση των αγωγών πολυαιθυλενίου.
Νομόγραμμα για τον προσδιορισμό των απωλειών πίεσης σε σωλήνες με διάμετρο 6, 100 mm.
Νομόγραμμα για τον προσδιορισμό των απωλειών πίεσης σε σωλήνες με διάμετρο 100, 1200 mm.
Κριτήριο Reynolds
Αυτή η εξάρτηση αναδείχθηκε από τον Άγγλο φυσικό και μηχανικό Osborne Reynolds (1842-1912).
Το κριτήριο που βοηθά στην απάντηση στο ερώτημα εάν υπάρχει ανάγκη να ληφθεί υπόψη το ιξώδες είναι ο αριθμός Reynolds Re. Είναι ίσος με τον λόγο της ενέργειας κίνησης ενός στοιχείου ενός ρέοντος ρευστού προς το έργο των εσωτερικών δυνάμεων τριβής.
Θεωρήστε ένα κυβικό ρευστό στοιχείο με μήκος ακμής n. Η κινητική ενέργεια ενός στοιχείου είναι:
Σύμφωνα με το νόμο του Νεύτωνα, η δύναμη τριβής που ασκείται σε ένα ρευστό στοιχείο ορίζεται ως εξής:
Το έργο αυτής της δύναμης όταν κινείται ένα ρευστό στοιχείο σε απόσταση n είναι
και ο λόγος της κινητικής ενέργειας του ρευστού στοιχείου προς το έργο της δύναμης τριβής είναι
Μειώνουμε και παίρνουμε:
Το Re ονομάζεται αριθμός Reynolds.
Έτσι, το Re είναι ένα αδιάστατο μέγεθος που χαρακτηρίζει τον σχετικό ρόλο των ιξωδών δυνάμεων.
Για παράδειγμα, εάν οι διαστάσεις του σώματος με το οποίο έρχεται σε επαφή το υγρό ή το αέριο είναι πολύ μικρές, τότε ακόμη και με μικρό ιξώδες, το Re θα είναι ασήμαντο και οι δυνάμεις τριβής παίζουν κυρίαρχο ρόλο. Αντίθετα, αν οι διαστάσεις του σώματος και η ταχύτητα είναι μεγάλες, τότε το Re >> 1 και ακόμη και ένα μεγάλο ιξώδες δεν θα έχουν σχεδόν καμία επίδραση στη φύση της κίνησης.
Ωστόσο, οι υψηλοί αριθμοί Reynolds δεν σημαίνουν πάντα ότι το ιξώδες δεν παίζει κανένα ρόλο. Έτσι, όταν επιτευχθεί μια πολύ μεγάλη (πολλές δεκάδες ή εκατοντάδες χιλιάδες) τιμή του αριθμού Re, μια ομαλή στρωτή ροή (από το λατινικό lamina - «πλάκα») μετατρέπεται σε τυρβώδη (από το λατινικό turbulentus - «θυελλώδης» , «χαοτικό»), συνοδευόμενο από χαοτικές, ασταθείς κινήσεις υγρών. Αυτό το φαινόμενο μπορεί να παρατηρηθεί εάν ανοίξετε σταδιακά μια βρύση: ένα λεπτό ρεύμα συνήθως ρέει ομαλά, αλλά με την αύξηση της ταχύτητας του νερού, η ομαλότητα της ροής διαταράσσεται. Σε έναν πίδακα που ρέει έξω υπό υψηλή πίεση, τα σωματίδια υγρού κινούνται τυχαία, ταλαντευόμενα, κάθε κίνηση συνοδεύεται από ισχυρή ανάμειξη.
Η εμφάνιση αναταράξεων αυξάνει σημαντικά την αντίσταση. Σε έναν αγωγό, η ταχύτητα τυρβώδους ροής είναι μικρότερη από την ταχύτητα στρωτής ροής στις ίδιες πτώσεις πίεσης. Αλλά οι αναταράξεις δεν είναι πάντα κακές. Λόγω του γεγονότος ότι η ανάμειξη κατά τη διάρκεια των αναταράξεων είναι πολύ σημαντική, η μεταφορά θερμότητας - ψύξη ή θέρμανση αδρανών - συμβαίνει πολύ πιο εντατικά. η εξάπλωση των χημικών αντιδράσεων είναι ταχύτερη.
Η Εξίσωση Σταθερής Κίνησης του Bernoulli
Μία από τις σημαντικότερες εξισώσεις της υδρομηχανικής ελήφθη το 1738 από τον Ελβετό επιστήμονα Daniel Bernoulli (1700-1782). Ήταν ο πρώτος που περιέγραψε την κίνηση ενός ιδανικού ρευστού, που εκφράζεται με τον τύπο Bernoulli.
Ιδανικό ρευστό είναι ένα ρευστό στο οποίο δεν υπάρχουν δυνάμεις τριβής μεταξύ των στοιχείων ενός ιδανικού ρευστού, καθώς και μεταξύ του ιδανικού ρευστού και των τοιχωμάτων του δοχείου.
Η εξίσωση ακίνητης κίνησης που φέρει το όνομά του είναι:
όπου P είναι η πίεση του υγρού, ρ η πυκνότητά του, v η ταχύτητα κίνησης, g η επιτάχυνση της ελεύθερης πτώσης, h το ύψος στο οποίο βρίσκεται το στοιχείο του υγρού.
Η έννοια της εξίσωσης Bernoulli είναι ότι μέσα σε ένα σύστημα γεμάτο υγρό (τμήμα αγωγού) η συνολική ενέργεια κάθε σημείου είναι πάντα αμετάβλητη.
Η εξίσωση Bernoulli έχει τρεις όρους:
- ρ⋅v2/2 - δυναμική πίεση - κινητική ενέργεια ανά μονάδα όγκου του κινητήριου ρευστού.
- ρ⋅g⋅h - πίεση βάρους - δυναμική ενέργεια ανά μονάδα όγκου υγρού.
- P - η στατική πίεση, στην αρχή της είναι το έργο των δυνάμεων πίεσης και δεν αντιπροσωπεύει απόθεμα κάποιου ειδικού τύπου ενέργειας («ενέργεια πίεσης»).
Αυτή η εξίσωση εξηγεί γιατί σε στενά τμήματα του σωλήνα η ταχύτητα ροής αυξάνεται και η πίεση στα τοιχώματα του σωλήνα μειώνεται. Η μέγιστη πίεση στους σωλήνες ρυθμίζεται ακριβώς στο σημείο όπου ο σωλήνας έχει τη μεγαλύτερη διατομή. Τα στενά μέρη του σωλήνα είναι ασφαλή από αυτή την άποψη, αλλά η πίεση σε αυτά μπορεί να πέσει τόσο πολύ ώστε το υγρό να βράσει, γεγονός που μπορεί να οδηγήσει σε σπηλαίωση και καταστροφή του υλικού του σωλήνα.
Εξίσωση Navier-Stokes για παχύρρευστα υγρά
Σε μια πιο αυστηρή διατύπωση, η γραμμική εξάρτηση της ιξώδους τριβής από την αλλαγή στην ταχύτητα του ρευστού ονομάζεται εξίσωση Navier-Stokes. Λαμβάνει υπόψη τη συμπιεστότητα υγρών και αερίων και, σε αντίθεση με το νόμο του Νεύτωνα, ισχύει όχι μόνο κοντά στην επιφάνεια ενός στερεού σώματος, αλλά και σε κάθε σημείο του υγρού (κοντά στην επιφάνεια ενός στερεού σώματος στην περίπτωση ενός ασυμπίεστου υγρό, η εξίσωση Navier-Stokes και ο νόμος του Νεύτωνα συμπίπτουν).
Οποιαδήποτε αέρια για τα οποία ικανοποιείται η συνθήκη ενός συνεχούς μέσου υπακούουν επίσης στην εξίσωση Navier-Stokes, δηλ. είναι νευτώνεια ρευστά.
Το ιξώδες των υγρών και των αερίων είναι συνήθως σημαντικό σε σχετικά χαμηλές ταχύτητες, επομένως μερικές φορές λέγεται ότι η υδροδυναμική του Euler είναι μια ειδική (περιοριστική) περίπτωση υψηλών ταχυτήτων της υδροδυναμικής Navier-Stokes.
Σε χαμηλές ταχύτητες, σύμφωνα με το νόμο του Νεύτωνα για την ιξώδη τριβή, η δύναμη έλξης του σώματος είναι ανάλογη της ταχύτητας. Στις υψηλές ταχύτητες, όταν το ιξώδες παύει να παίζει σημαντικό ρόλο, η αντίσταση του σώματος είναι ανάλογη του τετραγώνου της ταχύτητας (που ανακαλύφθηκε και τεκμηριώθηκε για πρώτη φορά από τον Νεύτωνα).
Ακολουθία Υδραυλικού Υπολογισμού
1.
Επιλέγεται η κύρια κυκλοφορία
σύστημα θέρμανσης δακτυλίου (τα περισσότερα
βρίσκεται σε μειονεκτική θέση στο υδραυλικό
σχέση). Σε αδιέξοδο δισωλήνιο
συστήματα είναι ένας δακτύλιος που διέρχεται
κατώτερο όργανο του πιο απομακρυσμένου και
φορτωμένος ανυψωτήρας, σε μονοσωλήνιο -
μέσω των πιο απομακρυσμένων και φορτωμένων
υψών.
Για παράδειγμα,
σε σύστημα θέρμανσης δύο σωλήνων με
άνω καλωδίωση κύρια κυκλοφορία
ο δακτύλιος θα περάσει από το σημείο θερμότητας
μέσω της κύριας ανύψωσης, γραμμής τροφοδοσίας,
μέσω του πιο απομακρυσμένου ανυψωτικού, θέρμανσης
κάτω συσκευή, γραμμή επιστροφής
στο σημείο θέρμανσης.
V
συστήματα με σχετική κίνηση του νερού μέσα
το δαχτυλίδι λαμβάνεται ως το κύριο,
περνώντας από τη μέση περισσότερο
φορτωμένη βάση.
2.
Ο κύριος δακτύλιος κυκλοφορίας σπάει
σε οικόπεδα (η πλοκή χαρακτηρίζεται
σταθερή ροή νερού και το ίδιο
διάμετρος). Το διάγραμμα δείχνει
αριθμούς τομέων, τα μήκη και τη θερμική τους
φορτία. Θερμικό φορτίο κύριας
τα οικόπεδα καθορίζονται με άθροιση
θερμικά φορτία που εξυπηρετούνται από αυτά
οικόπεδα. Για να επιλέξετε διάμετρο σωλήνα
χρησιμοποιούνται δύο ποσότητες:
ένα)
δεδομένης ροής νερού.
σι)
κατά προσέγγιση ειδικές απώλειες πίεσης
για τριβή στην κυκλοφορία σχεδίασης
δαχτυλίδι RΝυμφεύω.
Για
υπολογισμός Rcp
πρέπει να γνωρίζουμε το μήκος του κύριου
δακτύλιος κυκλοφορίας και υπολογίζεται
πίεση κυκλοφορίας.
3.
Η υπολογισμένη κυκλοφορία
πίεση τύπου
 ,
,
(5.1)
που
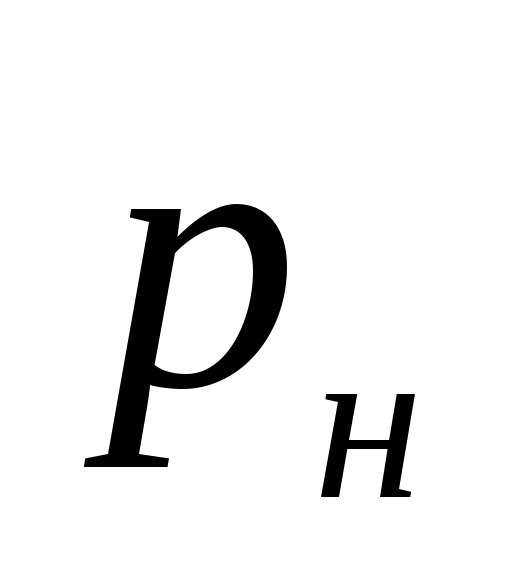
πίεση που δημιουργείται από την αντλία, Pa.
Πρακτική Σχεδιασμού Συστήματος
θέρμανση έδειξε ότι τα περισσότερα
συνιστάται η λήψη της πίεσης της αντλίας,
ίσος
 ,
,
(5.2)
που
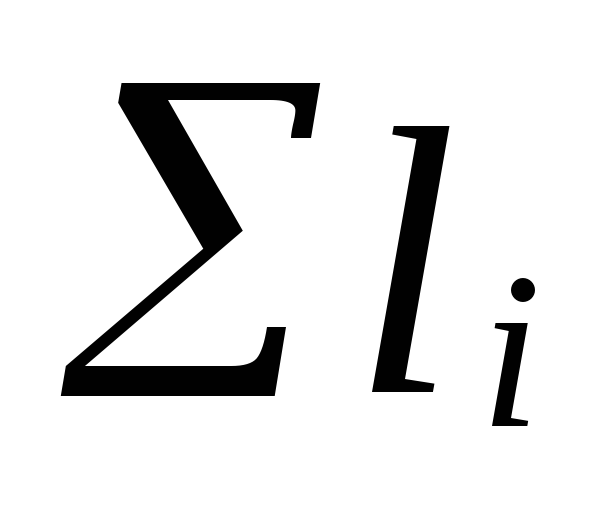
το άθροισμα των μηκών των τμημάτων της κύριας κυκλοφορίας
δαχτυλίδια?
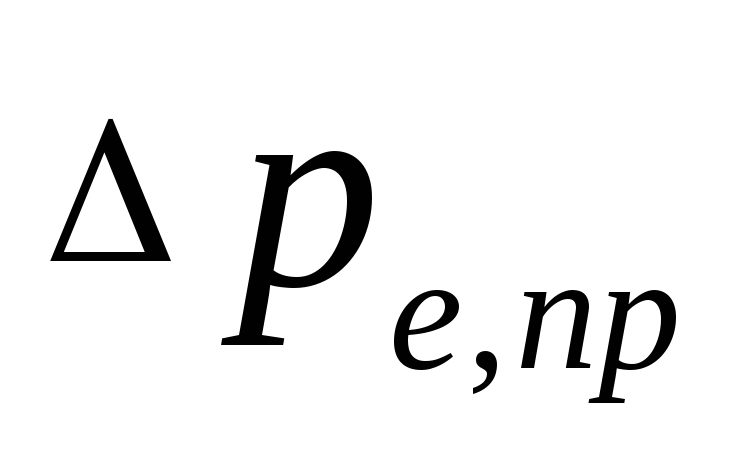
φυσική πίεση που εμφανίζεται όταν
υδρόψυξη σε συσκευές, Pa, δυνατή
καθορίσει πώς
 ,
,
(5.3)
που
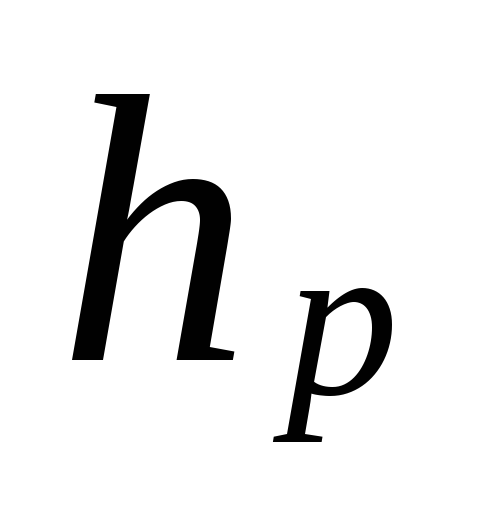
απόσταση από το κέντρο της αντλίας (ασανσέρ)
στο κέντρο της συσκευής του κάτω ορόφου, m.
Εννοια
συντελεστής δυνατό
καθορίστε από τον Πίνακα 5.1.
τραπέζι
5.1 - Σημασία γ
ανάλογα με τη θερμοκρασία σχεδιασμού
νερό στο σύστημα θέρμανσης
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
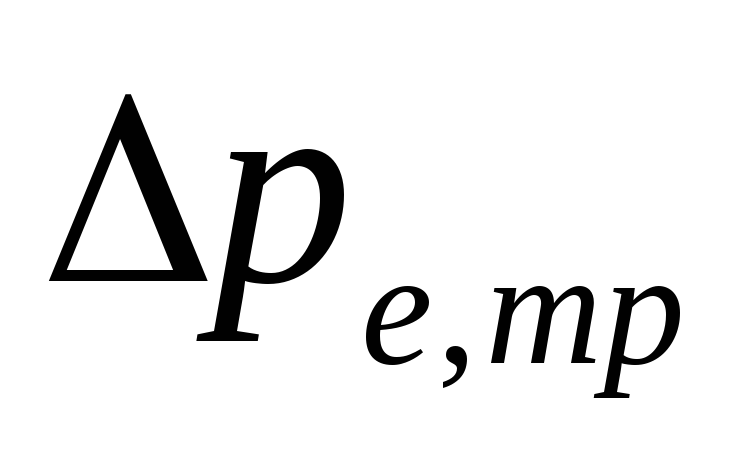
φυσική πίεση σε
ως αποτέλεσμα της ψύξης του νερού σε αγωγούς
.
V
συστήματα άντλησης με καλωδίωση στο κάτω μέρος
μέγεθος
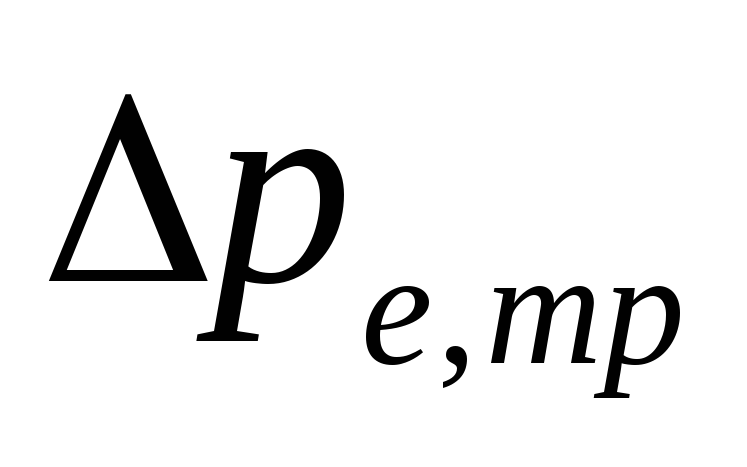
-
Αποφασίζονται
ειδική απώλεια πίεσης τριβής
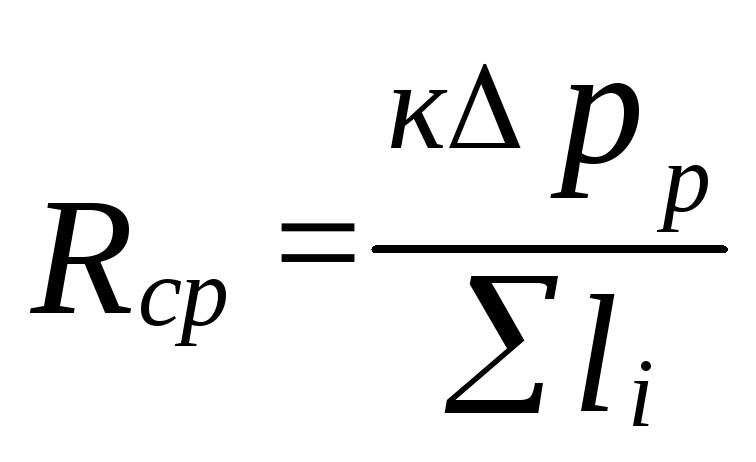
(5.4)
που
Το k=0,65 καθορίζει την αναλογία των απωλειών πίεσης
για τριβή.
5.
Η κατανάλωση νερού στην τοποθεσία καθορίζεται από
τύπος
 (5.5)
(5.5)
που
Q
- θερμικό φορτίο στην τοποθεσία, W:
(τσολ
— τΟ)
- διαφορά θερμοκρασίας του ψυκτικού.
6.
Κατά μέγεθος
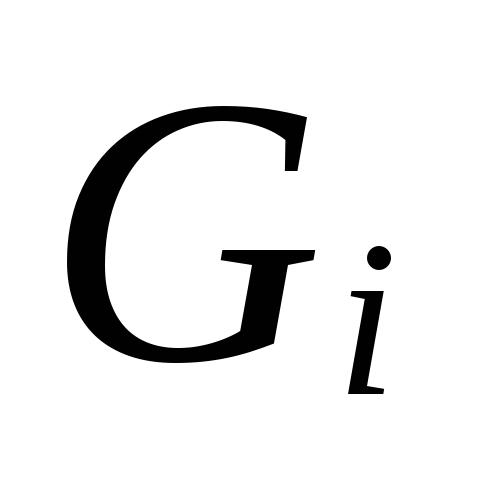
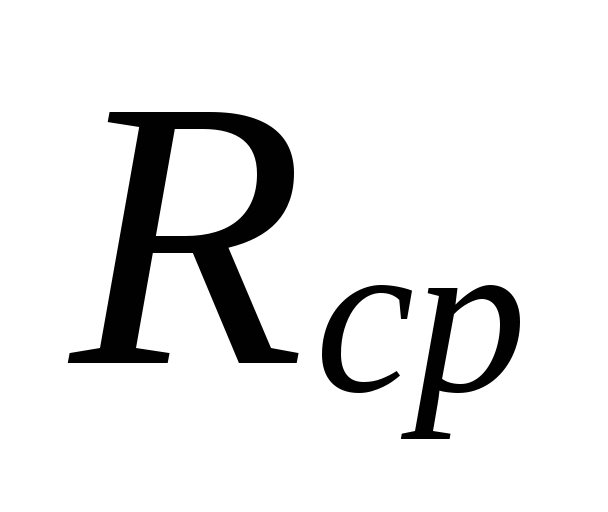
.

6.
Για επιλεγμένες διαμέτρους αγωγών
και προσδιορίζεται η εκτιμώμενη κατανάλωση νερού
ταχύτητα ψυκτικού v
και το πραγματικό συγκεκριμένο
απώλεια πίεσης τριβής Rφά.
Στο
επιλογή διαμέτρων σε περιοχές με μικρές
οι ρυθμοί ροής ψυκτικού υγρού μπορεί να είναι
μεγάλες αποκλίσεις μεταξύ
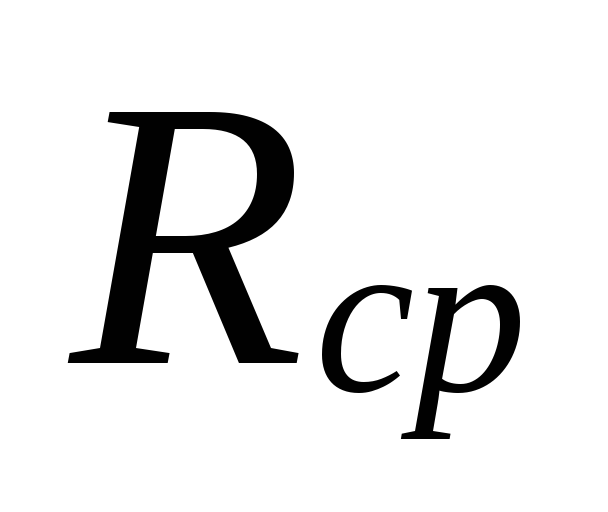
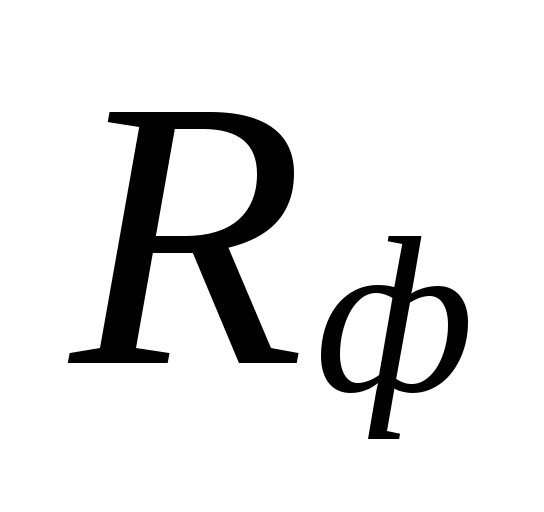
υποτιμημένες απώλειες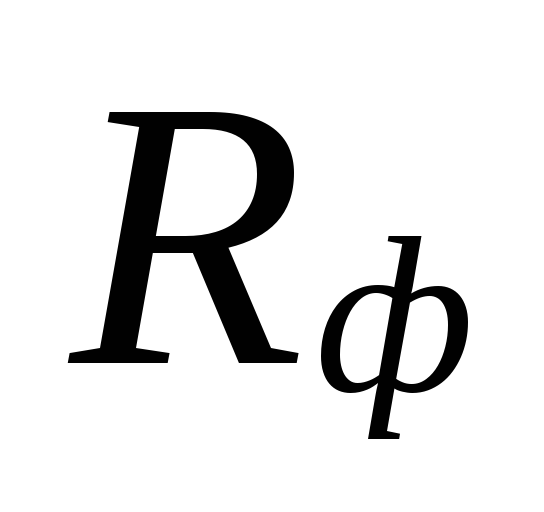
αυτές οι περιοχές αντισταθμίζονται από υπερεκτίμηση
ποσότητες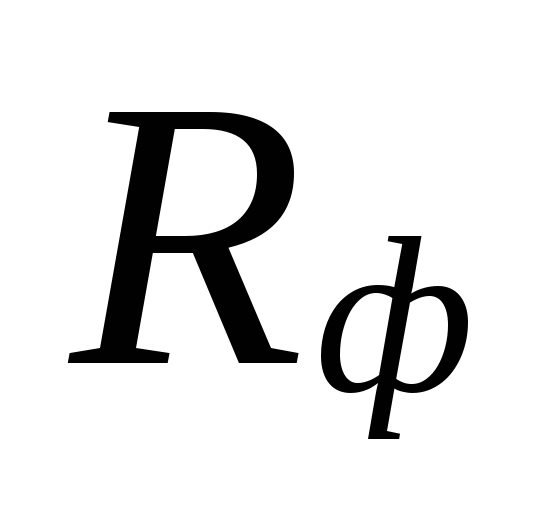
7.
Προσδιορίζονται οι απώλειες πίεσης τριβής
στην υπολογιζόμενη περιοχή, Pa:
 .
.
(5.6)
Αποτελέσματα
Οι υπολογισμοί καταχωρούνται στον Πίνακα 5.2.
8.
Απώλειες πίεσης σε τοπικό επίπεδο
αντιστάσεις χρησιμοποιώντας είτε τον τύπο:
 ,
,
(5.7)
που
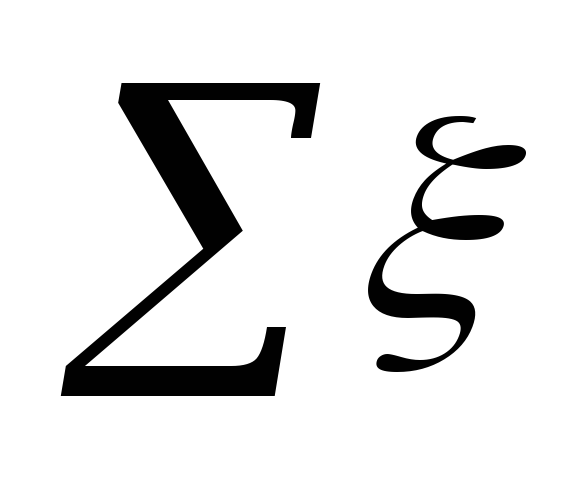
στην περιοχή του οικισμού.
Εννοια ξ
σε κάθε τοποθεσία συνοψίζονται στον πίνακα. 5.3.
Πίνακας 5.3 -
Τοπικοί συντελεστές αντίστασης
|
Αρ. p / p |
Ονόματα |
Αξίες |
Σημειώσεις |
9.
Προσδιορίστε τη συνολική απώλεια πίεσης
σε κάθε περιοχή
 .
.
(5.8)
10. Προσδιορίστε
συνολική απώλεια πίεσης λόγω τριβής και
σε τοπικές αντιστάσεις κατά κύριο λόγο
δακτύλιος κυκλοφορίας
 .
.
(5.9)
11. Συγκρίνετε Δρ
Με ΔρR.
Ολική απώλεια πίεσης σε όλο τον δακτύλιο
πρέπει να είναι μικρότερο από ΔρR
στο
 .
.
(5.10)
απόθεμα μιας χρήσης
Απαιτείται πίεση σε ασύλληπτα in
υπολογισμός της υδραυλικής αντίστασης.
Εάν δεν υπάρχουν προϋποθέσεις
εκτελούνται, είναι απαραίτητο σε ορισμένους
τμήματα του δακτυλίου για να αλλάξετε τις διαμέτρους των σωλήνων.
12. Μετά τον υπολογισμό
κύριος δακτύλιος κυκλοφορίας
κάντε τη σύνδεση των υπόλοιπων δακτυλίων. V
κάθε νέο δαχτυλίδι μετράει μόνο
επιπλέον μη κοινόχρηστοι χώροι,
συνδέονται παράλληλα με τμήματα
κύριος δακτύλιος.
Ασυμφωνία απώλειας
πιέσεις σε παράλληλη σύνδεση
επιτρεπόμενα οικόπεδα έως 15% με αδιέξοδο
η κίνηση του νερού και έως και 5% - με πέρασμα.
τραπέζι
5.2 - Αποτελέσματα υδραυλικού υπολογισμού
για σύστημα θέρμανσης
|
Στο |
Με |
Με |
||||||||||||||
|
Αριθμός |
θερμικός |
Κατανάλωση |
Μήκος |
Διάμετρος |
Ταχύτητα |
Ειδικός |
Απώλειες |
Αθροισμα |
Απώλειες |
ρε, |
v, |
R, |
Δρtr, |
∑ξ |
Ζ, |
Rl+Ζ, |
Μάθημα 6
Αλλαγή της θερμοκρασίας του αερίου κατά μήκος του αγωγού αερίου
Σε σταθερή ροή αερίου, η μάζα
ο ρυθμός ροής στον αγωγό αερίου είναι
 . (2.41)
. (2.41)
Στην πραγματικότητα, η κίνηση του φυσικού αερίου στον αγωγό αερίου
είναι πάντα μη ισοθερμικό. V
Κατά τη συμπίεση, το αέριο θερμαίνεται.
Ακόμα και μετά την ψύξη του στο COP, η θερμοκρασία
αερίου που εισέρχεται στον αγωγό
είναι περίπου 2040С,
που είναι πολύ υψηλότερη από τη θερμοκρασία
περιβάλλον (Τ).
Στην πράξη, η θερμοκρασία του αερίου γίνεται
κοντά στη θερμοκρασία περιβάλλοντος
μόνο για αγωγούς αερίου μικρής διαμέτρου
(Dy0.
Επιπλέον, θα πρέπει να ληφθεί υπόψη ότι
αερίου με αγωγούς
είναι ένα πραγματικό αέριο, το οποίο είναι εγγενές
το φαινόμενο Joule-Thompson, το οποίο λαμβάνει υπόψη
απορρόφηση θερμότητας κατά τη διαστολή αερίου.
Όταν η θερμοκρασία αλλάζει κατά μήκος
περιγράφεται η κίνηση αερίου του αγωγού αερίου
σύστημα εξισώσεων:
συγκεκριμένη ενέργεια ,
,
συνέχεια ,
,
πολιτείες ,
,
ισορροπία θερμότητας .
.
Θεωρήστε στην πρώτη προσέγγιση την εξίσωση
ισορροπία θερμότητας χωρίς να λαμβάνεται υπόψη η επίδραση
Joule Thompson. Ολοκλήρωση της εξίσωσης
ισορροπία θερμότητας
 ,
,
παίρνουμε
 , (2.42)
, (2.42)
που ;
;
κSR- κατά μέσο όρο στον ιστότοπο πλήρης
συντελεστής μεταφοράς θερμότητας από αέριο σε
περιβάλλον;
G είναι ο ρυθμός ροής μάζας του αερίου.
ντοΠ–
μέση ισοβαρική θερμοχωρητικότητα του αερίου.
μια αξίαtL ονομάζεται το αδιάστατο κριτήριο
Σούχοφ
 (2.43)
(2.43)
Άρα η θερμοκρασία του αερίου στο τέλος
αγωγός φυσικού αερίου θα είναι
 . (2.44)
. (2.44)
Σε απόσταση x από την αρχή
προσδιορίζεται η θερμοκρασία αερίου του αγωγού αερίου
σύμφωνα με τον τύπο
 . (2.45)
. (2.45)
Αλλαγή θερμοκρασίας σε όλο το μήκος του αγωγού αερίου
είναι εκθετική (Εικ.
2.6).
Σκεφτείτε
επίδραση της αλλαγής της θερμοκρασίας του αερίου σε
απόδοση του αγωγού.
Πολλαπλασιάζοντας και τις δύο πλευρές της συγκεκριμένης εξίσωσης
ενέργεια στο 2 και εκφράζοντας ,
,
παίρνουμε
 . (2.46)
. (2.46)
Εκφράζουμε την πυκνότητα του αερίου στην αριστερή πλευρά
εκφράσεις (2.46) από την εξίσωση κατάστασης
 ,
,
γινόμενοwαπό την εξίσωση συνέχειας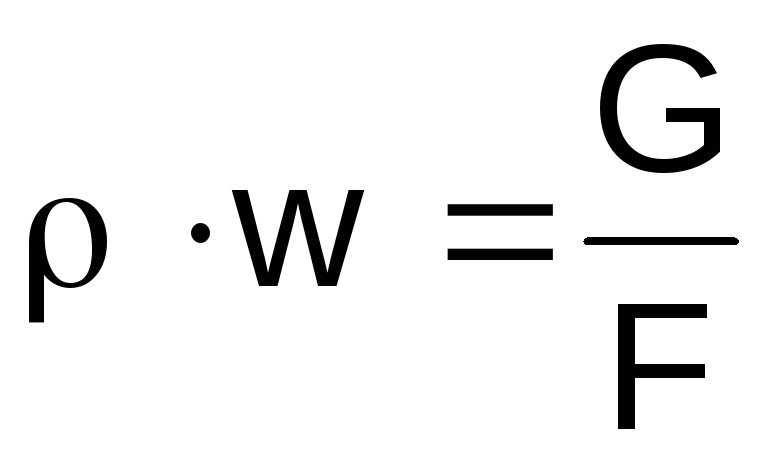
ισορροπία .
.
Έχοντας αυτό υπόψη, η συγκεκριμένη εξίσωση
η ενέργεια παίρνει τη μορφή
 (2.47)
(2.47)
ή
 . (2.48)
. (2.48)
Δηλώνοντας
 και ενσωματώνοντας την αριστερή πλευρά της εξίσωσης
και ενσωματώνοντας την αριστερή πλευρά της εξίσωσης
(2,48) από τον ΠHdoPΠΡΟΣ ΤΟ, και δεξιά από το ΤHτελείαΠΡΟΣ ΤΟ, παίρνουμε
 . (2.49)
. (2.49)
Με αντικατάσταση
 , (2.50)
, (2.50)
έχουμε
 . (2.51)
. (2.51)
Μετά την ενσωμάτωση στο καθορισμένο
όρια, έχουμε

 . (2.52)
. (2.52)
Λαμβάνοντας υπόψη το (2.42)

ή
 , (2.53)
, (2.53)
που είναι ένας διορθωτικός παράγοντας που λαμβάνει υπόψη
είναι ένας διορθωτικός παράγοντας που λαμβάνει υπόψη
αλλαγή θερμοκρασίας κατά μήκος του αγωγού αερίου
(μη ισοθερμικότητα της ροής του αερίου).
Λαμβάνοντας υπόψη το (2.53), την εξάρτηση για τον προσδιορισμό
ο ρυθμός ροής μάζας του αερίου θα λάβει τη μορφή
 . (2.54)
. (2.54)
Αξία Hπάντα μεγαλύτερο από ένα, έτσι
ρυθμός ροής μάζας αερίου κατά την αλλαγή
θερμοκρασία σε όλο το μήκος του αγωγού αερίου
(καθεστώς μη ισοθερμικής ροής) πάντα
λιγότερο από ό,τι σε ισοθερμική λειτουργία
(T=idem). Προϊόν THονομάζεται μέσο ολοκλήρωμα
θερμοκρασία του αερίου στον αγωγό.
Με τις τιμές του αριθμού Shukhov Shu4
ροή αερίου στον αγωγό
θεωρούν σχεδόν ισοθερμική
στο T=idem. Τέτοια θερμοκρασία
η λειτουργία είναι δυνατή κατά την άντληση αερίου με
χαμηλό κόστος αγωγών φυσικού αερίου
μικρή (λιγότερη από 500 mm) διάμετρο έως σημαντική
απόσταση.
Επίδραση της αλλαγής της θερμοκρασίας του αερίου
εκδηλώνεται για τις τιμές του αριθμού Shukhov
Shu
Στο
άντληση αερίου παρουσία γκαζιού
αποτέλεσμα οδηγεί σε μια βαθύτερη
ψύξη αερίου παρά μόνο με εναλλαγή θερμότητας
με χώμα. Σε αυτή την περίπτωση η θερμοκρασία
το αέριο μπορεί να πέσει ακόμη και κάτω
θερμοκρασία T (Εικ.
2.7).
Ρύζι. 2.7. Επιρροή του φαινομένου Joule-Thompson
στην κατανομή θερμοκρασίας αερίου πάνω
μήκος αγωγού
1 - χωρίς να λαμβάνεται υπόψη ο Di. 2 - με
λαμβάνοντας υπόψη τον Δι
Στη συνέχεια, λαμβάνοντας υπόψη τον συντελεστή Joule-Thompson
νόμος της μεταβολής της θερμοκρασίας κατά μήκος
παίρνει τη μορφή
 , (2.55)
, (2.55)
5 Υδραυλικές απώλειες
Διαφορά
πίεση λαδιού σε δύο τμήματα του ενός
και του ίδιου αγωγού, υπό την προϋπόθεση ότι
το πρώτο βρίσκεται ανάντη, και
το δεύτερο - παρακάτω, καθορίζεται εξίσωση
Μπερνούλι
 ,
,
που
η2
– η1
- η διαφορά στα ύψη των κέντρων βάρους
τμήματα από ένα αυθαίρετα επιλεγμένο
οριζόντιο επίπεδο?
v1,
v2
– μέσες ταχύτητες λαδιού σε τμήματα.
g - επιτάχυνση δύναμης
βαρύτητα;

υδραυλικές απώλειες κατά την κίνηση
λάδια από το πρώτο τμήμα στο δεύτερο.
Η εξίσωση
Bernoulli σε πλήρη χρήση
για τον υπολογισμό των γραμμών αναρρόφησης των αντλιών.
σε άλλες περιπτώσεις, τον πρώτο όρο,
συνήθως παραμελούνται και θεωρούνται:

υδραυλικός
οι απώλειες συνήθως χωρίζονται σε τοπικές
απώλειες και απώλειες τριβής κατά μήκος
αγωγοί (γραμμικοί).
1.5.1
τοπικές απώλειες
οι ενέργειες οφείλονται σε τοπικό
υδραυλική αντίσταση,
προκαλώντας παραμόρφωση ροής. Τοπικός
οι αντιστάσεις είναι: συστολές,
επέκταση, στρογγυλοποίηση αγωγών,
φίλτρα, εξοπλισμός ελέγχου και
ρύθμιση κλπ. Όταν ρέει
υγρών μέσω τοπικών αντιστάσεων
η ταχύτητά του αλλάζει και συνήθως υπάρχουν
μεγάλες δίνες.
Απώλειες
πίεση από τοπικές αντιστάσεις
καθορίζεται από τον τύπο Weisbach:
 MPa
MPa
(ή
 Pa),
Pa),
που

απώλεια,
v
είναι η μέση ταχύτητα ροής στη διατομή
σε σωλήνα πίσω από τοπική αντίσταση, m/s.
,
N/m3;
g=9,81 m/s2.
Καθε
χαρακτηρίζεται η τοπική αντίσταση
από την τιμή του συντελεστή του

Με τυρβώδη ροή, οι τιμές
αντίσταση και ελάχιστη αλλαγή
με αλλαγή στο μέγεθος του τμήματος, ταχύτητα
ροή ρευστού και ιξώδες. Έτσι
υποθέστε ότι δεν εξαρτώνται από τον αριθμό
Reynolds Re.
Αξίες

για παράδειγμα, για μπλουζάκια με το ίδιο
οι διάμετροι καναλιών λαμβάνονται ίσες,
αν:
ρέματα
αθροίζω, αποκλίνω? ροή
πέρασμα;









στο
κάμψη σωλήνα

Αξίες

σε υδραυλικά συστήματα εξοπλισμού, που λαμβάνονται από
βιβλιογραφία αναφοράς.
Στο
στρωτή ροή (Απ
Απώλειες
πίεση από τοπικές αντιστάσεις στο
η στρωτή ροή προσδιορίζονται από
τύπος:
 MPa
MPa
που

= α

Ποσότητες
απώλεια πίεσης στο τυπικό
υδραυλικές συσκευές για
ονομαστική ταχύτητα ροής συνήθως
αναφέρονται στις τεχνικές προδιαγραφές τους.
1.5.2
Απώλεια σε
τριβή μήκους
είναι η απώλεια ενέργειας που συμβαίνει
σε ευθύγραμμους σωλήνες σταθερής διατομής,
εκείνοι. με ομοιόμορφη ροή υγρού,
και αυξάνονται ανάλογα με το μήκος
σωλήνες. Οι απώλειες αυτές οφείλονται σε εσωτερικές
τριβή σε ένα υγρό, και ως εκ τούτου έχουν
τοποθετήστε σε τραχείς και λείους σωλήνες.
Απώλειες
πίεση τριβής αγωγού
καθορίζεται από τον τύπο Ντάρσυ:
 MPa
MPa
που

μεγάλο
και δ
- μήκος και εσωτερική διάμετρος του αγωγού,
mm.
Αυτό
ο τύπος ισχύει τόσο για στρωτή,
καθώς και σε τυρβώδη ροή? διαφορά
συνίσταται μόνο στις τιμές του συντελεστή

Στο
στρωτή ροή (Απ
Στο
συντελεστής τριβής τυρβώδους ροής
δεν είναι μόνο συνάρτηση του Re, αλλά
εξαρτάται επίσης από την τραχύτητα του εσωτερικού
επιφάνεια σωλήνα. Για υδραυλικά
λείος σωλήνες,
εκείνοι. με μια τραχύτητα που
πρακτικά δεν επηρεάζει την αντοχή του,
τυρβώδης συντελεστής τριβής
η λειτουργία μπορεί να προσδιοριστεί από τον τύπο Η/Υ.
Κονάκοβα:

σωλήνας
θεωρείται υδραυλικά λεία αν
(d/k)>(Re/20),
όπου k είναι η ισοδύναμη τραχύτητα,
mm. Για παράδειγμα, για νέο χάλυβα χωρίς ραφή
σωλήνες k≈0,03
mm, και μετά από αρκετά χρόνια λειτουργίας
k≈0,2
mm, για νέους σωλήνες χωρίς ραφή από
μη σιδηρούχα μέταλλα k≈0,005
mm. Αυτοί οι σωλήνες χρησιμοποιούνται συχνά σε
υδραυλικά συστήματα εργαλειομηχανών.
Συντελεστής
τριβή στο ταραχώδες καθεστώς μπορεί να είναι
προσδιορίστε με τύπο Altshulya,
είναι καθολική (δηλαδή εφαρμόσιμη
σε κάθε περίπτωση):

2. Χαρακτηριστικά ροής της μονάδας ροής αγωγού
Ας θυμηθούμε
τύπος γραμμικής απώλειας - τύπος Darcy
- Weisbach:
 .
.
Εξπρές
σε αυτόν τον τύπο, η ταχύτητα V
μέσω ροής Q
από την αναλογία
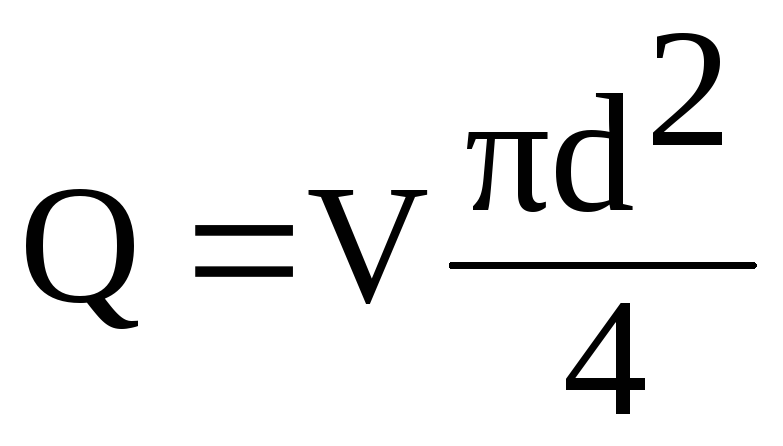
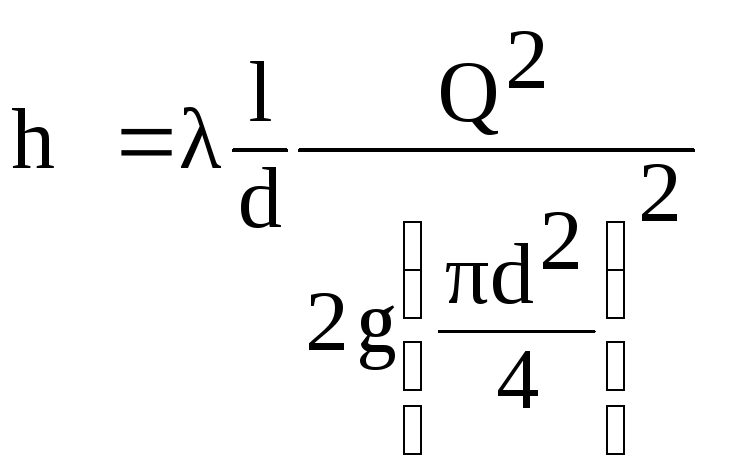
(6.1)
Για
αγωγός ορισμένης διαμέτρου
σύμπλεγμα ποσοτήτων
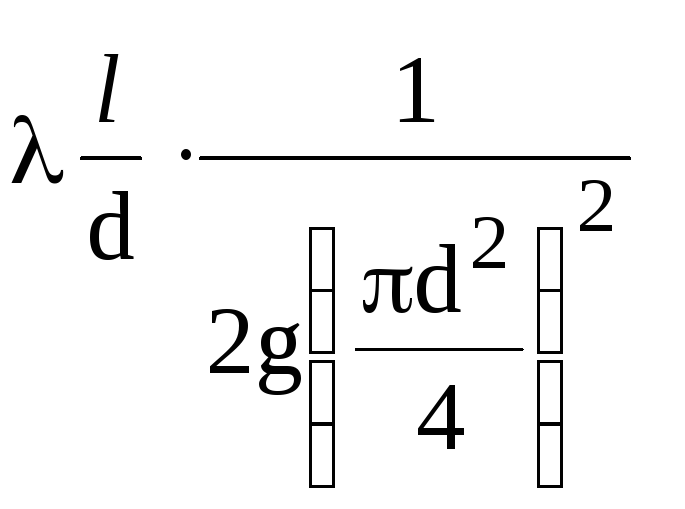
σταθερά (1/K2),
εκτός από τον υδραυλικό συντελεστή
τριβή λ. Με βάση την έννοια
μέση οικονομική ταχύτητα Vσ.ε
ας δείξουμε ότι ο υποδεικνυόμενος συντελεστής λ
μπορεί να αποδοθεί σε αυτό το σύμπλεγμα, γιατί v
Σε αυτήν την περίπτωση, ο αριθμός Reynolds θα είναι
έχουν συγκεκριμένη σημασία:
 ,
,
και στο οικόπεδο Nikuradze, ο συντελεστής λ in
αυτή η περίπτωση θα έχει μια συγκεκριμένη
έννοια.
Δικαιολογώ
νομιμότητα της εισαγωγής της έννοιας
μέση οικονομική ταχύτητα ως εξής
αιτιολογία.
υδραυλικός
σύστημα, όπως υδραυλικά,
μπορείτε να παραλείψετε μια συγκεκριμένη δαπάνη
κατασκευασμένο από σωλήνες διαφορετικών διαμέτρων. Στο
Ταυτόχρονα, με αύξηση της διαμέτρου d,
επομένως, μείωση της ταχύτητας V
οι κεφαλαιουχικές δαπάνες θα αυξηθούν και
λειτουργικό κόστος θα
μείωση λόγω μείωσης του υδραυλικού
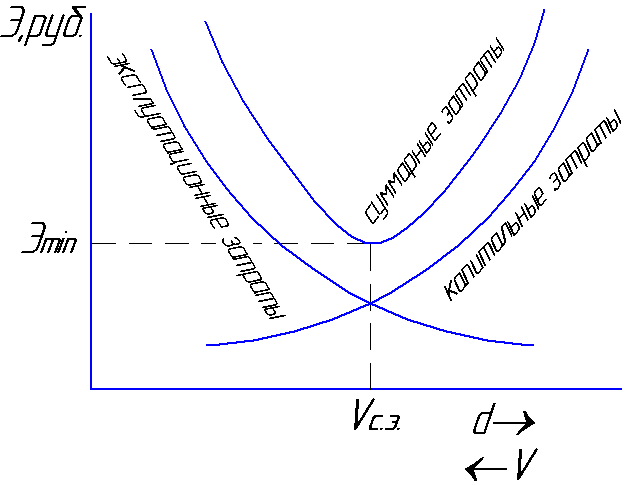
απώλειες. Η ταχύτητα με την οποία το σύνολο
το κόστος θα είναι ελάχιστο
θα ονομαστεί η μέση οικονομική
ταχύτητα Vσ.ε
= 0,8 ... 1,3 m / s (Εικ. 6.1).
εικ.6.1
Τότε
ο τύπος γραμμικής απώλειας (6.1) παίρνει τη μορφή
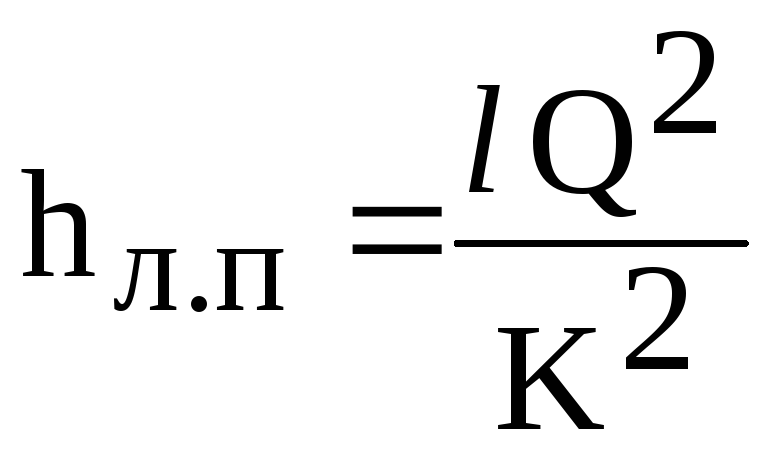
(6.2)
που
K - χαρακτηριστικό ροής του αγωγού
(μέτρο ροής), ανάλογα με το υλικό
αγωγός, διάμετρος και ροή. είναι πιασμένο
από τραπέζια.
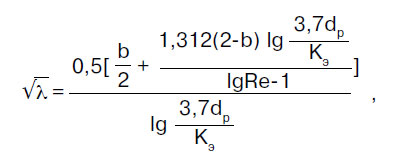
 ),ΝΤΟ
),ΝΤΟ ,
,