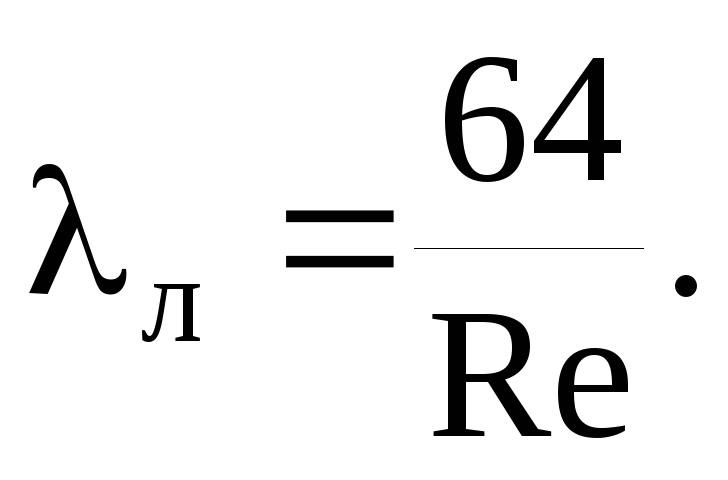1. Hydrostaattinen paine
Hydrostaattinen paine on
aiheuttama sisäinen puristusvoima
kohdistettujen ulkoisten voimien vaikutuksesta
annettu piste nesteessä. Sellainen paine
kaikkiin suuntiin on sama ja riippuu
pisteen sijainnista nesteessä levossa.
Hydrostaattisen paineen mitta
MKGSS-järjestelmässä - kg / cm2 tai t / m2,
SI-järjestelmässä - N/m2.
Perusyksikkösuhteet
paine:
|
kg/cm2 |
N/m2 |
|
|
tekninen tunnelma |
1 |
98066,5 |
|
millimetriä vesipatsaasta |
0,0001 |
9,80665 |
|
elohopeamillimetriä |
0,00136 |
133,32 |
Käytännön laskelmissa 1 tekninen
ilmakehä \u003d 1 kg / cm2 \u003d 10 m vettä. Taide. =
735 mmHg Taide. = 98070 N/m2.
Kokoonpuristumattomalle nesteelle
tasapainossa voiman alla
painovoima, täysi hydrostaattinen
pistepaine:
p=p+

missä p on vapaa paine
nestemäinen pinta;

korkeus h pinta-alalla
poikkileikkaus yhtä suuri;
h - upotussyvyys
pisteitä;

Joillekin nesteille arvot
ratkaisemisessa käytetty ominaispaino
tehtävät on annettu liitteessä (välilehti.
P-3).
Ylipaineen arvo yli
ilmakehän (sa)
kutsutaan manometriseksi tai
ylipaine:

Jos paine vapaalla pinnalla
yhtä suuri kuin ilmakehän, sitten ylimääräinen
paine pm=

Ilmakehän alipaine
määrää kutsutaan tyhjiöksi:
Rwack= sa- R.
Ratkaisu useimpiin ongelmiin tästä
osio liittyy käyttöön
hydrostaattisen perusyhtälön

missä z on koordinaatti tai
pisteen merkki.
1. Yleistä tietoa putkistojen hydraulisesta laskennasta
Laskettaessa
putkistoja harkitaan
tasainen, tasainen paine
minkä tahansa nesteen liikettä
turbulenttinen järjestelmä, pyöreä-sylinterimäinen
putket. Nestettä paineputkissa
on paineen alla ja
niiden poikkileikkaukset ovat täysin
täytetty. Nesteen liikettä pitkin
seurauksena
se, että paine sen alussa on suurempi kuin
lopussa.
Hydraulinen
laskelma tehdään sen määrittämiseksi
putkilinjan halkaisija d
tunnetun kanssa
pituus ohituksen varmistamiseksi
tietty virtausnopeus K
tai perustamisesta
tietyllä halkaisijalla ja vaaditulla pituudella
paine ja nestevirtaus. Putket
riippuen niiden pituudesta ja kuviosta
paikat on jaettu yksinkertaisiin
ja monimutkainen. Yksinkertaisiin putkiin
sisältää putkistot, joita ei ole
oksat pitkin pituutta, vakiolla
sama kulu.
Putket
koostuvat halkaisijaltaan samanlaisista putkista
koko pituudelta tai erilaisten putkien osista
halkaisijat ja pituudet. Viimeinen tapaus
viittaa sarjaliitäntään.
Yksinkertaiset putket
pituudesta riippuen juoni paikallisia
vastukset jaetaan lyhyisiin ja
pitkä. lyhyt
putkistoja
ovat
riittävän lyhyet putkistot,
jossa paikallinen vastus
muodostavat yli 10 % hydrauliikasta
pituuden menetys. Niihin kuuluvat esimerkiksi:
sifoniputket, imu
siipipumppujen putket, sifonit (paine
vesiputket tienpenkereen alla),
rakennusten ja rakenteiden sisällä olevat putkistot
jne.
Pitkä
putkistoja
olla nimeltään
putket ovat suhteellisen suuria
pituudet, joissa pään menetys pituussuunnassa
huomattavasti enemmän kuin paikallisia
tappioita. Paikalliset tappiot ovat
alle 5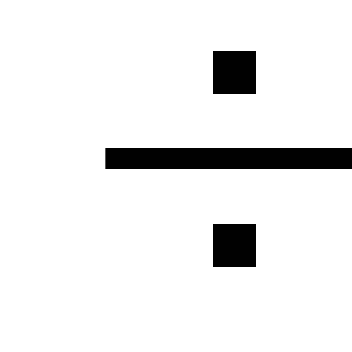
häviöt putkilinjan pituudella ja siksi
ne voidaan jättää huomiotta tai ottaa käyttöön
hydrauliset laskelmat lisääntyvät
kerroin 1,05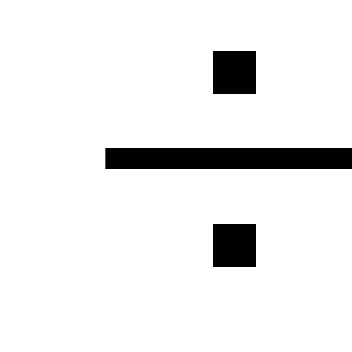
Pitkät putket tulevat järjestelmään
vesijohtoverkot, pumppuputket
asemat, kanavat ja putkistot
teollisuusyritykset ja
maatalouskäyttöön ja
jne.
Monimutkaiset putkistot
niillä on erilaisia oksia pitkin pituutta,
nuo. putkisto koostuu putkiverkostosta
tietyt halkaisijat ja pituudet. Monimutkainen
putkistot on jaettu
yhdensuuntainen, umpikuja (haarautunut),
rengas (suljetut) putkistot,
sisältyy vesihuoltoverkkoon.
Hydraulinen
putkilinjan laskentaa pienennetään
yleensä ratkaisemaan kolme pääongelmaa:
-
määritelmä
putkilinjan virtaus K,
jos tunnettu
paine H,
pituus l
ja halkaisija d
putki,
tiettyjen paikallisten saatavuuden vuoksi
vastukset tai niiden puuttuessa; -
määritelmä
vaadittava paine H,
tarvitaan passin turvaamiseen
tunnettu virtaus K
putken kautta
pitkä l
ja halkaisija d; -
määritelmä
putkilinjan halkaisija d
kun
tunnetut pään arvot H,
kustannuksella K
ja pituus l.
Nesteen virtausnopeus on
missä q > mitoitusvirtaus, m3/s;
- putken jännitteisen osan pinta-ala, m2.
Kitkavastuskerroin λ määritetään säännöstön SP 40-102-2000 "Polymeerimateriaaleista valmistettujen vesihuolto- ja viemärijärjestelmien putkistojen suunnittelu ja asennus" määräysten mukaisesti. Yleiset vaatimukset":
missä b on jokin nestevirtausohjelmien samankaltaisuusluku; kun b > 2, otetaan b = 2.
missä Re on todellinen Reynoldsin luku.
missä ν on nesteen kinemaattisen viskositeetin kerroin, m²/s. Kylmävesiputkia laskettaessa se on 1,31 10-6 m² / s - veden viskositeetti +10 ° C: n lämpötilassa;
Rekv > - Reynoldsin luku, joka vastaa hydraulisen vastuksen neliöalueen alkua.
missä Ke on putkimateriaalin hydraulinen karheus, m. Polymeerimateriaaleista valmistetuille putkille otetaan Ke = 0,00002 m, jos putken valmistaja ei anna muita karheusarvoja.
Niissä virtaustapauksissa, joissa Re ≥ Rekv, parametrin b laskettu arvo tulee yhtä suureksi kuin 2 ja kaava (4) yksinkertaistuu merkittävästi muuttuen tunnetuksi Prandtl-kaavaksi:
Kohdassa Ke = 0,00002 m neliöllinen vastusalue esiintyy veden virtausnopeudella (ν = 1,31 10-6 m²/s) 32,75 m/s, mikä on käytännössä mahdotonta saavuttaa julkisissa vesihuoltojärjestelmissä.
Päivittäisiin laskelmiin suositellaan nomogrammeja ja tarkempia laskelmia varten - "Polymeerimateriaaleista valmistettujen putkistojen hydraulisten laskelmien taulukot", osa 1 "Paineputkistot" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
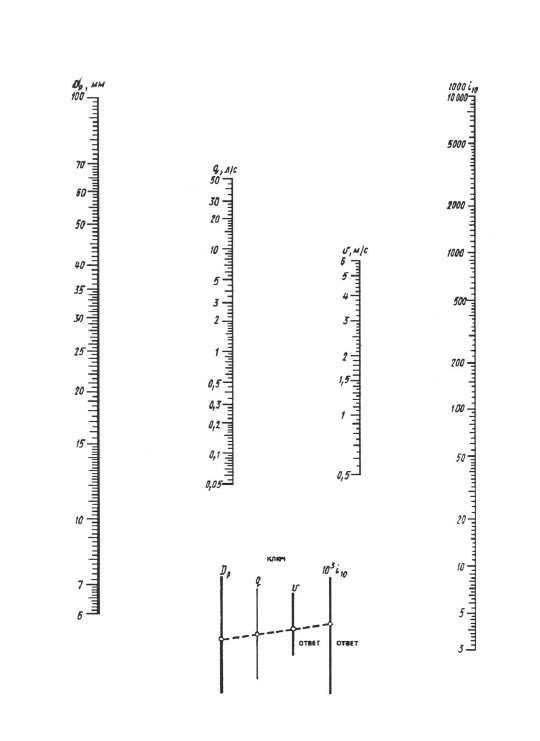
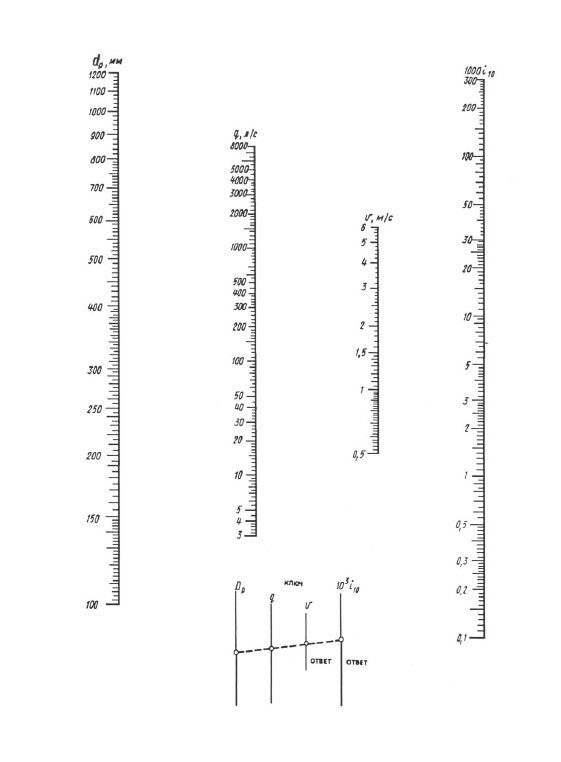
Nomogrammien mukaan laskettaessa tulos saavutetaan yhdellä viivaimen päällekkäisyydellä - sinun tulee yhdistää piste lasketun halkaisijan arvoon dp-asteikolla pisteen lasketun virtausnopeuden arvoon q:ssa (l / s) asteikko suoralla, jatka tätä suoraa, kunnes se leikkaa nopeuden V ja ominaishäviön asteikon 1000 i (mm/m) kanssa. Suoran leikkauspisteet näiden asteikkojen kanssa antavat arvon V ja 1000 i.
Kuten tiedät, nesteen pumppaamiseen tarvittavan sähkön hinta on suoraan verrannollinen H:n arvoon (ceteris paribus). Korvaamalla lausekkeen ( 3 ) kaavaan ( 2 ), on helppo nähdä, että i:n (ja siten H:n) arvo on kääntäen verrannollinen laskettuun halkaisijaan dp viidenteen asteeseen.
Edellä on esitetty, että dp:n arvo riippuu putken seinämän paksuudesta e: mitä ohuempi seinämä, sitä suurempi dp ja vastaavasti pienempi kitkasta johtuva painehäviö ja sähkön hinta.
Jos putken MRS-arvo jostain syystä muuttuu, sen halkaisija ja seinämän paksuus (SDR) on laskettava uudelleen.
On syytä muistaa, että useissa tapauksissa MRS 10 putkien käyttö MRS 8 putkien sijaan, erityisesti putkien MRS 6.3, mahdollistaa putkilinjan halkaisijan pienentämisen yhdellä koolla. Siksi meidän aikanamme polyeteenin PE 80 (MRS 8) ja PE 100 (MRS 10) käyttö polyeteenin PE 63 (MRS 6.3) sijasta putkien valmistukseen mahdollistaa paitsi putkien seinämän paksuuden, myös niiden painon vähentämisen. ja materiaalinkulutusta, mutta myös nesteen pumppauksen energiakustannuksia (ceteris paribus).
Viime vuosina (vuoden 2013 jälkeen) PE80-polyeteenistä valmistetut putket on lähes kokonaan korvattu tuotannosta PE100-polyeteenistä valmistetuilla putkilla. Tämä selittyy sillä, että raaka-aineet, joista putket valmistetaan, toimitetaan ulkomailta PE100-tuotemerkillä.Ja myös se, että polyeteeni 100 -laadulla on enemmän lujuusominaisuuksia, minkä ansiosta putkia valmistetaan samoilla ominaisuuksilla kuin PE80-putkilla, mutta ohuemmalla seinämällä, mikä lisää polyeteeniputkien läpimenoa.
Nomogrammi painehäviöiden määrittämiseen putkissa, joiden halkaisija on 6 100 mm.
Nomogrammi painehäviöiden määrittämiseen putkissa, joiden halkaisija on 100, 1200 mm.
Reynoldsin kriteeri
Tämän riippuvuuden toi esiin englantilainen fyysikko ja insinööri Osborne Reynolds (1842-1912).
Kriteeri, joka auttaa vastaamaan kysymykseen, onko viskositeettia syytä harkita, on Reynoldsin luku Re. Se on yhtä suuri kuin virtaavan nesteen elementin liikeenergian suhde sisäisten kitkavoimien työhön.
Tarkastellaan kuutiometristä nesteelementtiä, jonka reunan pituus on n. Alkuaineen kineettinen energia on:
Newtonin lain mukaan nesteelementtiin vaikuttava kitkavoima määritellään seuraavasti:
Tämän voiman työ siirrettäessä nestettä etäisyyden n yli on
ja neste-elementin kineettisen energian suhde kitkavoiman työhön on
Vähennämme ja saamme:
Re:tä kutsutaan Reynoldsin numeroksi.
Siten Re on dimensioton suure, joka kuvaa viskoosien voimien suhteellista roolia.
Esimerkiksi, jos nesteen tai kaasun kanssa kosketuksissa olevan kappaleen mitat ovat hyvin pienet, niin alhaisellakin viskositeetilla Re on merkityksetön ja kitkavoimat ovat hallitsevassa roolissa. Päinvastoin, jos rungon mitat ja nopeus ovat suuret, niin Re >> 1 ja jopa suuri viskositeetti ei juuri vaikuta liikkeen luonteeseen.
Ei kuitenkaan aina suuret Reynolds-luvut tarkoita, että viskositeetilla ei ole merkitystä. Joten kun Re-luvun erittäin suuri (useita kymmeniä tai satoja tuhansia) arvo saavutetaan, sileä laminaarinen (latinan sanasta lamina - "levy") virtaus muuttuu myrskyiseksi (latinan sanasta turbulentus - "myrskyinen"). , "kaaoottinen"), johon liittyy kaoottisia, epävakaita liikkeitä nesteitä. Tämä vaikutus voidaan havaita, jos avaat vesihanan vähitellen: ohut virta yleensä virtaa tasaisesti, mutta veden nopeuden kasvaessa virtauksen tasaisuus häiriintyy. Korkeassa paineessa ulos virtaavassa suihkussa nestehiukkaset liikkuvat satunnaisesti, värähtelevät, kaikkiin liikkeisiin liittyy voimakas sekoittuminen.
Turbulenssin ilmaantuminen lisää vastusta huomattavasti. Putkilinjassa turbulenttinen virtausnopeus on pienempi kuin laminaarinen virtausnopeus samoilla painehäviöillä. Mutta turbulenssi ei ole aina pahasta. Koska sekoittuminen turbulenssin aikana on erittäin merkittävää, lämmönsiirto - kiviainesten jäähdytys tai lämmitys - tapahtuu paljon voimakkaammin; kemialliset reaktiot leviävät nopeammin.
Bernoullin paikallaan pysyvän liikkeen yhtälö
Sveitsiläinen tiedemies Daniel Bernoulli (1700-1782) sai vuonna 1738 yhden hydromekaniikan tärkeimmistä yhtälöistä. Hän onnistui ensin kuvaamaan ihanteellisen nesteen liikettä Bernoullin kaavalla ilmaistuna.
Ihanteellinen neste on neste, jossa ei ole kitkavoimia ideaalisen nesteen elementtien välillä eikä ideaalinesteen ja astian seinämien välillä.
Hänen nimeään kantava kiinteän liikkeen yhtälö on:
missä P on nesteen paine, ρ on sen tiheys, v on liikkeen nopeus, g on vapaan pudotuksen kiihtyvyys, h on korkeus, jolla nesteen alkuaine sijaitsee.
Bernoullin yhtälön tarkoitus on, että nesteellä täytetyssä järjestelmässä (putkilinjan osa) kunkin pisteen kokonaisenergia on aina muuttumaton.
Bernoullin yhtälössä on kolme termiä:
- ρ⋅v2/2 - dynaaminen paine - kineettinen energia käyttönesteen tilavuusyksikköä kohti;
- ρ⋅g⋅h - painopaine - nestetilavuuden potentiaalienergia;
- P - staattinen paine, sen alkuperä on painevoimien työ, eikä se edusta minkään erityisen energiatyypin reserviä ("paineenergia").
Tämä yhtälö selittää miksi putken kapeissa osissa virtausnopeus kasvaa ja putken seinämiin kohdistuva paine pienenee. Putkien maksimipaine asetetaan juuri siihen kohtaan, jossa putken poikkileikkaus on suurin. Putken kapeat osat ovat tässä suhteessa turvallisia, mutta niiden paine voi pudota niin paljon, että neste kiehuu, mikä voi johtaa kavitaatioon ja putkimateriaalin tuhoutumiseen.
Navier-Stokes-yhtälö viskooseille nesteille
Tiukemmassa muotoilussa viskoosin kitkan lineaarista riippuvuutta nesteen nopeuden muutoksesta kutsutaan Navier-Stokes-yhtälöksi. Se ottaa huomioon nesteiden ja kaasujen kokoonpuristuvuuden, ja toisin kuin Newtonin laki, se pätee paitsi kiinteän kappaleen pinnan lähellä, vaan myös nesteen jokaisessa kohdassa (lähellä kiinteän kappaleen pintaa, jos kyseessä on kokoonpuristumaton kappale). nestettä, Navier-Stokesin yhtälö ja Newtonin laki ovat samat).
Kaikki kaasut, joille jatkuvan väliaineen ehto täyttyy, noudattavat myös Navier-Stokes-yhtälöä, ts. ovat newtonilaisia nesteitä.
Nesteiden ja kaasujen viskositeetti on yleensä merkittävä suhteellisen pienillä nopeuksilla, joten joskus sanotaan, että Euler-hydrodynamiikka on Navier-Stokesin hydrodynamiikan erityinen (rajoittava) tapaus suurille nopeuksille.
Alhaisilla nopeuksilla, Newtonin viskoosin kitkan lain mukaisesti, kappaleen vetovoima on verrannollinen nopeuteen. Suurilla nopeuksilla, kun viskositeetilla ei enää ole merkittävää roolia, rungon vastus on verrannollinen nopeuden neliöön (jonka Newton löysi ja perusti ensimmäisenä).
Hydraulinen laskentajärjestys
1.
Pääkierto valitaan
rengaslämmitysjärjestelmä (useimmat
sijaitsee epäedullisesti hydrauliikassa
suhde). Umpikujassa kaksiputki
järjestelmät on rengas, joka kulkee läpi
alempi instrumentti kauko-ja
ladattu nousuputki, yksiputki -
etäisimmän ja ladatun kautta
nousuputki.
Esimerkiksi,
kaksiputkiisessa lämmitysjärjestelmässä
yläjohdot pääkierto
rengas kulkee lämpöpisteestä
päänousuputken, syöttöjohdon kautta,
kaukaisimman nousuputken kautta, lämmitys
alakerran laite, paluulinja
lämpöpisteeseen.
V
järjestelmät, joihin liittyy veden virtaus sisään
sormus otetaan pääsormuksena,
kulkee eniten keskeltä
ladattu teline.
2.
Pääkiertorengas rikkoutuu
juoniksi (juonta on karakterisoitu
jatkuva veden virtaus ja sama
halkaisija). Kaavio näyttää
osien numerot, niiden pituudet ja lämpö
kuormia. Pääjohdon lämpökuorma
tontit määritetään summaamalla
lämpökuormat, joita nämä palvelevat
juonit. Putken halkaisijan valinta
käytetään kahta määrää:
a)
annettu veden virtaus;
b)
likimääräiset ominaispainehäviöt
kitkaa varten suunnittelukierrossa
rengas Rke.
varten
laskeminen Rcp
täytyy tietää pääosan pituus
kiertorengas ja laskettu
kiertopaine.
3.
Laskettu levikki
kaavan paine
 ,
,
(5.1)
missä
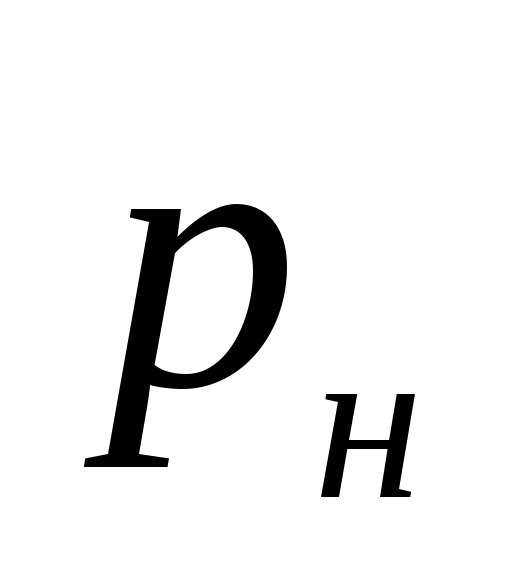
pumpun synnyttämä paine, Pa.
Järjestelmäsuunnittelun käytäntö
lämmitys osoitti sen eniten
on suositeltavaa mitata pumpun paine,
yhtä suuri
 ,
,
(5.2)
missä
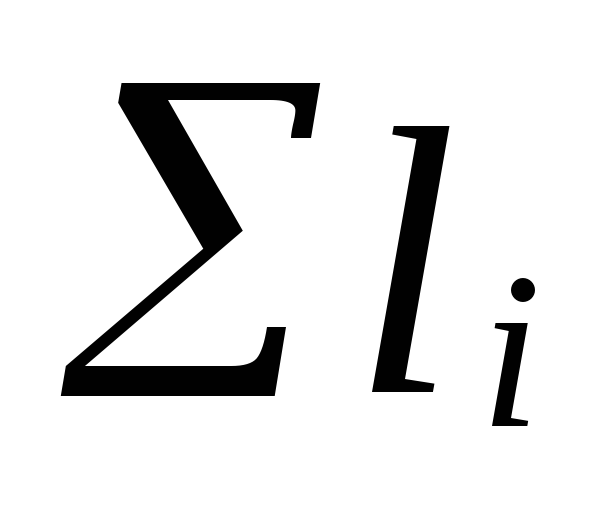
pääkierron osien pituuksien summa
renkaat;
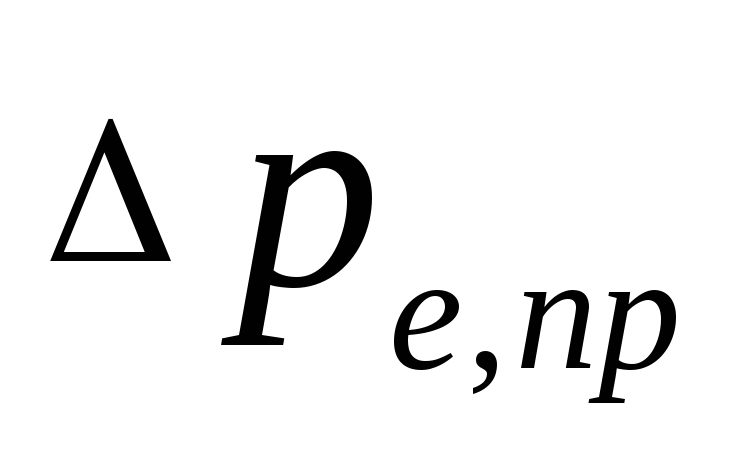
luonnollinen paine, joka syntyy, kun
vesijäähdytys laitteissa, Pa, mahdollista
määrittää kuinka
 ,
,
(5.3)
missä
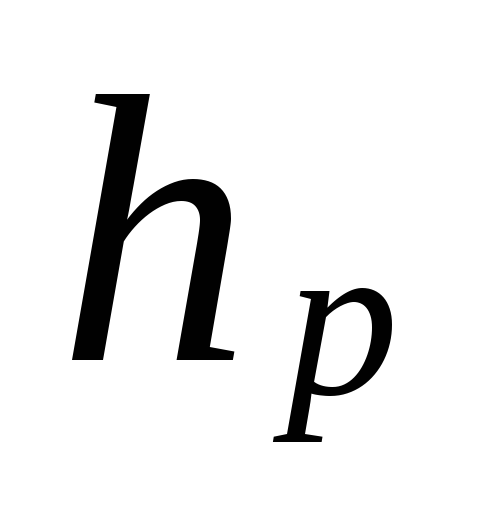
etäisyys pumpun (hissin) keskustasta
alemman kerroksen laitteen keskelle, m.
Merkitys
kerroin mahdollista
määrittää taulukosta 5.1.
pöytä
5.1 - Merkitys c
riippuen suunnittelulämpötilasta
vettä lämmitysjärjestelmässä
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
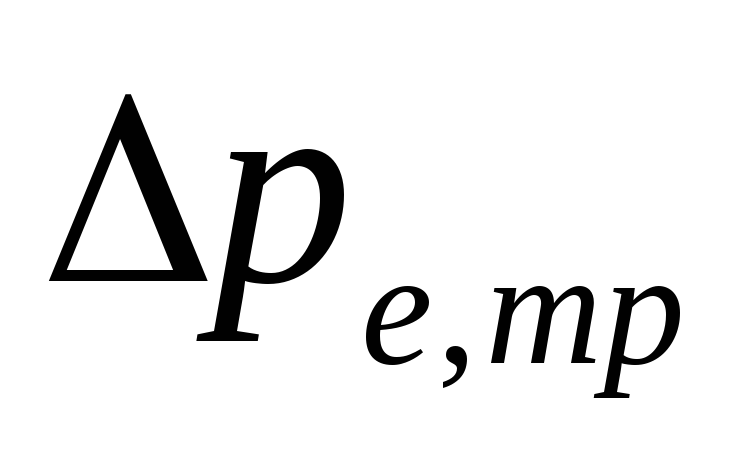
luonnollinen paine sisään
putkistojen vesijäähdytyksen seurauksena
.
V
pumppausjärjestelmät pohjajohdoilla
suuruus
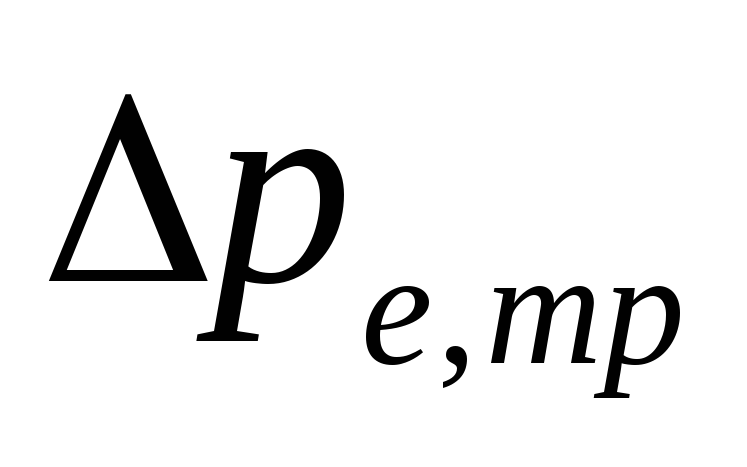
-
ovat määrätietoisia
ominaiskitkapainehäviö
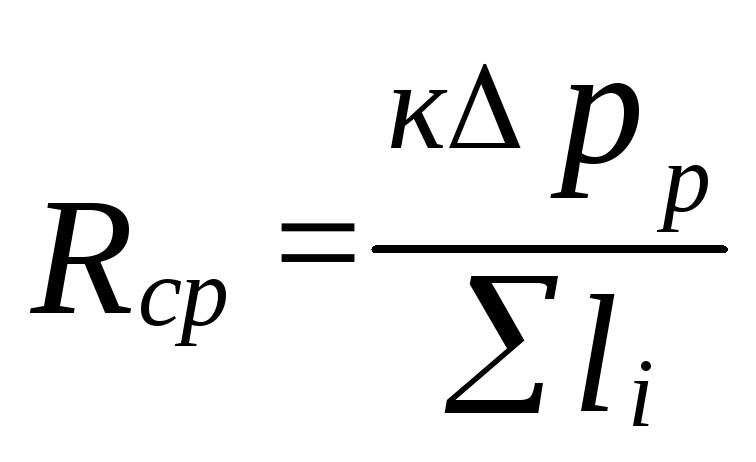
(5.4)
missä
k=0,65 määrittää painehäviöiden osuuden
kitkaa varten.
5.
Alueen veden virtaus määräytyy
kaava
 (5.5)
(5.5)
missä
K
- lämpökuorma työmaalla, W:
(tG
-tO)
- jäähdytysnesteen lämpötilaero.
6.
Suuruuden mukaan
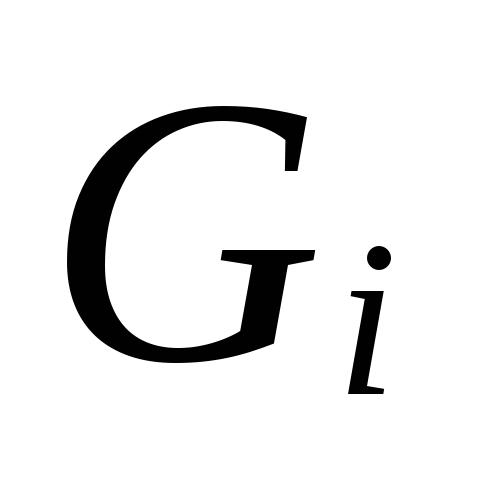
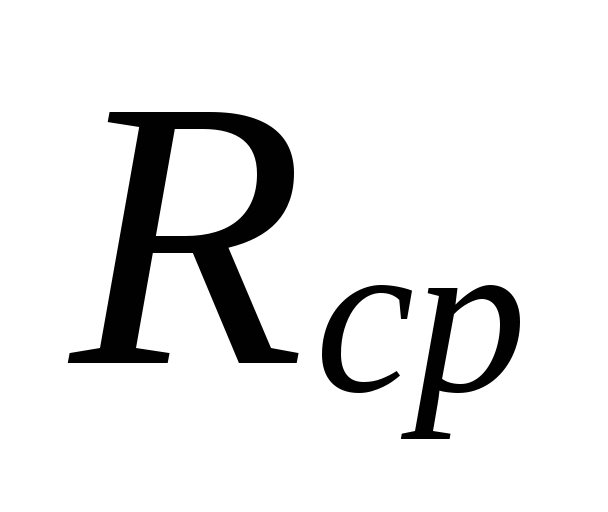
.

6.
Valituille putkistojen halkaisijoille
ja arvioitu vedenkulutus määritetään
jäähdytysnesteen nopeus v
ja todellinen spesifinen
kitkapaineen menetys Rf.
klo
halkaisijoiden valinta pienillä alueilla
jäähdytysnesteen virtausnopeudet voivat olla
välillä suuria eroja
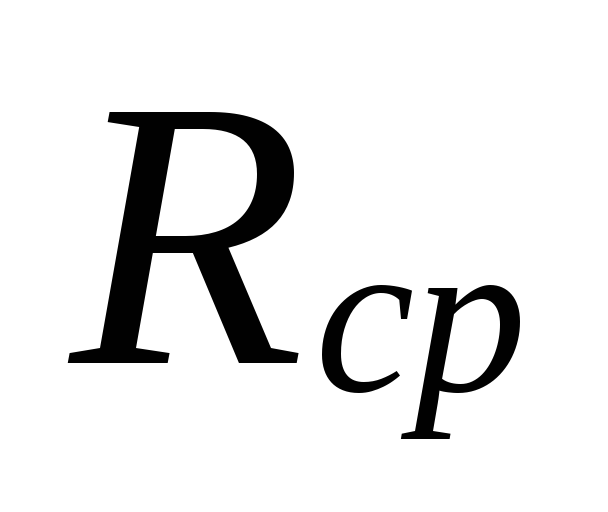
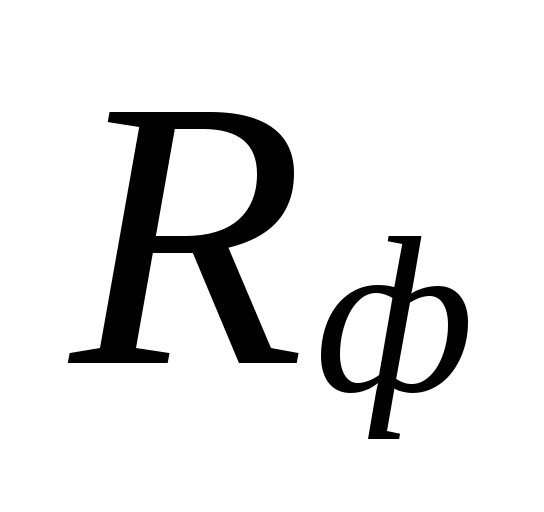
aliarvioituja tappioita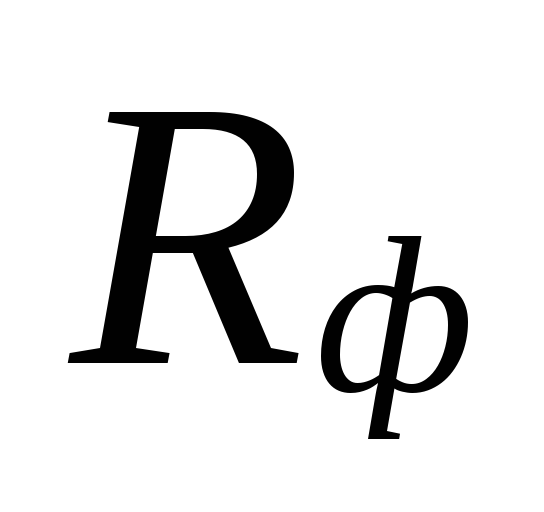
nämä alueet kompensoidaan yliarvioinnilla
määriä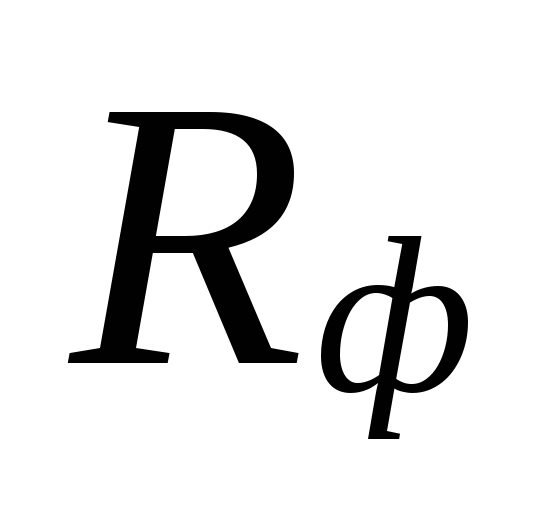
7.
Kitkapainehäviöt määritetään
laskennallisella alueella, Pa:
 .
.
(5.6)
tuloksia
laskelmat on merkitty taulukkoon 5.2.
8.
Painehäviöt paikallisesti
vastukset jommallakummalla kaavalla:
 ,
,
(5.7)
missä
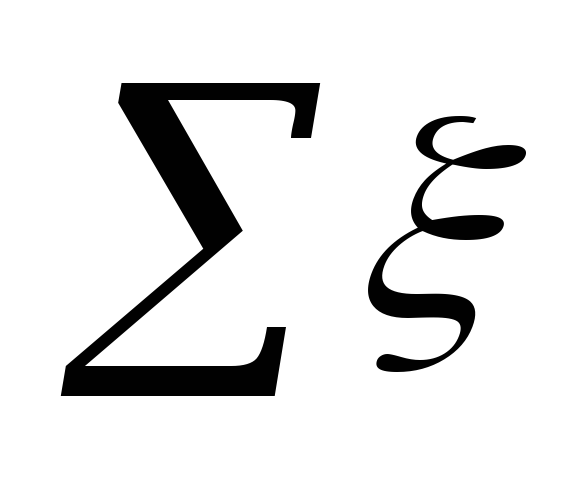
asutusalueella.
Merkitys ξ
kussakin paikassa on yhteenveto taulukossa. 5.3.
Taulukko 5.3 -
Paikalliset vastuskertoimet
|
Nro p / s |
Nimet |
Arvot |
Huomautuksia |
9.
Määritä kokonaispainehäviö
joka alueella
 .
.
(5.8)
10. Määrittele
kitkan aiheuttama kokonaispainehäviö ja
pääasiassa paikallisissa vastuksissa
kiertorengas
 .
.
(5.9)
11. Vertaa Δр
Kanssa ΔрR.
Kokonaispainehäviö renkaassa
on oltava pienempi kuin ΔрR
päällä
 .
.
(5.10)
varasto kertakäyttöisiä
tarvitaan paineita tunnistamattomiin sisään
hydraulisen vastuksen laskeminen.
Jos olosuhteet eivät ole
suoritetaan, se on tarpeen joissakin
renkaan osia putkien halkaisijoiden muuttamiseksi.
12. Laskennan jälkeen
pääkiertorengas
yhdistä loput renkaat. V
vain jokainen uusi rengas laskee
muita ei-yhteisiä tiloja,
kytketty rinnan osien kanssa
päärengas.
Häviön ristiriita
paineet rinnakkaisliitännässä
tontteja sallitaan jopa 15 % umpikujalla
veden liike ja jopa 5% - ohituksen kanssa.
pöytä
5.2 - Hydraulisen laskennan tulokset
lämmitysjärjestelmää varten
|
Käytössä |
Tekijä: |
Tekijä: |
||||||||||||||
|
Määrä |
Lämpö |
Kulutus |
Pituus |
Halkaisija |
Nopeus |
Erityinen |
Tappiot |
Summa |
Tappiot |
d, |
v, |
R, |
Δрtr, |
∑ξ |
Z, |
Rl+Z, |
Oppitunti 6
Kaasun lämpötilan muutos kaasuputken pituudella
Kiinteässä kaasuvirtauksessa massa
virtausnopeus kaasuputkessa on
 . (2.41)
. (2.41)
Itse asiassa kaasun liike kaasuputkessa
on aina ei-isoterminen. V
Puristuksen aikana kaasu lämpenee.
Jopa sen jäähtymisen jälkeen COP:ssa lämpötila
kaasua tulee putkilinjaan
on noin 2040С,
joka on paljon korkeampi kuin lämpötila
ympäristö (T).
Käytännössä kaasun lämpötila muuttuu
lähellä ympäristön lämpötilaa
vain halkaisijaltaan pienille kaasuputkille
(Dy0.
Lisäksi se on otettava huomioon
putkitettu kaasu
on todellinen kaasu, mikä on luontaista
Joule-Thompson-ilmiö, joka ottaa huomioon
lämmön imeytyminen kaasun laajenemisen aikana.
Kun lämpötila muuttuu pituussuunnassa
kaasuputken kaasuliikettä kuvataan
yhtälöjärjestelmä:
spesifistä energiaa ,
,
jatkuvuus ,
,
toteaa ,
,
lämpötasapaino .
.
Tarkastellaan yhtälöä ensimmäisessä approksimaatiossa
lämpötasapainoa ottamatta huomioon vaikutusta
Joule Thompson. Yhtälön integrointi
lämpötasapaino
 ,
,
saamme
 , (2.42)
, (2.42)
missä ;
;
KSR- sivuston keskimääräinen täynnä
lämmönsiirtokerroin kaasusta toiseen
ympäristö;
G on kaasun massavirtausnopeus;
cP–
kaasun keskimääräinen isobarinen lämpökapasiteetti.
arvotL:tä kutsutaan dimensiottomaksi kriteeriksi
Shukhov
 (2.43)
(2.43)
Eli kaasun lämpötila lopussa
kaasuputki tulee olemaan
 . (2.44)
. (2.44)
Etäisyydellä x alusta
kaasuputken kaasun lämpötila määritetään
kaavan mukaan
 . (2.45)
. (2.45)
Lämpötilan muutos kaasuputken pituudella
on eksponentiaalinen (kuva.
2.6).
Harkitse
kaasun lämpötilan muutoksen vaikutus
putkilinjan suorituskyky.
Kerrotaan tietyn yhtälön molemmat puolet
energia on 2 ja ilmaisee ,
,
saamme
 . (2.46)
. (2.46)
Ilmaisemme kaasun tiheyden vasemmalla puolella
lausekkeet (2.46) tilayhtälöstä
 ,
,
tuotew jatkuvuusyhtälöstä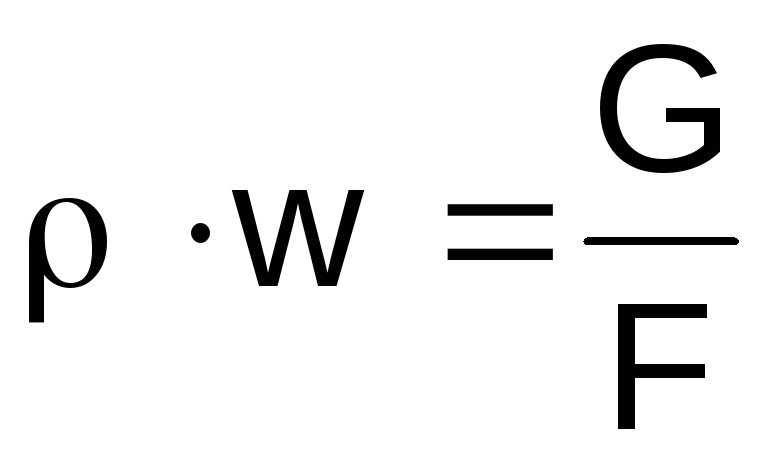
saldo .
.
Tämä huomioon ottaen erityinen yhtälö
energia saa muodon
 (2.47)
(2.47)
tai
 . (2.48)
. (2.48)
Merkitsee
 ja integroimalla yhtälön vasen puoli
ja integroimalla yhtälön vasen puoli
(2.48) PHdoPTO, ja oikealle kohdasta THpisteTO, saamme
 . (2.49)
. (2.49)
Vaihtamalla
 , (2.50)
, (2.50)
meillä on
 . (2.51)
. (2.51)
Integroinnin jälkeen ilmoitettuun
rajat, saamme

 . (2.52)
. (2.52)
Ottaen huomioon (2.42)

tai
 , (2.53)
, (2.53)
missä on korjauskerroin, joka ottaa huomioon
on korjauskerroin, joka ottaa huomioon
lämpötilan muutos kaasuputken pituudella
(kaasuvirran ei-isotermisyys).
Ottaen huomioon (2.53) riippuvuus määrityksessä
kaasun massavirtaus saa muodon
 . (2.54)
. (2.54)
Arvo Haina suurempi kuin yksi, joten
kaasun massavirtaus vaihtaessaan
lämpötila kaasuputken pituudella
(ei-isoterminen virtausjärjestelmä) aina
vähemmän kuin isotermisessä tilassa
(T = idem). Tuote THkutsutaan keskiarvointegraaliksi
kaasun lämpötila putkilinjassa.
Shukhov-luvun Shu4 arvoilla
kaasun virtaus putkessa
pitää lähes isotermisenä
osoitteessa T=idem. Sellainen lämpötila
tila on mahdollista pumpattaessa kaasua
alhaiset kaasuputkikustannukset
pienestä (alle 500 mm) halkaisijaltaan merkittävään
etäisyys.
Kaasun lämpötilan muutoksen vaikutus
ilmenee Shukhov-luvun arvoille
Shu
klo
kaasun pumppaus kaasuläpän läsnäolosta
vaikutus johtaa syvemmälle
kaasujäähdytys kuin vain lämmönvaihdolla
maaperän kanssa. Tässä tapauksessa lämpötila
kaasu voi jopa pudota alle
lämpötila T (kuva.
2.7).
Riisi. 2.7. Joule-Thompson-ilmiön vaikutus
kaasun lämpötilan jakautumisesta
putkilinjan pituus
1 - ottamatta huomioon Di; 2 - kanssa
ottaen huomioon Di
Sitten ottaen huomioon Joule-Thompson-kerroin
lämpötilan muutoksen laki pituudella
ottaa muodon
 , (2.55)
, (2.55)
5 Hydrauliset häviöt
Ero
öljynpaine kahdessa osassa
ja sama putki, edellyttäen että
ensimmäinen sijaitsee ylävirtaan, ja
toinen - alla, määritetään yhtälö
Bernoulli
 ,
,
missä
h2
– h1
- painopisteiden korkeusero
osia mielivaltaisesti valitusta
vaakatasossa;
v1,
v2
– öljyn keskimääräiset nopeudet osissa;
g - voiman kiihtyvyys
painovoima;

hydrauliset häviöt liikkeen aikana
öljyt ensimmäisestä osasta toiseen.
Yhtälö
Bernoulli täydessä käytössä
pumppujen imulinjojen laskemiseen;
muissa tapauksissa ensimmäinen termi,
yleensä laiminlyödään ja harkitaan:

hydraulinen
tappiot jaetaan yleensä paikallisiin
häviöt ja kitkahäviöt pitkin pituutta
putket (lineaariset).
1.5.1
paikalliset tappiot
energiat johtuvat paikallisista
hydraulinen vastus,
aiheuttaa virtauksen vääristymiä. Paikallinen
vastukset ovat: supistukset,
putkistojen laajentaminen, pyöristäminen,
suodattimet, ohjauslaitteet ja
säätö jne. Virtattaessa
nesteitä paikallisten vastusten kautta
sen nopeus muuttuu ja yleensä on
suuria pyörteitä.
Tappiot
paikallisten vastusten aiheuttamaa painetta
määräytyy kaavan mukaan Weisbach:
 MPa
MPa
(tai
 isä),
isä),
missä

tappio,
v
on keskimääräinen virtausnopeus poikkileikkauksen yli
putkessa paikallisvastuksen takana, m/s;
,
N/m3;
g = 9,81 m/s2.
Jokainen
on ominaista paikallinen vastustuskyky
kertoimen arvolla

Pyörteisellä virtauksella arvot
vastustuskykyä ja muutosta hyvin vähän
osuuden koon, nopeuden muutoksella
nesteen virtaus ja viskositeetti. Niin
oletetaan, että ne eivät riipu numerosta
Reynolds Re.
Arvot

esimerkiksi t-paidoissa, joissa on sama
kanavan halkaisijat ovat yhtä suuret,
jos:
purot
laskea yhteen, erota; virtaus
ohittaminen;









klo
putken mutka

Arvot

laitteiden hydraulijärjestelmissä, otettu
viitekirjallisuutta.
klo
laminaarivirtaus (Re
Tappiot
paikallisten vastusten aiheuttama paine klo
laminaarivirtaus määräytyy
kaava:
 MPa
MPa
missä

= a

Määrät
painehäviö vakiona
hydrauliset laitteet
yleensä nimellinen virtausnopeus
lueteltu niiden teknisissä tiedoissa.
1.5.2
Tappio päälle
pituus kitka
on energiahäviö, joka tapahtuu
suorissa putkissa, joiden poikkileikkaus on vakio,
nuo. tasaisella nestevirtauksella,
ja kasvaa suhteessa pituuteen
putket. Nämä tappiot johtuvat sisäisistä
kitkaa nesteessä, ja siksi niillä on
aseta sekä karkeisiin että sileisiin putkiin.
Tappiot
putkilinjan kitkapaine
määräytyy kaavan mukaan Darcy:
 MPa
MPa
missä

l
ja d
- putkilinjan pituus ja sisähalkaisija,
mm.
Tämä
kaava soveltuu sekä laminaarisille,
samoin kuin pyörteisessä virtauksessa; ero
koostuu vain kertoimen arvoista

klo
laminaarivirtaus (Re
klo
turbulenttisen virtauksen kitkakerroin
ei ole vain Re:n funktio, vaan
riippuu myös sisäpuolen karheudesta
putken pinta. varten hydraulisesti
sileä putket,
nuo. sellaisella karkeudella
ei käytännössä vaikuta sen vastustuskykyyn,
turbulenttinen kitkakerroin
tila voidaan määrittää kaavalla PC.
Konakova:

putki
katsotaan hydraulisesti sileäksi, jos
(d/k)>(Re/20),
missä k on ekvivalentti karheus,
mm. Esimerkiksi uudelle saumattomalle teräkselle
putket k≈0,03
mm, ja useiden vuosien käytön jälkeen
k≈0,2
mm, uusille saumattomille putkille
ei-rautametallit k≈0,005
mm. Näitä putkia käytetään usein
työstökoneiden hydraulijärjestelmät.
Kerroin
turbulenttisessa järjestelmässä voi olla kitkaa
määrittää kaavalla Altshulya,
on universaali (eli sovellettavissa
Joka tapauksessa):

2. Putkilinjan virtausmoduulin virtausominaisuudet
Muistetaan
lineaarinen häviökaava - Darcy-kaava
- Weisbach:
 .
.
Ilmaista
tässä kaavassa nopeus V
virtauksen Q läpi
suhteesta
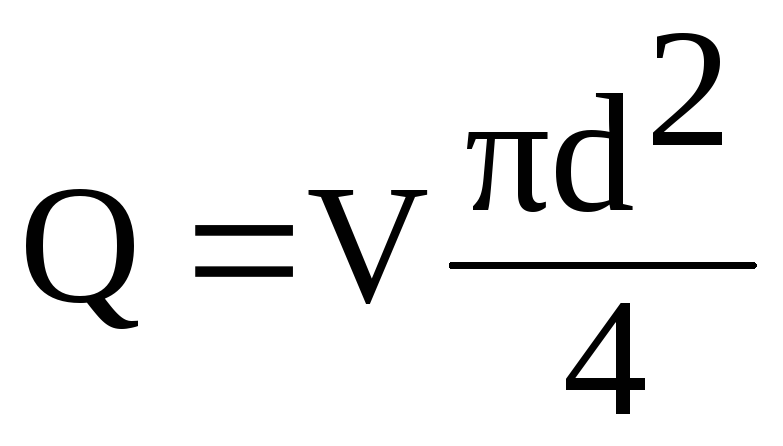
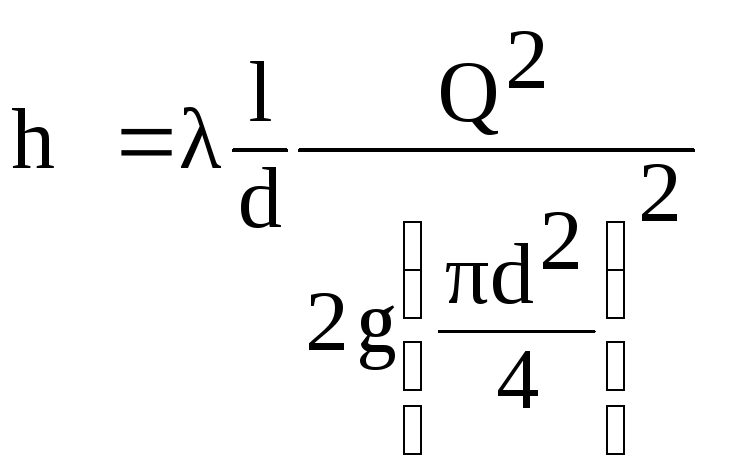
(6.1)
varten
tietyn halkaisijan omaava putki
määrien kompleksi
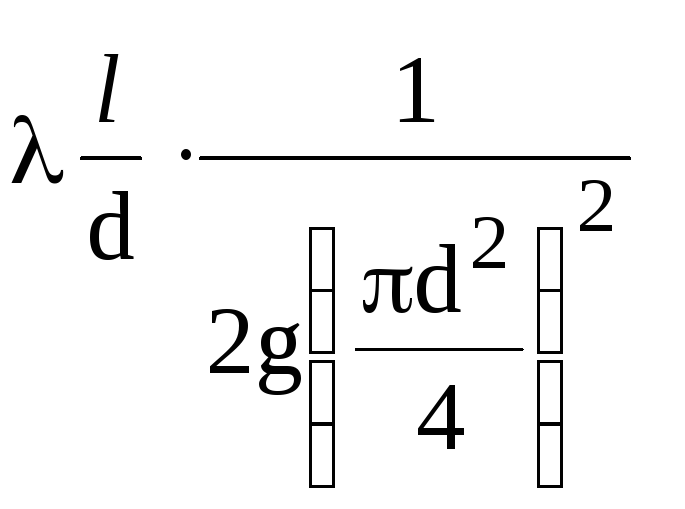
vakio (1/K2),
paitsi hydraulinen kerroin
kitka λ. Perustuu konseptiin
Keskimääräinen taloudellinen nopeus Vs.e
osoitetaan, että ilmoitettu kerroin λ
voidaan johtua tästä kompleksista, koska v
Tässä tapauksessa Reynoldsin luku on
niillä on erityinen merkitys:
 ,
,
ja Nikuradze-kuvaajalla kerroin λ in
tässä tapauksessa on erityinen
merkitys.
Perustella
käsitteen käyttöönoton legitiimiys
keskimääräinen taloudellinen nopeus seuraavasti
perustelut.
hydraulinen
järjestelmä, kuten putkisto,
voit ohittaa tietyn kulun
valmistettu halkaisijaltaan eri putkista. klo
Samaan aikaan, kun halkaisija d kasvaa,
siksi nopeuden V lasku
pääomamenot nousevat ja
käyttökustannukset tulevat
lasku hydrauliikan heikkenemisen vuoksi
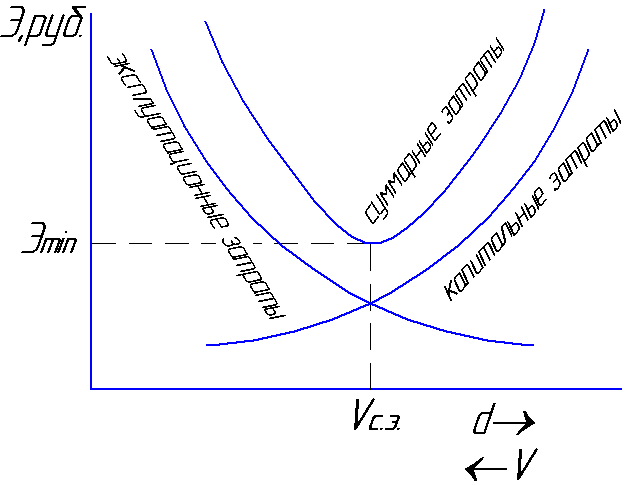
tappioita. Nopeus, jolla yhteensä
kustannukset jäävät minimaalisiksi
kutsutaan keskimääräiseksi taloudeksi
nopeus Vs.e
= 0,8 ... 1,3 m / s (kuva 6.1).
kuva 6.1
Sitten
lineaarihäviön kaava (6.1) saa muodon
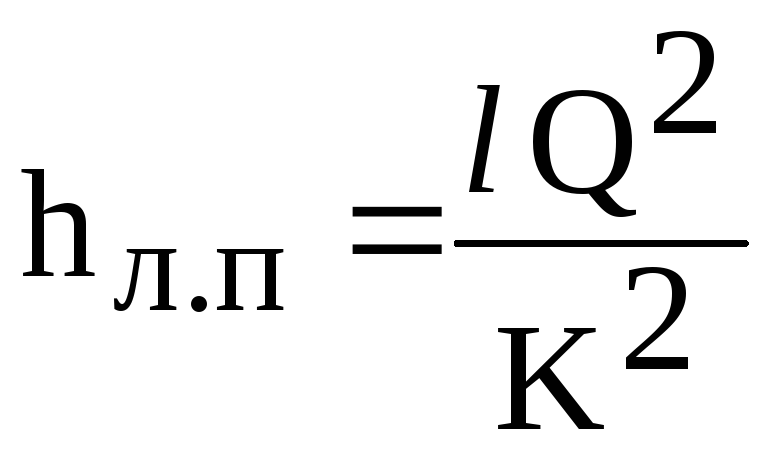
(6.2)
missä
K - putkilinjan virtausominaisuus
(virtausmoduuli), materiaalista riippuen
putki, halkaisija ja virtaus. on otettu
pöydistä.
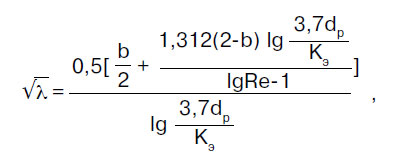
 ),C
),C ,
,