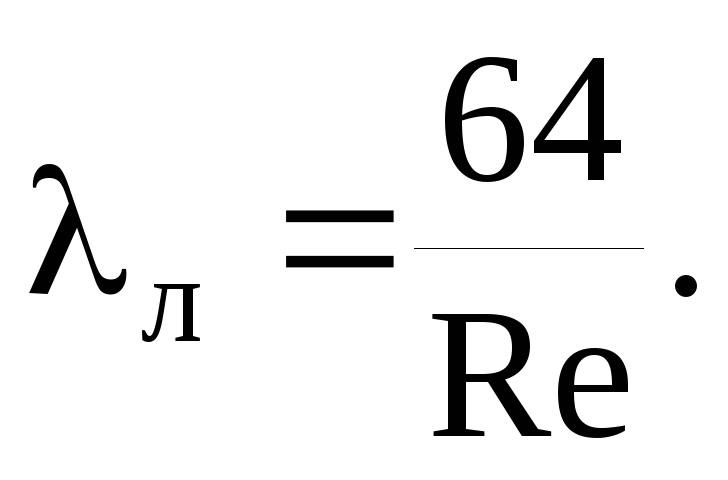1. Hidrostatinis slėgis
Hidrostatinis slėgis yra
vidinė gniuždymo jėga dėl
veikiant išorinėms jėgoms
duotame taške skystyje. Toks spaudimas
visomis kryptimis yra vienodas ir priklauso
apie taško padėtį skystyje ramybės būsenoje.
Hidrostatinio slėgio matmenys
MKGSS sistemoje - kg / cm2 arba t / m2,
SI sistemoje - N/m2.
Pagrindiniai vienetų santykiai
slėgis:
|
kg/cm2 |
N/m2 |
|
|
techninė atmosfera |
1 |
98066,5 |
|
milimetras vandens stulpelio |
0,0001 |
9,80665 |
|
gyvsidabrio milimetro |
0,00136 |
133,32 |
Praktiniuose skaičiavimuose 1 techninis
atmosfera \u003d 1 kg / cm2 \u003d 10 m vandens. Art. =
735 mmHg Art. = 98070 N/m2.
Nesuspaudžiamam skysčiui, kuris yra
pusiausvyra veikiant jėgai
gravitacija, pilna hidrostatinė
taško slėgis:
p=p+

kur p yra slėgis laisvai
skysčio paviršius;

aukštis h su plotu
skerspjūvis lygus vienetui;
h - panardinimo gylis
taškų;

Kai kurių skysčių vertės
sprendžiant naudojamas savitasis svoris
užduotys pateiktos priede (tab.
P-3).
Perteklinio slėgio vertė virš
atmosferos (pa)
vadinamas manometriniu arba
perteklinis slėgis:

Jei spaudimas ant laisvo paviršiaus
lygus atmosferiniam, tada perteklius
spaudimas pm=

Žemas atmosferos slėgis
kiekis vadinamas vakuumu:
Rbjaurus= pa– R.
Daugumos šios problemos sprendimas
skyrius yra susijęs su naudojimu
pagrindinė hidrostatikos lygtis

kur z yra koordinatė arba
taško ženklas.
1. Bendra informacija apie vamzdynų hidraulinį skaičiavimą
Skaičiuojant
svarstomi vamzdynai
pastovus, vienodas slėgis
bet kokio skysčio judėjimas
turbulentinis režimas, apvalios cilindrinės formos
vamzdžiai. Skystis slėgio vamzdžiuose
patiria spaudimą ir
jų skerspjūviai yra visiškai
užpildytas. Skysčio judėjimas kartu
dujotiekis atsiranda dėl to
tai, kad slėgis jo pradžioje yra didesnis nei
pabaigoje.
Hidraulinis
apskaičiavimas atliekamas siekiant nustatyti
dujotiekio skersmuo d
su žinomu
ilgis, kad būtų užtikrintas praleidimas
tam tikras srautas K
arba nustatant
esant tam tikram skersmeniui ir reikiamam ilgiui
slėgis ir skysčio srautas. Vamzdynai
priklausomai nuo jų ilgio ir rašto
vietos skirstomos į paprastas
ir sudėtingas. Prie paprastų vamzdynų
apima vamzdynus, kurių nėra
šakos išilgai, su konstanta
tos pačios išlaidos.
Vamzdynai
susideda iš to paties skersmens vamzdžių
per visą ilgį arba iš skirtingų vamzdžių sekcijų
skersmenys ir ilgiai. Paskutinis atvejis
nurodo nuoseklųjį ryšį.
Paprasti vamzdynai
priklausomai nuo ilgio su sklypu vietos
varžos skirstomos į trumpąsias ir
ilgas. trumpas
vamzdynai
yra
pakankamai trumpo ilgio vamzdynai,
kuriame vietinis pasipriešinimas
sudaro daugiau nei 10% hidraulinių
ilgio praradimas. Pavyzdžiui, jie apima:
sifoniniai vamzdžiai, siurbimas
mentinių siurblių vamzdžiai, sifonai (slėgis
vandens vamzdžiai po kelio pylimu),
vamzdynai pastatų ir konstrukcijų viduje
ir tt
ilgas
vamzdynai
paskambino
vamzdynai yra gana dideli
ilgiai, kuriuose galvos praradimas išilgai ilgio
gerokai lenkia vietines
nuostoliai. Vietiniai nuostoliai yra
mažiau nei 5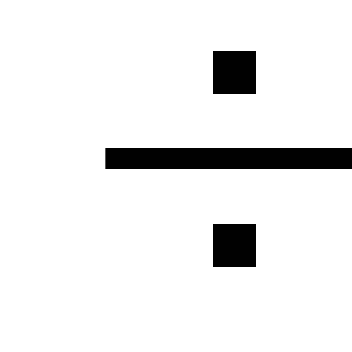
nuostoliai per dujotiekio ilgį, todėl
jų galima nepaisyti arba įvesti
hidrauliniai skaičiavimai didėja
koeficientas lygus 1,05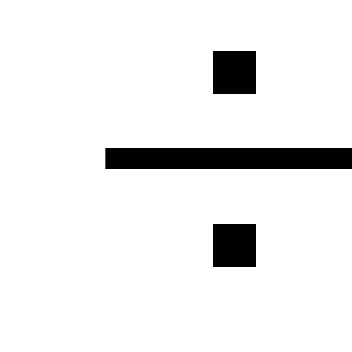
Į sistemą patenka ilgi vamzdynai
vandentiekio tinklai, siurblinės vamzdynai
stotys, vamzdynai ir vamzdynai
pramonės įmonės ir
žemės ūkio paskirties ir
ir tt
Sudėtingi vamzdynai
turėti skirtingas šakas išilgai,
tie. vamzdynas susideda iš vamzdžių tinklo
tam tikri skersmenys ir ilgiai. Sudėtingas
vamzdynai skirstomi į
lygiagretus, aklavietė (šakota),
žiediniai (uždaryti) vamzdynai,
įtrauktas į vandentiekio tinklą.
Hidraulinis
dujotiekio skaičiavimas sumažinamas kaip
paprastai išsprendžia tris pagrindines problemas:
-
apibrėžimas
dujotiekio srautas K,
jei žinoma
spaudimas H,
ilgio l
ir skersmuo d
vamzdynas,
atsižvelgiant į tam tikrų vietinių
pasipriešinimas arba jų nebuvimas; -
apibrėžimas
reikalingas slėgis H,
būtinas leidimui užtikrinti
žinomas srautas K
vamzdynu
ilgas l
ir skersmuo d; -
apibrėžimas
dujotiekio skersmuo d
kada
žinomos galvos vertės H,
išlaidas K
ir ilgis l.
Skysčio srauto greitis yra
čia q > projektinis skysčio srautas, m3/s;
- vamzdžio įtemptos dalies plotas, m2.
Atsparumo trinčiai koeficientas λ nustatomas vadovaujantis taisyklių rinkinio SP 40-102-2000 „Vandentiekio ir kanalizacijos vamzdynų iš polimerinių medžiagų projektavimas ir montavimas“ nuostatomis. Bendrieji reikalavimai":
čia b yra tam tikras skysčio srauto režimų panašumo skaičius; b > 2 imama b = 2.
kur Re yra tikrasis Reinoldso skaičius.
čia ν – skysčio kinematinės klampos koeficientas, m²/s. Skaičiuojant šalto vandens vamzdžius, jis yra lygus 1,31 10-6 m² / s - vandens klampumas +10 ° C temperatūroje;
Rekv > – Reinoldso skaičius, atitinkantis hidraulinio pasipriešinimo kvadratinės srities pradžią.
čia Ke – vamzdžio medžiagos hidraulinis šiurkštumas, m. Vamzdžiams iš polimerinių medžiagų imamas Ke = 0,00002 m, jei vamzdžio gamintojas nenurodo kitų šiurkštumo verčių.
Tais srauto atvejais, kai Re ≥ Rekv, apskaičiuotoji parametro b reikšmė tampa lygi 2, o formulė (4) žymiai supaprastėja, virsta gerai žinoma Prandtl formule:
Esant Ke = 0,00002 m, kvadratinio pasipriešinimo sritis susidaro, kai vandens debitas (ν = 1,31 10-6 m²/s) lygus 32,75 m/s, o tai praktiškai nepasiekiama viešose vandens tiekimo sistemose.
Kasdieniams skaičiavimams rekomenduojamos nomogramos, o tikslesniams skaičiavimams – „Vamzdynų iš polimerinių medžiagų hidraulinių skaičiavimų lentelės“, 1 tomas „Slėgio vamzdynai“ (A.Ya. Dobromyslov, M., VNIIMP, 2004).
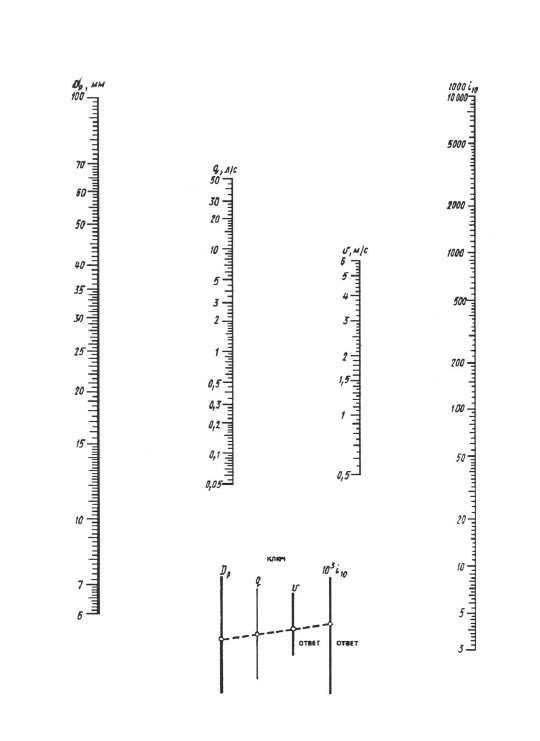
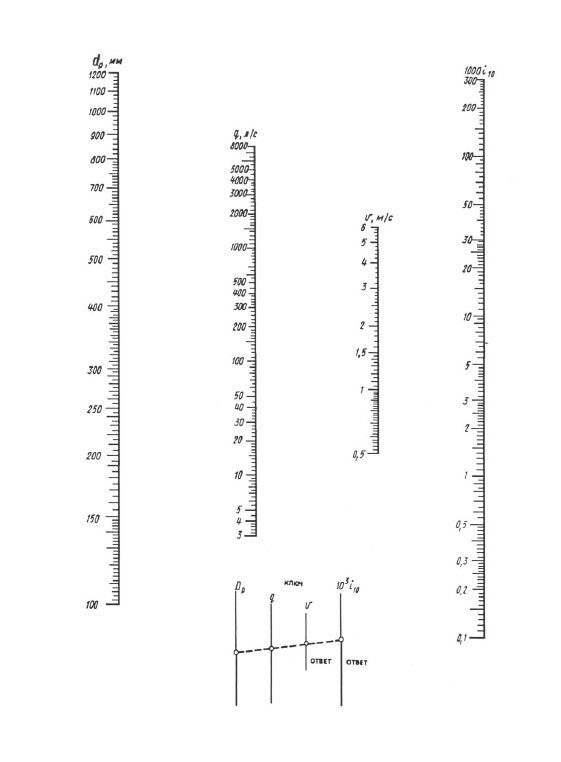
Skaičiuojant pagal nomogramas, rezultatas pasiekiamas naudojant vieną liniuotės perdangą - tašką su apskaičiuoto skersmens reikšme dp skalėje turėtumėte sujungti su tašku su apskaičiuoto srauto dydžiu q (l / s) mastelį tiesia linija, tęskite šią tiesę, kol susikirs su greičio V skalėmis ir savitųjų nuostolių 1000 i (mm/m) skalėmis. Tiesios susikirtimo taškai su šiomis mastelėmis duoda reikšmę V ir 1000 i.
Kaip žinote, elektros energijos kaina skysčiui siurbti yra tiesiogiai proporcinga H vertei (ceteris paribus). Pakeitus išraišką ( 3 ) į formulę ( 2 ), nesunku pastebėti, kad i reikšmė (ir atitinkamai H) yra atvirkščiai proporcinga apskaičiuotam skersmeniui dp iki penkto laipsnio.
Aukščiau parodyta, kad dp reikšmė priklauso nuo vamzdžio sienelės storio e: kuo plonesnė sienelė, tuo didesnis dp ir atitinkamai mažesni slėgio nuostoliai dėl trinties ir elektros sąnaudos.
Jei dėl kokių nors priežasčių pasikeičia vamzdžio MRS reikšmė, reikia perskaičiuoti jo skersmenį ir sienelės storį (SDR).
Reikėtų nepamiršti, kad daugeliu atvejų vamzdžių su MRS 10 naudojimas vietoj vamzdžių su MRS 8, ypač vamzdžių su MRS 6.3, leidžia sumažinti vamzdyno skersmenį vienu dydžiu. Todėl mūsų laikais vamzdžių gamybai vietoj polietileno PE 63 (MRS 6.3) panaudojimas polietileno PE 80 (MRS 8) ir PE 100 (MRS 10) leidžia ne tik sumažinti vamzdžių sienelių storį, jų svorį. ir medžiagų sąnaudas, bet ir sumažinti energijos sąnaudas skysčiui siurbti (ceteris paribus).
Pastaraisiais metais (po 2013 m.) PE80 polietileno vamzdžiai iš gamybos beveik visiškai pakeisti vamzdžiais iš PE100 klasės polietileno. Tai paaiškinama tuo, kad žaliavos, iš kurių gaminami vamzdžiai, tiekiamos iš užsienio su PE100 prekės ženklu.Taip pat dėl to, kad polietilenas 100 klasė turi daugiau stiprumo charakteristikų, dėl kurių vamzdžiai gaminami tokiomis pačiomis charakteristikomis kaip ir vamzdžiai iš PE80, tačiau su plonesne sienele, taip padidinant polietileno vamzdynų pralaidumą.
Nomograma, skirta nustatyti slėgio nuostolius vamzdžiuose, kurių skersmuo 6 100 mm.
Nomograma, skirta slėgio nuostoliams nustatyti vamzdžiuose, kurių skersmuo 100, 1200 mm.
Reinoldso kriterijus
Šią priklausomybę iškėlė anglų fizikas ir inžinierius Osborne'as Reinoldsas (1842-1912).
Kriterijus, padedantis atsakyti į klausimą, ar reikia atsižvelgti į klampumą, yra Reinoldso skaičius Re. Jis lygus tekančio skysčio elemento judėjimo energijos ir vidinių trinties jėgų darbo santykiui.
Apsvarstykite kubinį skysčio elementą, kurio krašto ilgis n. Elemento kinetinė energija yra:
Pagal Niutono dėsnį skysčio elementą veikianti trinties jėga apibrėžiama taip:
Šios jėgos darbas judant skysčio elementui atstumu n yra
o skysčio elemento kinetinės energijos ir trinties jėgos darbo santykis yra
Sumažiname ir gauname:
Re vadinamas Reinoldso skaičiumi.
Taigi Re yra bematis dydis, apibūdinantis santykinį klampių jėgų vaidmenį.
Pavyzdžiui, jei kūno, su kuriuo liečiasi skystis ar dujos, matmenys yra labai maži, tada net ir esant mažam klampumui Re bus nereikšmingas, o trinties jėgos vaidins vyraujantį vaidmenį. Priešingai, jei kūno matmenys ir greitis yra dideli, tai Re >> 1 ir net didelis klampumas beveik neturės įtakos judesio pobūdžiui.
Tačiau ne visada dideli Reynoldso skaičiai reiškia, kad klampumas nevaidina jokio vaidmens. Taigi, pasiekus labai didelę (kelias dešimtis ar šimtus tūkstančių) Re skaičiaus reikšmę, lygus laminarinis (iš lot. lamina - „plokštė“) srautas virsta audringu (iš lot. turbulentus - „audringa“). , „chaotiškas“), lydimas chaotiškų, nepastovių judesių skysčių. Tokį efektą galima pastebėti pamažu atidarius vandens čiaupą: plona srovelė dažniausiai teka tolygiai, tačiau didėjant vandens greičiui, tėkmės lygumas sutrinka. Aukštu slėgiu ištekančioje srovėje skysčio dalelės juda atsitiktinai, svyruoja, visą judėjimą lydi stiprus maišymasis.
Turbulencijos atsiradimas labai padidina pasipriešinimą. Dujotiekyje turbulentinis srauto greitis yra mažesnis nei laminarinis srauto greitis esant tokiems pat slėgio kritimams. Tačiau neramumai ne visada yra blogai. Dėl to, kad maišymasis turbulencijos metu yra labai reikšmingas, šilumos perdavimas – agregatų vėsinimas ar kaitinimas – vyksta daug intensyviau; cheminės reakcijos plinta greičiau.
Bernulio nejudančio judėjimo lygtis
Vieną iš svarbiausių hidromechanikos lygčių 1738 metais gavo šveicarų mokslininkas Danielis Bernoulli (1700-1782). Pirmiausia jam pavyko apibūdinti idealaus skysčio judėjimą, išreikštą Bernulio formule.
Idealus skystis yra skystis, kuriame nėra trinties jėgų tarp idealaus skysčio elementų, taip pat tarp idealaus skysčio ir indo sienelių.
Stacionaraus judėjimo lygtis, pavadinta jo vardu:
čia P – skysčio slėgis, ρ – jo tankis, v – judėjimo greitis, g – laisvojo kritimo pagreitis, h – aukštis, kuriame yra skysčio elementas.
Bernulio lygties reikšmė yra ta, kad sistemoje, užpildytoje skysčiu (dujotiekio atkarpa), kiekvieno taško bendra energija visada nekinta.
Bernulio lygtis turi tris terminus:
- ρ⋅v2/2 - dinaminis slėgis - varančiojo skysčio tūrio vieneto kinetinė energija;
- ρ⋅g⋅h - svorio slėgis - skysčio tūrio vieneto potenciali energija;
- P - statinis slėgis, savo kilme yra slėgio jėgų darbas ir neatspindi jokios specialios energijos rūšies ("slėgio energijos") rezervo.
Ši lygtis paaiškina, kodėl siaurose vamzdžio atkarpose srauto greitis didėja, o slėgis ant vamzdžio sienelių mažėja. Didžiausias slėgis vamzdžiuose nustatomas tiksliai toje vietoje, kur vamzdis turi didžiausią skerspjūvį. Siauros vamzdžio dalys šiuo atžvilgiu yra saugios, tačiau slėgis jose gali nukristi tiek, kad skystis užvirs, o tai gali sukelti kavitaciją ir vamzdžio medžiagos sunaikinimą.
Klampių skysčių Navier-Stokes lygtis
Griežtesnėje formulėje klampios trinties tiesinė priklausomybė nuo skysčio greičio pokyčio vadinama Navier-Stokes lygtimi. Jame atsižvelgiama į skysčių ir dujų suspaudžiamumą ir, skirtingai nei Niutono dėsnis, galioja ne tik prie kieto kūno paviršiaus, bet ir kiekviename skysčio taške (netoli kieto kūno paviršiaus, jei jis nesuspaudžiamas). skystis, Navier-Stokes lygtis ir Niutono dėsnis sutampa).
Bet kokios dujos, kurioms tenkinama nuolatinės terpės sąlyga, taip pat paklūsta Navier-Stokes lygčiai, t.y. yra Niutono skysčiai.
Skysčių ir dujų klampumas dažniausiai yra reikšmingas esant santykinai mažiems greičiams, todėl kartais teigiama, kad Eilerio hidrodinamika yra ypatingas (ribinis) Navier-Stokes hidrodinamikos didelių greičių atvejis.
Esant mažam greičiui, pagal Niutono klampios trinties dėsnį, kūno pasipriešinimo jėga yra proporcinga greičiui. Esant dideliam greičiui, kai klampumas nustoja vaidinti reikšmingą vaidmenį, kūno pasipriešinimas yra proporcingas greičio kvadratui (kurį pirmasis atrado ir pagrindė Niutonas).
Hidraulinio skaičiavimo seka
1.
Parenkamas pagrindinis tiražas
žiedinė šildymo sistema (dauguma
nepalankiai išdėstytas hidraulinėje sistemoje
santykis). Dviejų vamzdžių aklavietėje
sistemos yra žiedas, einantis pro juos
apatinis instrumentas labiausiai nutolęs ir
pakrautas stovas, vienvamzdis -
per labiausiai nutolusias ir įkeltas
stovas.
Pavyzdžiui,
dviejų vamzdžių šildymo sistemoje su
viršutinė laidų pagrindinė cirkuliacija
žiedas praeis iš šilumos punkto
per pagrindinį stovą, tiekimo liniją,
per labiausiai nutolusį stovą, šildymą
apatinio aukšto prietaisas, grįžtama linija
į šilumos punktą.
V
sistemos su susijusiu vandens judėjimu
žiedas imamas kaip pagrindinis,
eina per vidurį labiausiai
pakrautas stovas.
2.
Pagrindinis cirkuliacinis žiedas nutrūksta
į sklypus (siužetas charakterizuojamas
nuolatinis vandens srautas ir tas pats
skersmuo). Diagrama rodo
sekcijų numeriai, jų ilgiai ir terminis
apkrovų. Pagrindinės šiluminė apkrova
sklypai nustatomi sumuojant
šiluminės apkrovos, kurias aptarnauja šie
sklypai. Norėdami pasirinkti vamzdžio skersmenį
naudojami du kiekiai:
a)
nustatytas vandens srautas;
b)
apytiksliai specifiniai slėgio nuostoliai
dėl trinties projektavimo apyvartoje
žiedas Rtrečia.
Dėl
skaičiavimas Rcp
reikia žinoti pagrindinio ilgio
cirkuliacinis žiedas ir apskaičiuojamas
cirkuliacinis slėgis.
3.
Apskaičiuotas tiražas
formulės slėgis
 ,
,
(5.1)
kur
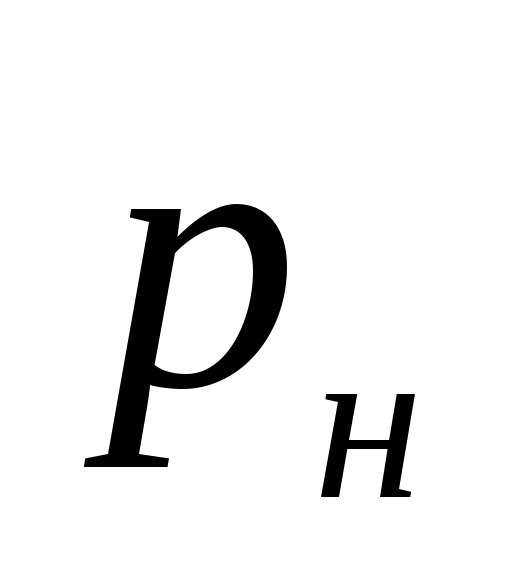
siurblio sukurtas slėgis, Pa.
Sistemos projektavimo praktika
šildymas parodė, kad labiausiai
patartina išmatuoti siurblio slėgį,
lygus
 ,
,
(5.2)
kur
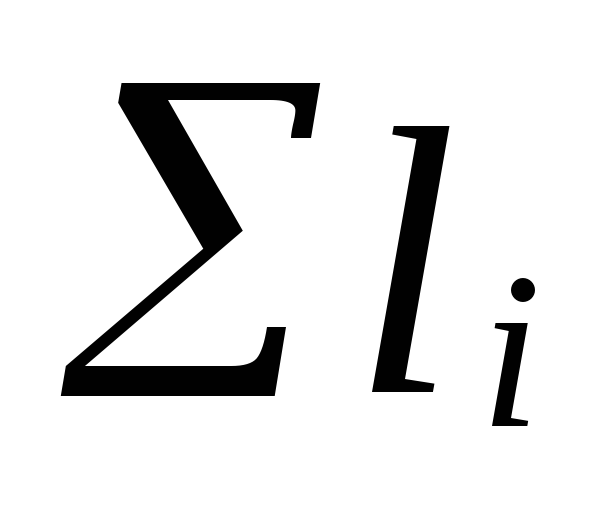
pagrindinio tiražo sekcijų ilgių suma
žiedai;
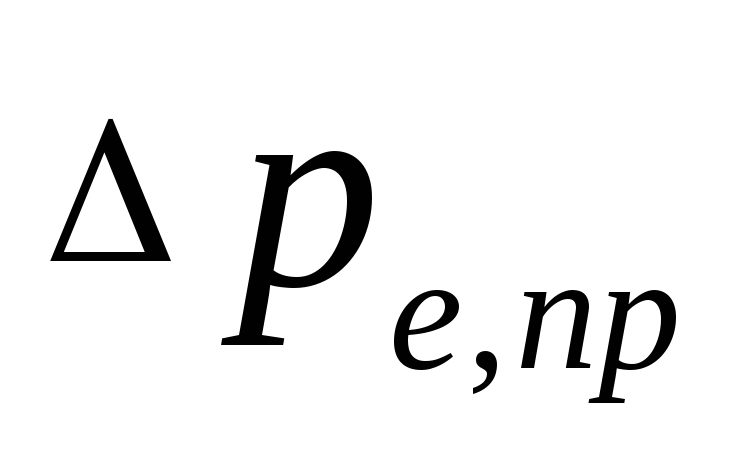
natūralus spaudimas, atsirandantis, kai
aušinimas vandeniu buitiniuose prietaisuose, Pa, galimas
nustatyti kaip
 ,
,
(5.3)
kur
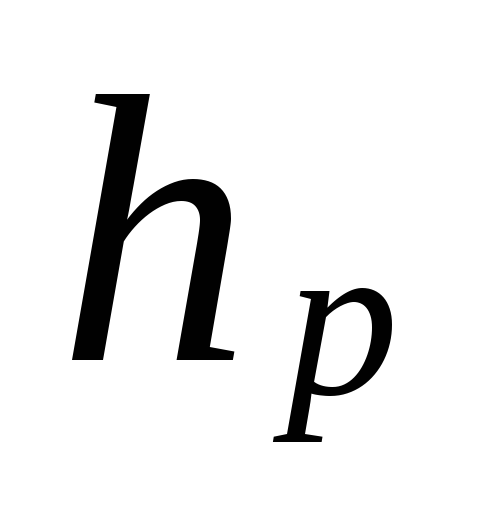
atstumas nuo siurblio (lifto) centro
iki apatinio aukšto įrenginio centro, m.
Reikšmė
koeficientas įmanoma
nustatyti pagal 5.1 lentelę.
stalo
5.1 – prasmė c
priklausomai nuo projektinės temperatūros
vanduo šildymo sistemoje
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
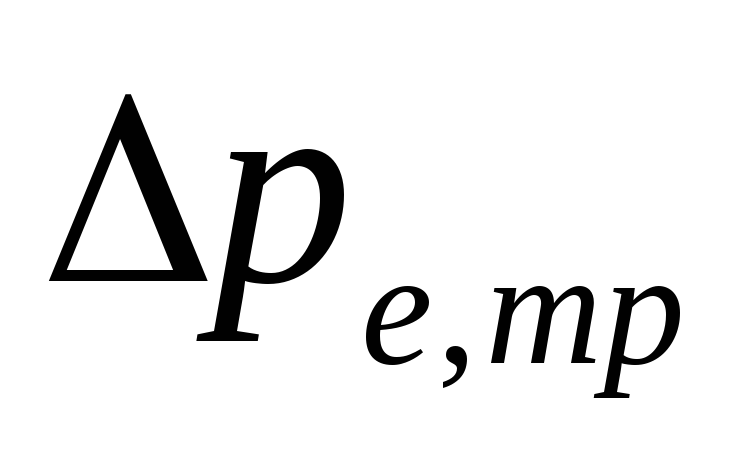
natūralus slėgis
dėl vandens aušinimo vamzdynuose
.
V
siurbimo sistemos su apatine instaliacija
dydžio
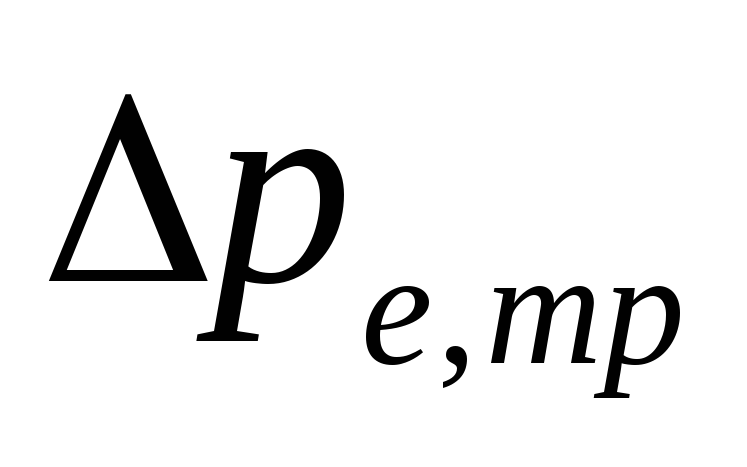
-
Yra pasiryžę
specifinis trinties slėgio nuostolis
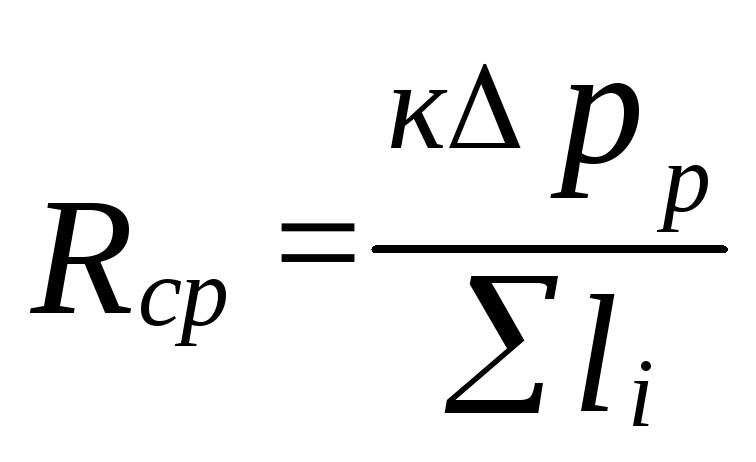
(5.4)
kur
k=0,65 lemia slėgio nuostolių proporciją
dėl trinties.
5.
Vandens srautą rajone lemia
formulę
 (5.5)
(5.5)
kur
K
- šilumos apkrova aikštelėje, W:
(tG
– tO)
- aušinimo skysčio temperatūros skirtumas.
6.
Pagal dydį
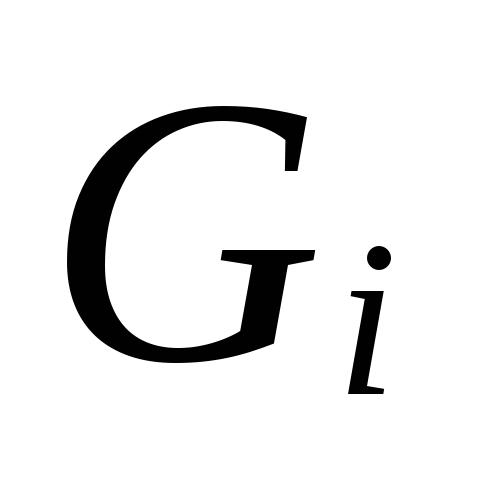
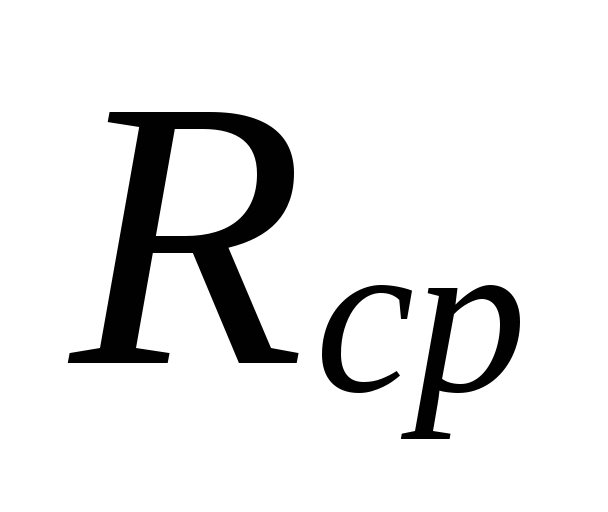
.

6.
Pasirinktiems vamzdynų skersmenims
ir nustatomas numatomas vandens suvartojimas
aušinimo skysčio greitis v
ir tikrasis specifinis
trinties slėgio praradimas Rf.
At
skersmenų pasirinkimas mažose srityse
aušinimo skysčio srautai gali būti
dideli neatitikimai tarp
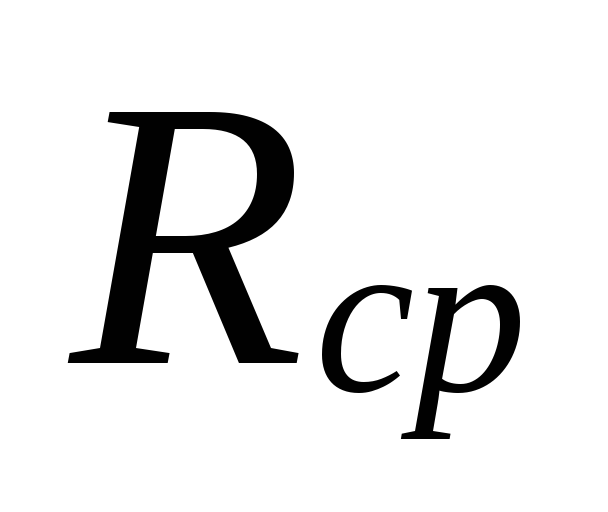
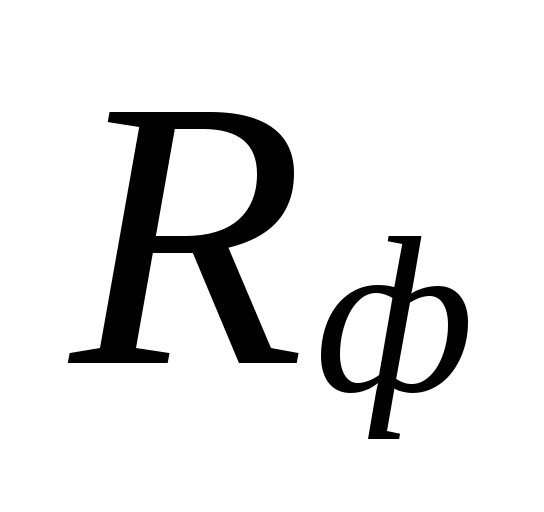
neįvertintų nuostolių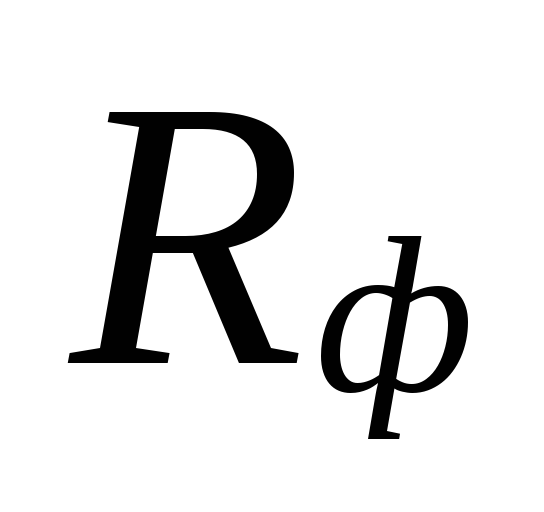
šios sritys kompensuojamos pervertinimu
kiekiai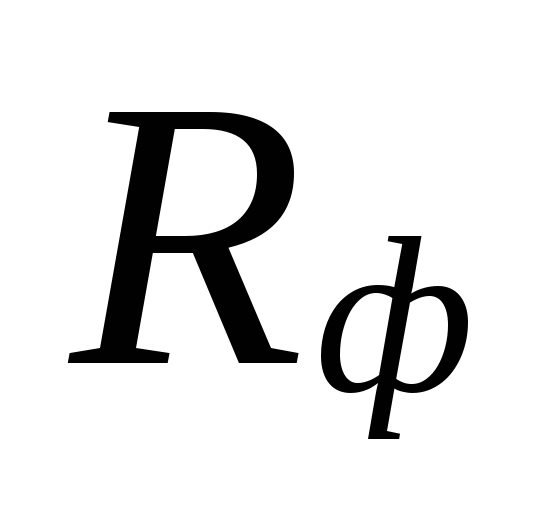
7.
Nustatomi trinties slėgio nuostoliai
pagal skaičiuojamąjį plotą, Pa:
 .
.
(5.6)
rezultatus
skaičiavimai įrašyti į 5.2 lentelę.
8.
Slėgio nuostoliai vietiniuose
pasipriešinimas naudojant bet kurią formulę:
 ,
,
(5.7)
kur
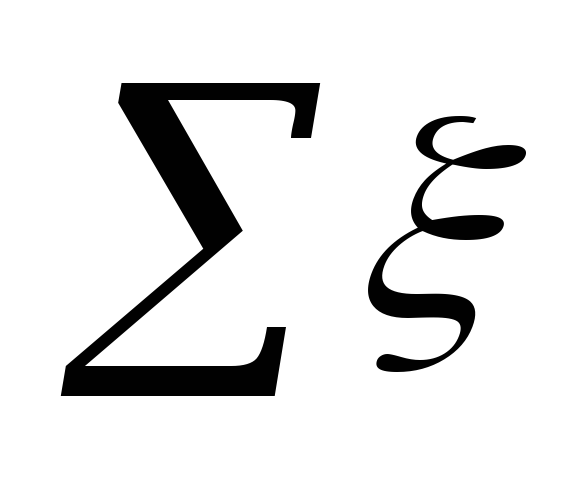
gyvenvietėje.
Reikšmė ξ
kiekvienoje svetainėje yra apibendrinti lentelėje. 5.3.
5.3 lentelė -
Vietos varžos koeficientai
|
Nr. p / p |
Vardai |
Vertybės |
Pastabos |
9.
Nustatykite bendrą slėgio nuostolį
kiekvienoje srityje
 .
.
(5.8)
10. Nustatykite
bendras slėgio nuostolis dėl trinties ir
vietiniuose pasipriešinimuose pagrinde
cirkuliacinis žiedas
 .
.
(5.9)
11. Palyginkite Δp
Su ΔpR.
Bendras slėgio praradimas žiede
turi būti mažesnis nei ΔpR
ant
 .
.
(5.10)
vienkartinių atsargų
reikalingas spaudimas neapskaitytoms vietoms
hidraulinio pasipriešinimo skaičiavimas.
Jei sąlygų nėra
atliekami, kai kuriems tai būtina
žiedo sekcijos, kad pakeistumėte vamzdžių skersmenis.
12. Po skaičiavimo
pagrindinis cirkuliacinis žiedas
sujunkite likusius žiedus. V
skaičiuojamas tik kiekvienas naujas žiedas
papildomos ne bendro naudojimo patalpos,
sujungti lygiagrečiai su sekcijomis
pagrindinis žiedas.
Nuostolių neatitikimas
lygiagrečiai prijungtas slėgis
sklypai leidžiami iki 15% su aklaviete
vandens judėjimas ir iki 5% - su praėjimu.
stalo
5.2 - Hidraulinio skaičiavimo rezultatai
šildymo sistemai
|
Ant |
Autorius |
Autorius |
||||||||||||||
|
Skaičius |
terminis |
Vartojimas |
Ilgis |
Skersmuo |
Greitis |
Specifinis |
Nuostoliai |
Suma |
Nuostoliai |
d, |
v, |
R, |
Δptr, |
∑ξ |
Z, |
Rl+Z, |
6 pamoka
Dujų temperatūros pokytis per dujotiekio ilgį
Stacionariame dujų sraute masė
debitas dujotiekyje yra
 . (2.41)
. (2.41)
Tiesą sakant, dujų judėjimas dujotiekyje
visada yra neizoterminis. V
Suspaudimo metu dujos įkaista.
Net po jo aušinimo COP, temperatūra
dujos patenka į dujotiekį
yra apie 2040С,
kuri yra daug aukštesnė už temperatūrą
aplinka (T).
Praktiškai dujų temperatūra tampa
artima aplinkos temperatūrai
tik mažo skersmens dujotiekiams
(Dy0.
Be to, reikia atsižvelgti į tai
dujotiekio dujos
yra tikros dujos, kurios yra būdingos
Joule-Thompson efektas, kuriame atsižvelgiama į
šilumos sugėrimas dujų plėtimosi metu.
Kai temperatūra keičiasi išilgai
aprašytas dujotiekio dujų judėjimas
lygčių sistema:
specifinė energija ,
,
tęstinumą ,
,
teigia ,
,
šilumos balansas .
.
Pirmajame aproksime apsvarstykite lygtį
šilumos balansas neatsižvelgiant į poveikį
Joule'as Thompsonas. Lygties integravimas
šilumos balansas
 ,
,
mes gauname
 , (2.42)
, (2.42)
kur ;
;
KSR- vidutiniškai pilna svetainėje
šilumos perdavimo koeficientas iš dujų į
aplinka;
G – dujų masės srautas;
cP–
vidutinė izobarinė dujų šiluminė talpa.
vertybėtL vadinamas bedimensiniu kriterijumi
Šuchovas
 (2.43)
(2.43)
Taigi dujų temperatūra pabaigoje
bus dujotiekis
 . (2.44)
. (2.44)
X atstumu nuo pradžios
dujotiekio dujų temperatūra nustatoma
pagal formulę
 . (2.45)
. (2.45)
Temperatūros pokytis per dujotiekio ilgį
yra eksponentinis (pav.
2.6).
Apsvarstykite
dujų temperatūros pokyčio įtaka
dujotiekio veikimas.
Padauginus abi konkrečios lygties puses
energijos ant 2 ir išreiškiant ,
,
mes gauname
 . (2.46)
. (2.46)
Kairėje pusėje išreiškiame dujų tankį
išraiškos (2.46) iš būsenos lygties
 ,
,
sandaugawiš tęstinumo lygties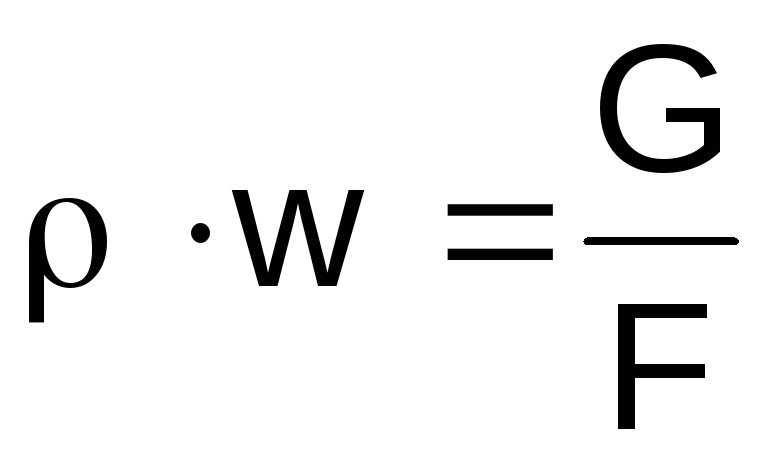
pusiausvyrą .
.
Turint tai omenyje, specifinė lygtis
energija įgauna formą
 (2.47)
(2.47)
arba
 . (2.48)
. (2.48)
Žymintys
 ir integruojant kairę lygties pusę
ir integruojant kairę lygties pusę
(2,48) iš PHdoPKAMir į dešinę nuo THdoTKAM, mes gauname
 . (2.49)
. (2.49)
Keičiant
 , (2.50)
, (2.50)
mes turime
 . (2.51)
. (2.51)
Integravus į nurodytą
ribas, mes gauname

 . (2.52)
. (2.52)
Atsižvelgiant į (2.42)

arba
 , (2.53)
, (2.53)
kur yra pataisos koeficientas, į kurį atsižvelgiama
yra pataisos koeficientas, į kurį atsižvelgiama
temperatūros pokytis per dujotiekio ilgį
(dujų srauto neizotermiškumas).
Atsižvelgiant į (2.53), priklausomybę nustatant
dujų masės srautas įgaus formą
 . (2.54)
. (2.54)
Vertė Hvisada didesnis už vieną, taigi
dujų masės srautą keičiant
temperatūra per dujotiekio ilgį
(neizoterminio srauto režimas) visada
mažiau nei izoterminiu režimu
(T=idem). Prekė THvadinamas vidutiniu integralu
dujų temperatūra vamzdyne.
Su Shukhov skaičiaus Shu4 reikšmėmis
dujų srautas vamzdyne
laikyti beveik izoterminiu
ties T=idem. Tokia temperatūra
režimas galimas siurbiant dujas su
mažos dujotiekio sąnaudos
mažo (mažiau nei 500 mm) skersmens iki reikšmingo
atstumas.
Dujų temperatūros pasikeitimo poveikis
pasireiškia Šukovo skaičiaus reikšmėmis
Šu
At
dujų siurbimas, kai yra droselis
poveikis veda į gilesnį
aušinimas dujomis nei tik su šilumos mainais
su žeme. Šiuo atveju temperatūra
dujos gali net nukristi žemiau
temperatūra T (pav.
2.7).
Ryžiai. 2.7. Joule-Thompson efekto įtaka
apie dujų temperatūros pasiskirstymą
dujotiekio ilgis
1 - neatsižvelgiant į Di; 2 - su
atsižvelgiant į Di
Tada, atsižvelgiant į Joule-Thompson koeficientą
temperatūros kitimo išilgai dėsnis
įgauna formą
 , (2.55)
, (2.55)
5 Hidrauliniai nuostoliai
Skirtumas
alyvos slėgis dviejose vienos sekcijose
ir tą patį vamzdyną, jei
pirmasis yra prieš srovę, ir
antrasis – žemiau, nustatomas lygtis
Bernulis
 ,
,
kur
h2
– h1
- svorio centrų aukščių skirtumas
sekcijos iš savavališkai pasirinktos
horizontalus lygis;
v1,
v2
– vidutiniai alyvos greičiai ruožuose;
g - jėgos pagreitis
gravitacija;

hidrauliniai nuostoliai judėjimo metu
alyvos nuo pirmos sekcijos iki antrojo.
Lygtis
Bernoulli visiškai naudojamas
siurblių siurbimo linijų skaičiavimui;
kitais atvejais pirmasis terminas,
paprastai nepaisoma ir svarstoma:

hidraulinis
nuostoliai dažniausiai skirstomi į vietinius
nuostoliai ir trinties nuostoliai išilgai
vamzdynai (linijiniai).
1.5.1
vietiniai nuostoliai
energijos yra dėl vietinių
hidraulinis pasipriešinimas,
sukeliantis srauto iškraipymą. Vietinis
pasipriešinimai yra: susiaurėjimai,
vamzdynų išplėtimas, apvalinimas,
filtrai, valdymo įranga ir
reguliavimas ir tt Kai teka
skysčių per vietines varžas
jo greitis kinta ir dažniausiai būna
dideli sūkuriai.
Nuostoliai
spaudimas dėl vietinių pasipriešinimų
nustatoma pagal formulę Weisbachas:
 MPa
MPa
(arba
 Pa),
Pa),
kur

praradimas,
v
yra vidutinis srauto greitis per skerspjūvį
vamzdyje už vietinės varžos, m/s;
,
N/m3;
g=9,81 m/s2.
kiekviena
būdingas vietinis pasipriešinimas
pagal jo koeficiento vertę

Esant audringam srautui, vertės
pasipriešinimo ir keičiasi labai mažai
pasikeitus atkarpos dydžiui, greičiui
skysčio srautas ir klampumas. Taigi
manyti, kad jie nepriklauso nuo skaičiaus
Reinoldsas Re.
Vertybės

pavyzdžiui, trišakiams su tokiais pat
kanalo skersmuo yra lygus,
jei:
srautai
sumuoti, skirtis; srautas
pravažiavimas;









adresu
vamzdžio lenkimas

Vertybės

įrangos hidraulinėse sistemose, paimtos iš
informacinė literatūra.
At
laminarinis srautas (Re
Nuostoliai
slėgis iš vietinių pasipriešinimų ties
laminarinis srautas nustatomas pagal
formulė:
 MPa
MPa
kur

= a

Kiekiai
Standartinis slėgio praradimas
hidrauliniai įtaisai, skirti
paprastai vardinis srautas
išvardytos jų techninėse specifikacijose.
1.5.2
Pralaimėjimas
ilgio trintis
yra energijos praradimas, kuris atsiranda
tiesiuose pastovaus skerspjūvio vamzdžiuose,
tie. su vienodu skysčio srautu,
ir didėja proporcingai ilgiui
vamzdžiai. Šie nuostoliai atsiranda dėl vidinių
trinties skystyje, todėl turi
įdėkite į šiurkščius ir lygius vamzdžius.
Nuostoliai
vamzdyno trinties slėgis
nustatoma pagal formulę Darcy:
 MPa
MPa
kur

l
ir d
- vamzdyno ilgis ir vidinis skersmuo,
mm.
Tai
formulė tinka tiek laminariniam,
taip pat turbulentiniame sraute; skirtumas
susideda tik iš koeficiento verčių

At
laminarinis srautas (Re
At
turbulentinio srauto trinties koeficientas
yra ne tik Re funkcija, bet
taip pat priklauso nuo vidinio šiurkštumo
vamzdžio paviršius. Dėl hidrauliškai
sklandžiai vamzdžiai,
tie. su šiurkštumu, kad
praktiškai neturi įtakos jo atsparumui,
turbulentinės trinties koeficientas
režimą galima nustatyti pagal formulę PC.
Konakova:

vamzdis
laikomas hidrauliniu lygiu, jei
(d/k)>(Re/20),
kur k yra lygiavertis šiurkštumas,
mm. Pavyzdžiui, naujam besiūliui plienui
vamzdžiai k≈0,03
mm, o po kelerių metų eksploatacijos
k≈0,2
mm, naujiems besiūliams vamzdžiams iš
spalvotųjų metalų k≈0,005
mm. Šie vamzdžiai dažnai naudojami
staklių hidraulinės sistemos.
Koeficientas
trintis turbulentiniame režime gali būti
nustatyti pagal formulę Altšulija,
yra universalus (t. y. taikomas
bet kuriuo atveju):

2. Dujotiekio srauto modulio srauto charakteristikos
Prisiminkime
tiesinio nuostolio formulė – Darcy formulė
– Veisbachas:
 .
.
Express
šioje formulėje greitis V
per srautą Q
nuo santykio
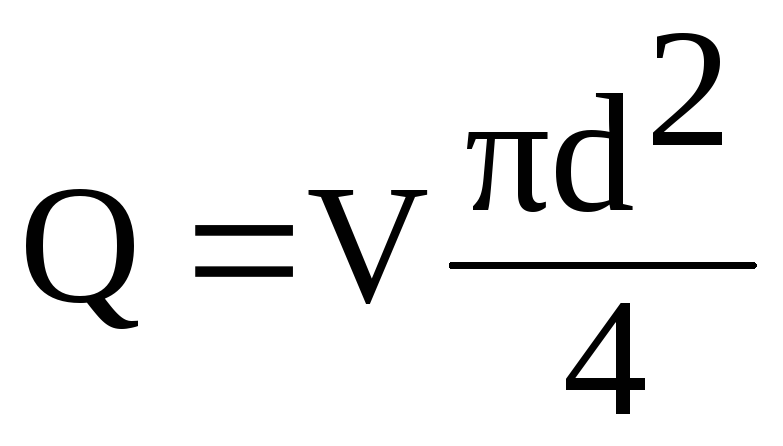
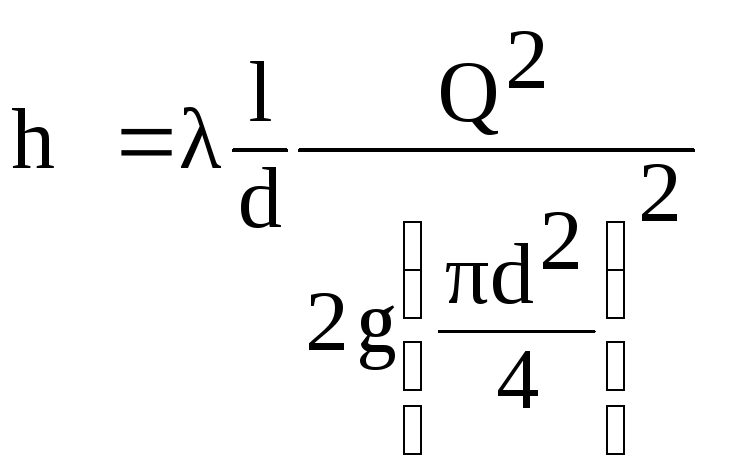
(6.1)
Dėl
tam tikro skersmens vamzdynas
kiekių kompleksas
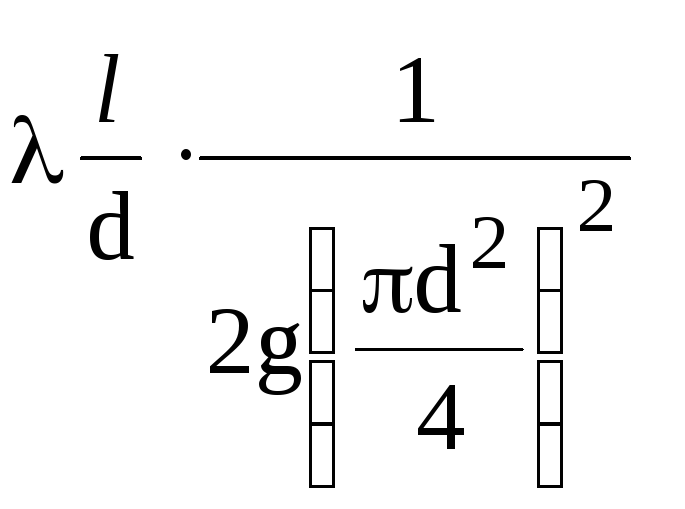
konstanta (1/K2),
išskyrus hidraulinį koeficientą
trintis λ. Remiantis koncepcija
vidutinis ekonominis greitis Vs.e
parodykime, kad nurodytas koeficientas λ
galima priskirti šiam kompleksui, nes v
Šiuo atveju Reinoldso skaičius bus
turi konkrečią reikšmę:
 ,
,
o Nikuradze sklype – koeficientas λ in
šis atvejis turės konkretų
prasmė.
Pateisinti
sąvokos įvedimo teisėtumas
vidutinis ekonominis greitis taip
samprotavimus.
hidraulinis
sistema, pvz., vandentiekis,
galite praleisti tam tikras išlaidas
pagaminti iš skirtingo skersmens vamzdžių. At
Tuo pačiu metu, padidėjus skersmeniui d,
todėl greitis V sumažėjo
didės kapitalo išlaidos, ir
veiklos sąnaudos
sumažėjimas dėl sumažėjusio hidraulinio
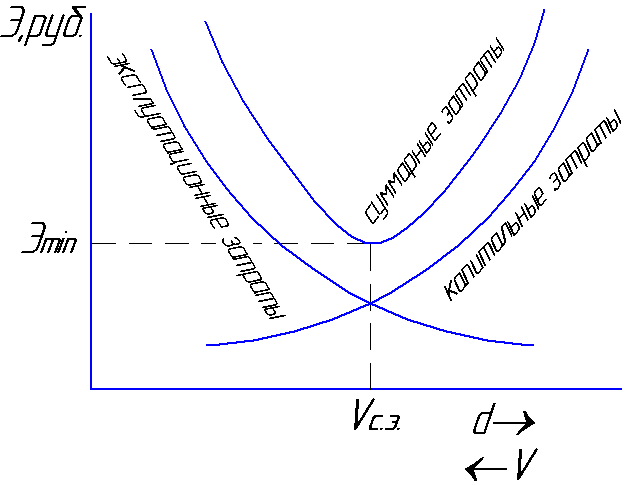
nuostoliai. Greitis, kuriuo bendras
išlaidos bus minimalios
bus vadinamas vidutiniu ekonominiu
greitis Vs.e
= 0,8 ... 1,3 m / s (6.1 pav.).
pav.6.1
Tada
tiesinių nuostolių formulė (6.1) įgauna formą
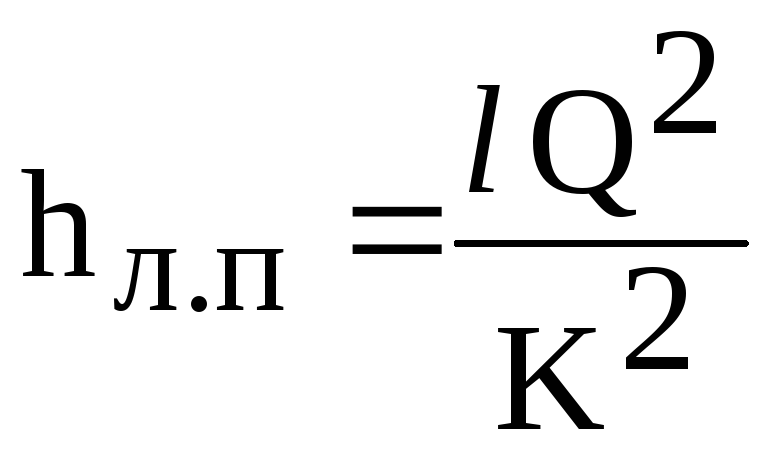
(6.2)
kur
K - dujotiekio charakteristika
(srauto modulis), priklauso nuo medžiagos
vamzdynas, skersmuo ir srautas. yra paimtas
iš lentelių.
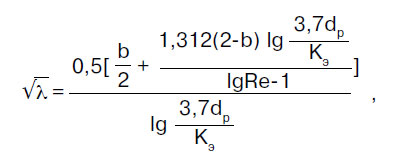
 ), C
), C ,
,