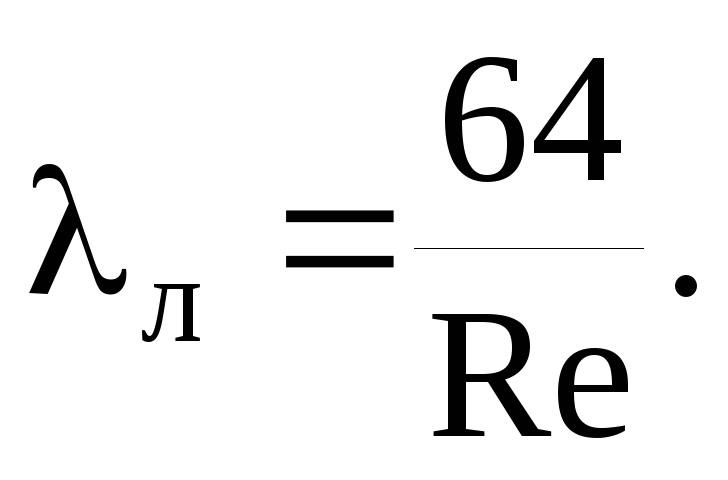1. Hidrostatiskais spiediens
Hidrostatiskais spiediens ir
iekšējais spiedes spēks sakarā ar
iedarbojoties uz ārējiem spēkiem
dots punkts šķidrumā. Tāds spiediens
visos virzienos ir vienāds un atkarīgs
par punkta stāvokli šķidrumā miera stāvoklī.
Hidrostatiskā spiediena izmēri
MKGSS sistēmā - kg / cm2 vai t / m2,
SI sistēmā - N/m2.
Pamatvienību attiecības
spiediens:
|
kg/cm2 |
N/m2 |
|
|
tehniskā atmosfēra |
1 |
98066,5 |
|
milimetrs ūdens staba |
0,0001 |
9,80665 |
|
dzīvsudraba staba milimetrs |
0,00136 |
133,32 |
Praktiskajos aprēķinos 1 tehniskais
atmosfēra \u003d 1 kg / cm2 \u003d 10 m ūdens. Art. =
735 mmHg Art. = 98070 N/m2.
Nesaspiežamam šķidrumam, kas ir
līdzsvarā zem spēka
gravitācija, pilna hidrostatiska
punkta spiediens:
p=p+

kur p ir spiediens uz brīvo
šķidruma virsma;

augstums h ar laukumu
šķērsgriezums vienāds ar vienu;
h - iegremdēšanas dziļums
punktus;

Dažiem šķidrumiem vērtības
risināšanā izmantotais īpatnējais svars
uzdevumi ir doti pielikumā (tab.
P-3).
Virsspiediena vērtība virs
atmosfēras (lppa)
sauc par manometrisko vai
pārspiediens:

Ja spiediens uz brīvo virsmu
vienāds ar atmosfēras, tad lieko
spiediens lppm=

Zem atmosfēras spiediena
daudzumu sauc par vakuumu:
Rbaiss= pa- R.
Risinājums lielākajai daļai šo problēmu
sadaļa ir saistīta ar lietošanu
hidrostatikas pamatvienādojums

kur z ir koordināte vai
punkta atzīme.
1. Vispārīga informācija par cauruļvadu hidraulisko aprēķinu
Aprēķinot
tiek apsvērti cauruļvadi
vienmērīgs, vienmērīgs spiediens
jebkura šķidruma kustība
vētrains režīms, apaļi cilindriski
caurules. Šķidrums spiediena caurulēs
ir zem spiediena un
to šķērsgriezumi ir pilnībā
piepildīta. Šķidruma kustība gar
rezultātā rodas cauruļvads
to, ka spiediens tās sākumā ir lielāks nekā
beigās.
Hidrauliskais
aprēķins tiek veikts, lai noteiktu
cauruļvada diametrs d
ar zināmu
garums, lai nodrošinātu izlaišanu
noteiktu plūsmas ātrumu J
vai izveido
noteiktā diametrā un vajadzīgā garumā
spiediens un šķidruma plūsma. Cauruļvadi
atkarībā no to garuma un modeļa
vietas ir sadalītas vienkāršās
un sarežģīti. Uz vienkāršiem cauruļvadiem
ietver cauruļvadus, kuriem nav
zari gar garumu, ar konstantu
tie paši izdevumi.
Cauruļvadi
sastāv no tāda paša diametra caurulēm
visā garumā vai no dažādu cauruļu sekcijām
diametri un garumi. Pēdējais gadījums
attiecas uz seriālo savienojumu.
Vienkārši cauruļvadi
atkarībā no garuma ar zemes gabalu vietējā
pretestības iedala īsos un
garš. īss
cauruļvadi
ir
cauruļvadi ar pietiekami īsu garumu,
kurā vietējā pretestība
veido vairāk nekā 10% hidrauliskās
garuma zudums. Piemēram, tie ietver:
sifona caurules, iesūkšana
lāpstiņu sūkņu caurules, sifoni (spiediens
ūdensvadi zem ceļa uzbēruma),
cauruļvadi ēku un būvju iekšpusē
utt.
garš
cauruļvadi
sauca
cauruļvadi ir salīdzinoši lieli
garumi, kuros galvas zudums visā garumā
ievērojami pārsniedz vietējo
zaudējumiem. Vietējie zaudējumi ir
mazāk par 5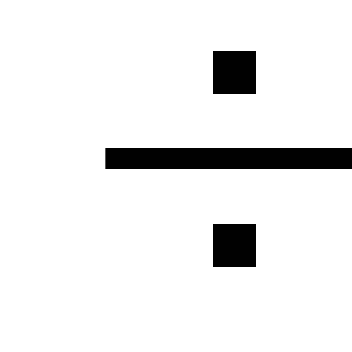
zudumi cauruļvada garumā, un tāpēc
tos var atstāt novārtā vai ieviest plkst
hidrauliskie aprēķini pieaug
koeficients vienāds ar 1,05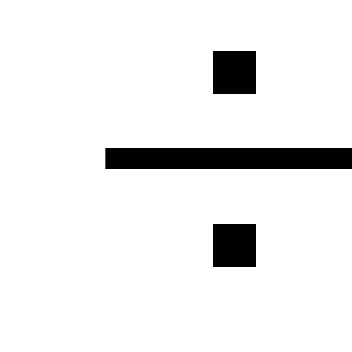
Sistēmā iekļūst gari cauruļvadi
ūdensapgādes tīkli, sūknēšanas caurules
stacijas, cauruļvadi un cauruļvadi
rūpniecības uzņēmumiem un
lauksaimniecības mērķim un
utt.
Sarežģīti cauruļvadi
ir dažādi zari visā garumā,
tie. cauruļvads sastāv no cauruļu tīkla
noteikti diametri un garumi. Komplekss
cauruļvadi ir sadalīti
paralēls, strupceļš (sazarots),
gredzenveida (slēgtie) cauruļvadi,
iekļauts ūdens apgādes tīklā.
Hidrauliskais
cauruļvada aprēķins tiek samazināts kā
parasti, lai atrisinātu trīs galvenās problēmas:
-
definīcija
cauruļvada plūsma J,
ja zināms
spiedienu H,
garums l
un diametrs d
cauruļvads,
ņemot vērā dažu vietējo pieejamību
pretestības vai to neesamības gadījumā; -
definīcija
nepieciešamais spiediens H,
nepieciešams caurlaides nodrošināšanai
zināmā plūsma J
pa cauruļvadu
garš l
un diametrs d; -
definīcija
cauruļvada diametrs d
kad
zināmās galvas vērtības H,
izdevumi J
un garums l.
Šķidruma plūsmas ātrums ir
kur q > aprēķinātā šķidruma plūsma, m3/s;
- caurules dzīvās daļas laukums, m2.
Berzes pretestības koeficientu λ nosaka saskaņā ar noteikumu kopuma SP 40-102-2000 “Polimērmateriālu ūdensapgādes un kanalizācijas sistēmu cauruļvadu projektēšana un uzstādīšana” noteikumiem. Vispārīgās prasības":
kur b ir kāds šķidruma plūsmas režīmu līdzības skaitlis; ja b > 2, ņem b = 2.
kur Re ir faktiskais Reinoldsa skaitlis.
kur ν ir šķidruma kinemātiskās viskozitātes koeficients, m²/s. Aprēķinot aukstā ūdens caurules, tas tiek ņemts vienāds ar 1,31 10-6 m² / s - ūdens viskozitāte +10 ° C temperatūrā;
Rekv > - Reinoldsa skaitlis, kas atbilst hidrauliskās pretestības kvadrātiskā apgabala sākumam.
kur Ke ir caurules materiāla hidrauliskais raupjums, m Caurulēm, kas izgatavotas no polimērmateriāliem, ņem Ke = 0,00002 m, ja caurules ražotājs nenorāda citas raupjuma vērtības.
Tajos plūsmas gadījumos, kad Re ≥ Rekv, parametra b aprēķinātā vērtība kļūst vienāda ar 2, un formula (4) tiek ievērojami vienkāršota, pārvēršoties par labi zināmo Prandtla formulu:
Pie Ke = 0,00002 m kvadrātiskās pretestības apgabals rodas pie ūdens plūsmas ātruma (ν = 1,31 10-6 m²/s), kas vienāds ar 32,75 m/s, kas sabiedriskās ūdensapgādes sistēmās praktiski nav sasniedzams.
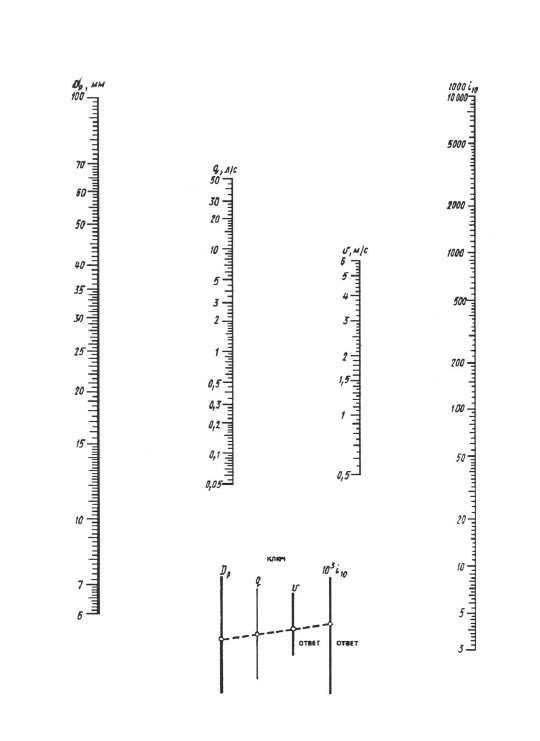
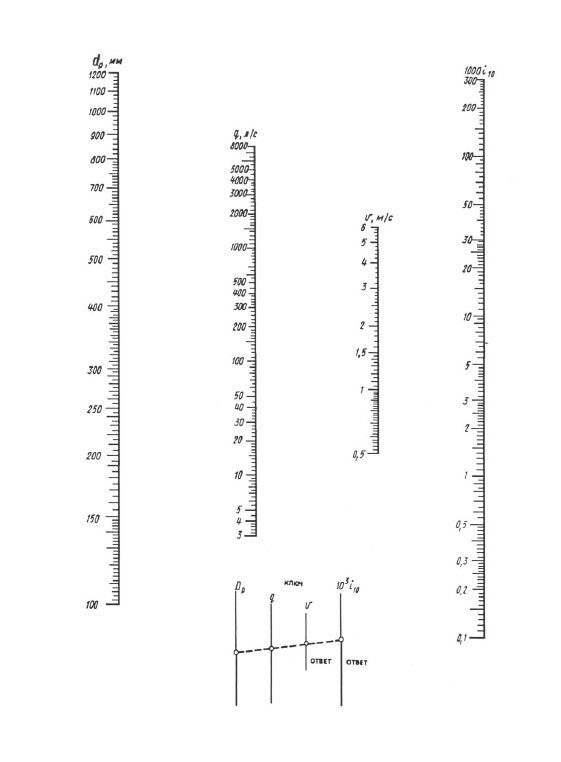
Ikdienas aprēķiniem ieteicamas nomogrammas, bet precīzākiem aprēķiniem - "No polimērmateriāliem izgatavotu cauruļvadu hidraulisko aprēķinu tabulas", 1. sējums "Spiediena cauruļvadi" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
Aprēķinot pēc nomogrammām, rezultāts tiek sasniegts ar vienu lineāla pārklājumu - jums vajadzētu savienot punktu ar aprēķinātā diametra vērtību dp skalā ar punktu ar aprēķinātā plūsmas ātruma vērtību uz q (l / s) mērogu ar taisni, turpina šo taisni, līdz tā krustojas ar ātruma V un īpatnējo zudumu augstuma skalām 1000 i (mm/m). Taisnes krustošanās punkti ar šīm skalām dod vērtību V un 1000 i.
Kā zināms, elektroenerģijas izmaksas šķidruma sūknēšanai ir tieši proporcionālas H vērtībai (ceteris paribus). Aizvietojot izteiksmi ( 3 ) formulā ( 2 ), ir viegli redzēt, ka i (un līdz ar to H) vērtība ir apgriezti proporcionāla aprēķinātajam diametram dp līdz piektajai pakāpei.
Iepriekš ir parādīts, ka dp vērtība ir atkarīga no caurules sienas biezuma e: jo plānāka ir siena, jo lielāks dp un attiecīgi mazāks spiediena zudums berzes dēļ un elektroenerģijas izmaksas.
Ja kāda iemesla dēļ mainās caurules MRS vērtība, tās diametrs un sienas biezums (SDR) ir jāpārrēķina.
Jāpatur prātā, ka vairākos gadījumos cauruļu ar MRS 10 izmantošana cauruļu ar MRS 8 vietā, īpaši caurulēm ar MRS 6.3, ļauj samazināt cauruļvada diametru par vienu izmēru. Tāpēc mūsu laikā polietilēna PE 80 (MRS 8) un PE 100 (MRS 10) izmantošana polietilēna PE 63 (MRS 6.3) vietā cauruļu ražošanā ļauj ne tikai samazināt cauruļu sieniņu biezumu, to svaru. un materiālu patēriņu, bet arī samazināt enerģijas izmaksas šķidruma sūknēšanai (ceteris paribus).
Pēdējos gados (pēc 2013. gada) PE80 polietilēna caurules no ražošanas gandrīz pilnībā ir aizstātas ar PE100 polietilēna caurulēm. Tas izskaidrojams ar to, ka izejvielas, no kurām izgatavotas caurules, tiek piegādātas no ārvalstīm ar zīmolu PE100.Un arī ar to, ka polietilēnam 100 ir vairāk stiprības raksturlielumu, kā rezultātā tiek ražotas caurules ar tādām pašām īpašībām kā PE80 caurulēm, bet ar plānāku sienu, tādējādi palielinot polietilēna cauruļvadu caurlaidspēju.
Nomogramma spiediena zudumu noteikšanai caurulēs ar diametru 6 100 mm.
Nomogramma spiediena zudumu noteikšanai caurulēs ar diametru 100, 1200 mm.
Reinoldsa kritērijs
Šo atkarību atklāja angļu fiziķis un inženieris Osborns Reinoldss (1842-1912).
Kritērijs, kas palīdz atbildēt uz jautājumu par to, vai ir jāņem vērā viskozitāte, ir Reinoldsa skaitlis Re. Tas ir vienāds ar plūstoša šķidruma elementa kustības enerģijas attiecību pret iekšējo berzes spēku darbu.
Apsveriet kubiskā šķidruma elementu ar malas garumu n. Elementa kinētiskā enerģija ir:
Saskaņā ar Ņūtona likumu berzes spēku, kas iedarbojas uz šķidruma elementu, definē šādi:
Šī spēka darbs, pārvietojot šķidruma elementu attālumā n ir
un šķidruma elementa kinētiskās enerģijas attiecība pret berzes spēka darbu ir
Mēs samazinām un iegūstam:
Re sauc par Reinoldsa numuru.
Tādējādi Re ir bezizmēra lielums, kas raksturo viskozo spēku relatīvo lomu.
Piemēram, ja korpusa izmēri, ar kuriem saskaras šķidrums vai gāze, ir ļoti mazi, tad pat ar zemu viskozitāti Re būs nenozīmīgs un dominējošā loma ir berzes spēkiem. Gluži pretēji, ja korpusa izmēri un ātrums ir lieli, tad Re >> 1 un pat liela viskozitāte gandrīz nekādi neietekmēs kustības raksturu.
Tomēr ne vienmēr lielie Reinoldsa skaitļi nozīmē, ka viskozitātei nav nekādas nozīmes. Tātad, kad tiek sasniegta ļoti liela (vairāki desmiti vai simti tūkstoši) Re skaitļa vērtība, gluda lamināra (no latīņu valodas lamina - "plāksne") plūsma pārvēršas nemierīgā (no latīņu valodas turbulentus - "vētraina"). , “haotisks”), ko pavada haotiskas, nestabilas kustības šķidrumi. Šo efektu var novērot, pakāpeniski atverot ūdens krānu: tieva straume parasti plūst vienmērīgi, bet, palielinoties ūdens ātrumam, plūsmas vienmērīgums tiek traucēts. Strūklā, kas izplūst zem augsta spiediena, šķidruma daļiņas pārvietojas nejauši, svārstās, visu kustību pavada spēcīga sajaukšanās.
Turbulences parādīšanās ievērojami palielina pretestību. Cauruļvadā turbulentās plūsmas ātrums ir mazāks par laminārās plūsmas ātrumu pie tādiem pašiem spiediena kritumiem. Bet turbulence ne vienmēr ir slikta. Sakarā ar to, ka sajaukšanās turbulences laikā ir ļoti nozīmīga, siltuma pārnese - pildvielu dzesēšana vai sildīšana - notiek daudz intensīvāk; ķīmiskās reakcijas izplatās ātrāk.
Bernulli stacionārās kustības vienādojums
Vienu no svarīgākajiem hidromehānikas vienādojumiem 1738. gadā ieguva Šveices zinātnieks Daniels Bernulli (1700-1782). Vispirms viņam izdevās aprakstīt ideāla šķidruma kustību, kas izteikta Bernulli formulā.
Ideāls šķidrums ir šķidrums, kurā nav berzes spēku starp ideālā šķidruma elementiem, kā arī starp ideālo šķidrumu un trauka sienām.
Stacionārās kustības vienādojums ar viņa nosaukumu ir:
kur P ir šķidruma spiediens, ρ ir tā blīvums, v ir kustības ātrums, g ir brīvā kritiena paātrinājums, h ir augstums, kurā atrodas šķidruma elements.
Bernulli vienādojuma nozīme ir tāda, ka sistēmā, kas piepildīta ar šķidrumu (cauruļvada sekcija), katra punkta kopējā enerģija vienmēr nemainās.
Bernulli vienādojumam ir trīs termini:
- ρ⋅v2/2 - dinamiskais spiediens - kinētiskā enerģija uz braukšanas šķidruma tilpuma vienību;
- ρ⋅g⋅h - svara spiediens - šķidruma tilpuma vienības potenciālā enerģija;
- P - statiskais spiediens, pēc savas izcelsmes ir spiediena spēku darbs un tas neatspoguļo kāda īpaša enerģijas veida rezervi (“spiediena enerģija”).
Šis vienādojums izskaidro, kāpēc šauros caurules posmos plūsmas ātrums palielinās un spiediens uz caurules sienām samazinās. Maksimālais spiediens caurulēs tiek iestatīts precīzi vietā, kur caurulei ir vislielākais šķērsgriezums. Šaurās caurules daļas šajā ziņā ir drošas, taču spiediens tajās var nokrist tik ļoti, ka šķidrums uzvārās, kas var izraisīt kavitāciju un caurules materiāla iznīcināšanu.
Navjē-Stoksa vienādojums viskoziem šķidrumiem
Stingrākā formulējumā viskozās berzes lineāro atkarību no šķidruma ātruma izmaiņām sauc par Navjē-Stoksa vienādojumu. Tas ņem vērā šķidrumu un gāzu saspiežamību un atšķirībā no Ņūtona likuma ir spēkā ne tikai cieta ķermeņa virsmas tuvumā, bet arī katrā šķidruma punktā (netālu no cieta ķermeņa virsmas, ja tas ir nesaspiežams). šķidrums, Navjē-Stoksa vienādojums un Ņūtona likums sakrīt).
Jebkuras gāzes, kurām ir izpildīts nepārtrauktas vides nosacījums, arī atbilst Navjē-Stoksa vienādojumam, t.i. ir Ņūtona šķidrumi.
Šķidrumu un gāzu viskozitāte parasti ir ievērojama pie salīdzinoši maziem ātrumiem, tāpēc dažkārt tiek teikts, ka Eilera hidrodinamika ir īpašs (ierobežojošs) Navjē-Stoksa hidrodinamikas lielu ātrumu gadījums.
Pie maziem ātrumiem, saskaņā ar Ņūtona viskozās berzes likumu, ķermeņa pretestības spēks ir proporcionāls ātrumam. Lielā ātrumā, kad viskozitāte pārstāj spēlēt nozīmīgu lomu, ķermeņa pretestība ir proporcionāla ātruma kvadrātam (ko pirmais atklāja un pamatoja Ņūtons).
Hidrauliskā aprēķinu secība
1.
Tiek izvēlēta galvenā tirāža
gredzenveida apkures sistēma (lielākā daļa
neizdevīgi atrodas hidrauliskajā
attiecības). Divu cauruļu strupceļā
sistēmas ir gredzens, kas iet cauri
apakšējais instruments no visattālākajiem un
noslogots stāvvads, viencaurulē -
caur attālāko un ielādētu
stāvvads.
Piemēram,
divu cauruļu apkures sistēmā ar
augšējā vadu galvenā cirkulācija
gredzens pāries no siltuma punkta
caur galveno stāvvadu, padeves līniju,
caur attālāko stāvvadu, apkure
lejas iekārta, atgriešanas līnija
uz siltumpunktu.
V
sistēmas ar saistīto ūdens kustību iekšā
gredzens tiek ņemts par galveno,
visvairāk iet cauri vidum
piekrauts statīvs.
2.
Galvenais cirkulācijas gredzens saplīst
sižetos (sižetu raksturo
pastāvīga ūdens plūsma un tas pats
diametrs). Diagramma parāda
sekciju numuri, to garumi un termiskais
slodzes. Maģistrāles termiskā slodze
parauglaukumus nosaka summējot
termiskās slodzes, ko tie apkalpo
zemes gabali. Lai izvēlētos caurules diametru
tiek izmantoti divi daudzumi:
a)
dotā ūdens plūsma;
b)
aptuvenie specifiskie spiediena zudumi
berzei dizaina apritē
gredzens RTr.
Priekš
aprēķins Rcp
jāzina galvenā garums
cirkulācijas gredzens un aprēķināts
cirkulācijas spiediens.
3.
Aprēķinātā tirāža
formulas spiediens
 ,
,
(5.1)
kur
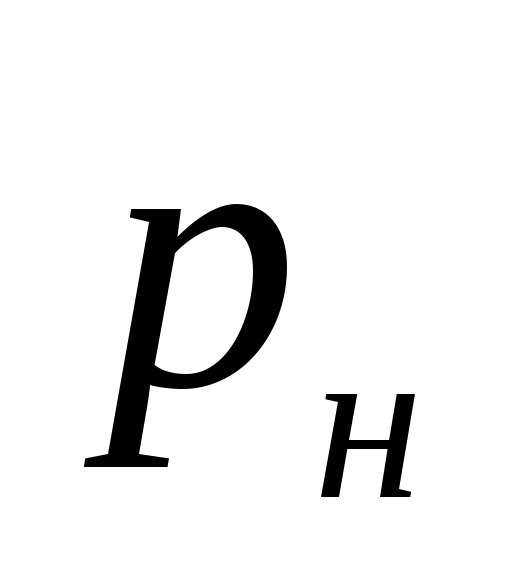
sūkņa radītais spiediens, Pa.
Sistēmas projektēšanas prakse
apkure parādīja, ka visvairāk
vēlams izmērīt sūkņa spiedienu,
vienāds
 ,
,
(5.2)
kur
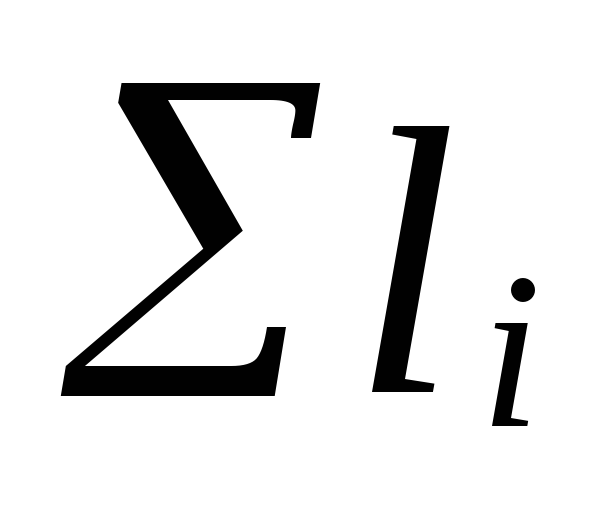
galvenā tirāžas posmu garumu summa
gredzeni;
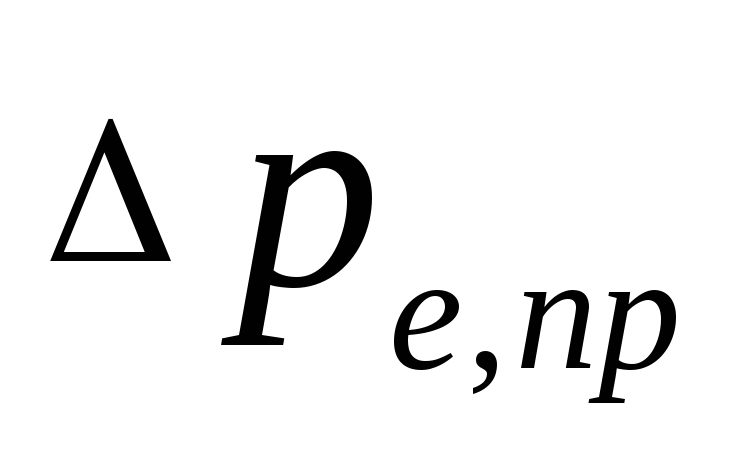
dabiskais spiediens, kas rodas, kad
ūdens dzesēšana iekārtās, Pa, iespējama
noteikt, kā
 ,
,
(5.3)
kur
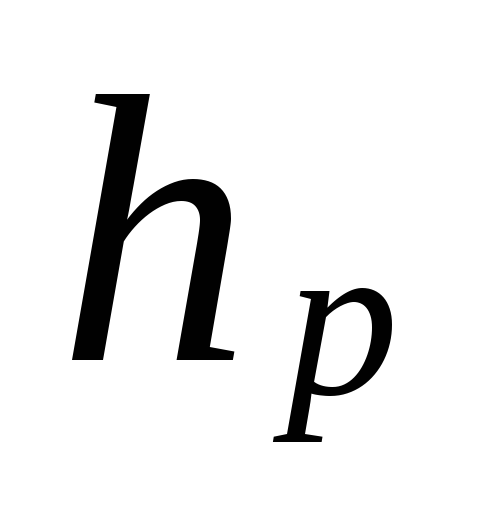
attālums no sūkņa centra (lifta)
līdz apakšējā stāva ierīces centram, m.
Nozīme
koeficients iespējams
nosaka no 5.1. tabulas.
tabula
5.1. Nozīme c
atkarībā no projektētās temperatūras
ūdens apkures sistēmā
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
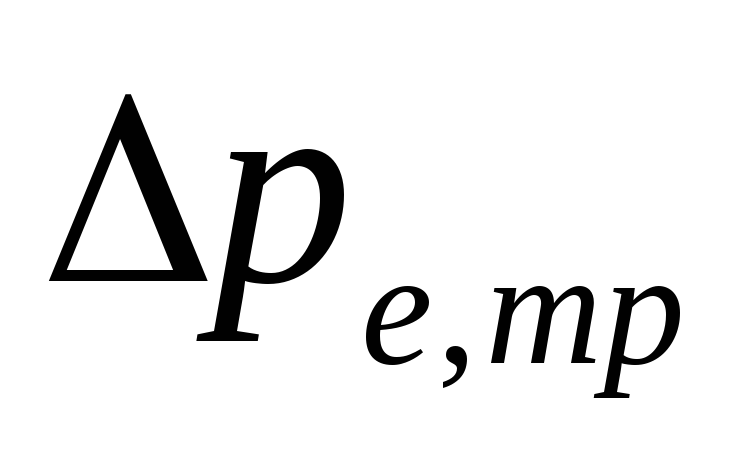
dabiskais spiediens iekšā
ūdens dzesēšanas rezultātā cauruļvados
.
V
sūknēšanas sistēmas ar apakšējo vadu
lielums
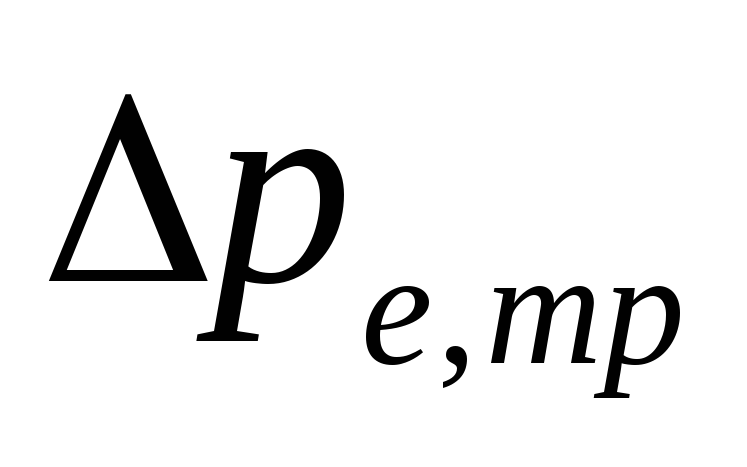
-
Ir noteikti
īpatnējais berzes spiediena zudums
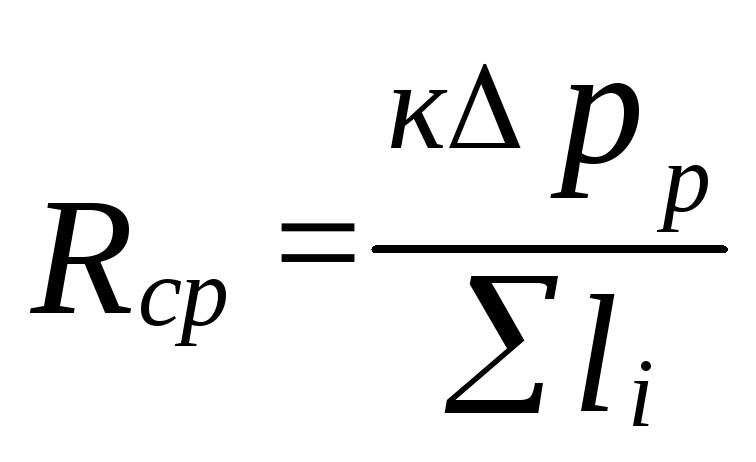
(5.4)
kur
k=0,65 nosaka spiediena zudumu proporciju
berzei.
5.
Ūdens plūsmu teritorijā nosaka
formula
 (5.5)
(5.5)
kur
J
- siltuma slodze objektā, W:
(tG
— tO)
- dzesēšanas šķidruma temperatūras starpība.
6.
Pēc lieluma
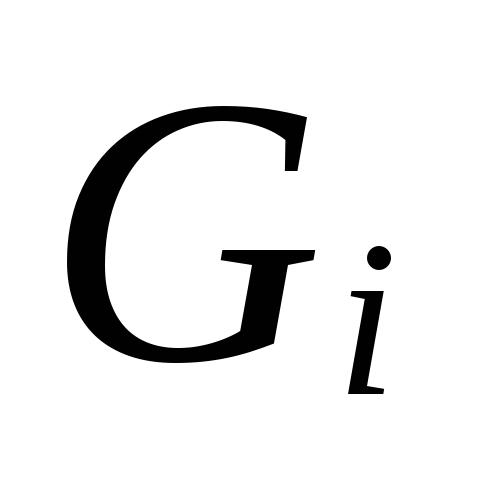
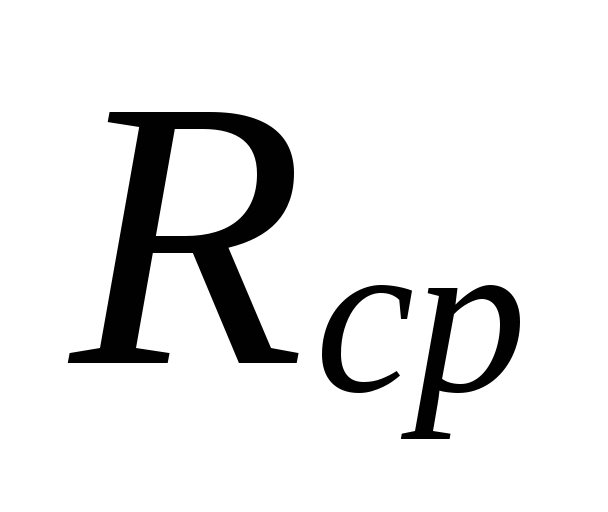
.

6.
Izvēlētajiem cauruļvadu diametriem
un tiek noteikts paredzamais ūdens patēriņš
dzesēšanas šķidruma ātrums v
un faktiskā specifiskā
berzes spiediena zudums Rf.
Plkst
diametru izvēle apgabalos ar mazu
dzesēšanas šķidruma plūsmas ātrumi var būt
lielas neatbilstības starp
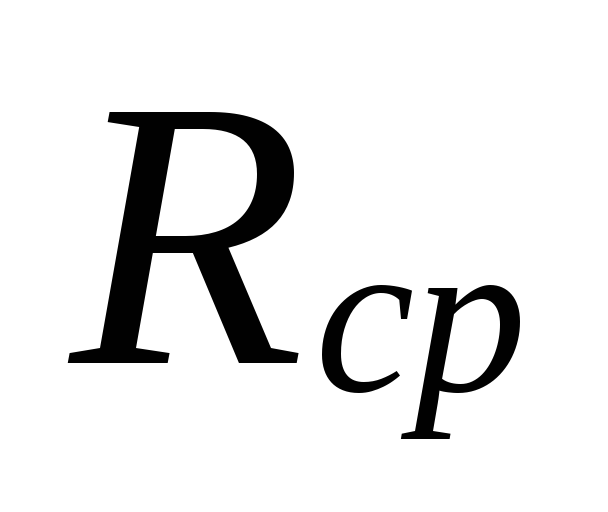
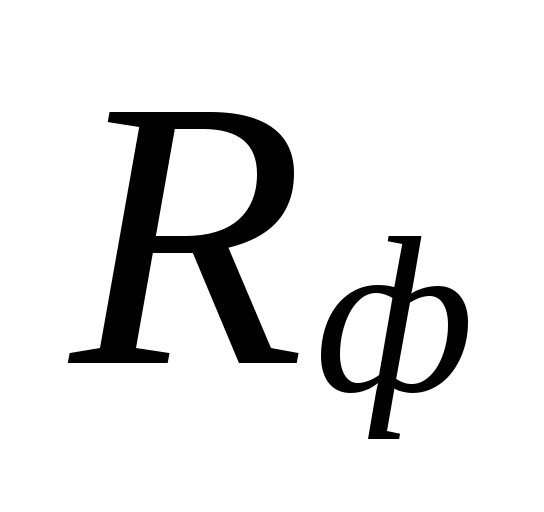
nepietiekami novērtēti zaudējumi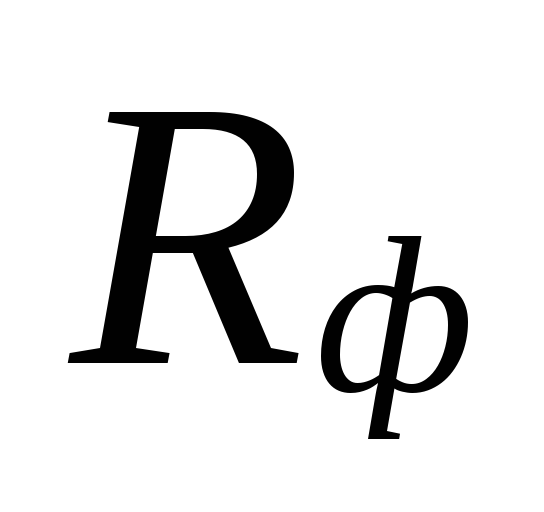
šīs jomas tiek kompensētas ar pārvērtēšanu
daudzumus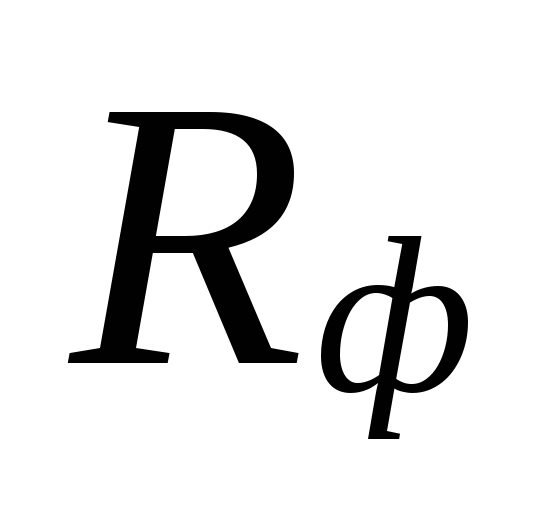
7.
Tiek noteikti berzes spiediena zudumi
uz aprēķināto platību, Pa:
 .
.
(5.6)
rezultātus
aprēķini ievadīti 5.2. tabulā.
8.
Spiediena zudumi lokāli
pretestības, izmantojot vienu formulu:
 ,
,
(5.7)
kur
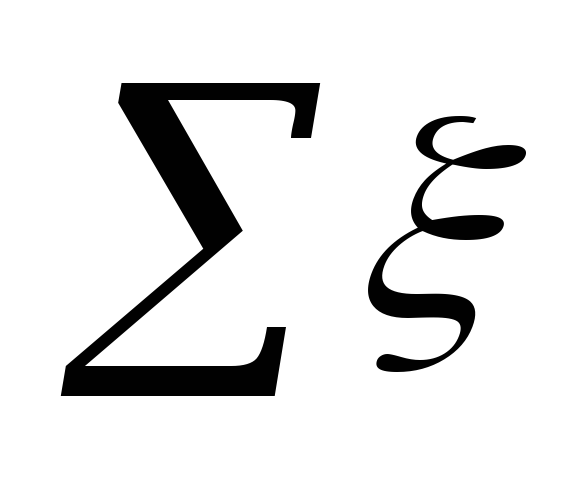
apdzīvotās vietas teritorijā.
Nozīme ξ
katrā vietā ir apkopoti tabulā. 5.3.
5.3. tabula -
Vietējie pretestības koeficienti
|
Nr p / lpp |
Vārdi |
Vērtības |
Piezīmes |
9.
Nosakiet kopējo spiediena zudumu
katrā jomā
 .
.
(5.8)
10. Noteikt
kopējais spiediena zudums berzes dēļ un
vietējās pretestībās galvenokārt
cirkulācijas gredzens
 .
.
(5.9)
11. Salīdziniet Δp
Ar ΔpR.
Kopējais spiediena zudums visā gredzenā
jābūt mazākam par ΔpR
uz
 .
.
(5.10)
vienreizējās lietošanas krājumi
ir nepieciešams spiediens uz neuzskaitīto in
hidrauliskās pretestības aprēķins.
Ja apstākļi nav
tiek veiktas, dažiem tas ir nepieciešams
gredzena sekcijas, lai mainītu cauruļu diametrus.
12. Pēc aprēķina
galvenais cirkulācijas gredzens
izveidojiet atlikušo gredzenu savienojumu. V
tikai katrs jauns gredzens
papildu nekoplietojamās telpas,
savienots paralēli sekcijām
galvenais gredzens.
Zaudējumu neatbilstība
spiediens uz paralēli savienotiem
zemes gabali atļauti līdz 15% ar strupceļu
ūdens kustība un līdz 5% - ar garām.
tabula
5.2 - Hidrauliskā aprēķina rezultāti
apkures sistēmai
|
Uz |
Autors |
Autors |
||||||||||||||
|
Numurs |
termiski |
Patēriņš |
Garums |
Diametrs |
Ātrums |
Konkrēts |
Zaudējumi |
Summa |
Zaudējumi |
d, |
v, |
R, |
Δptr, |
∑ξ |
Z, |
Rl+Z, |
6. nodarbība
Gāzes temperatūras maiņa visā gāzes vada garumā
Stacionārā gāzes plūsmā masa
plūsmas ātrums gāzes vadā ir
 . (2.41)
. (2.41)
Faktiski gāzes kustība gāzes vadā
vienmēr nav izotermisks. V
Kompresijas laikā gāze uzsilst.
Pat pēc tā dzesēšanas COP, temperatūra
gāzes iekļūšana cauruļvadā
ir aptuveni 2040С,
kas ir daudz augstāka par temperatūru
vide (T).
Praksē gāzes temperatūra kļūst
tuvu apkārtējās vides temperatūrai
tikai maza diametra gāzes vadiem
(Dy0.
Turklāt jāņem vērā tas
cauruļvadu gāze
ir īsta gāze, kas ir raksturīga
Džoula-Tompsona efekts, kas ņem vērā
siltuma absorbcija gāzes izplešanās laikā.
Kad temperatūra mainās visā garumā
ir aprakstīta gāzes cauruļvada gāzes kustība
vienādojumu sistēma:
specifiskā enerģija ,
,
nepārtrauktība ,
,
štatos ,
,
siltuma bilance .
.
Apsveriet vienādojumu pirmajā tuvinājumā
siltuma bilanci, neņemot vērā efektu
Džouls Tompsons. Vienādojuma integrēšana
siltuma bilance
 ,
,
mēs saņemam
 , (2.42)
, (2.42)
kur ;
;
KSR- vidēji pilns vietnē
siltuma pārneses koeficients no gāzes uz
vide;
G ir gāzes masas plūsmas ātrums;
cP–
gāzes vidējā izobāriskā siltumietilpība.
vērtībatL sauc par bezdimensiju kritēriju
Šuhovs
 (2.43)
(2.43)
Tātad gāzes temperatūra beigās
gāzes vads būs
 . (2.44)
. (2.44)
Attālumā x no sākuma
tiek noteikta gāzesvada gāzes temperatūra
saskaņā ar formulu
 . (2.45)
. (2.45)
Temperatūras izmaiņas visā gāzes vada garumā
ir eksponenciāls (att.
2.6).
Apsveriet
gāzes temperatūras izmaiņu ietekme uz
cauruļvada veiktspēja.
Reizinot abas konkrētā vienādojuma puses
enerģija uz 2 un izsakot ,
,
mēs saņemam
 . (2.46)
. (2.46)
Mēs izsakām gāzes blīvumu kreisajā pusē
izteiksmes (2.46) no stāvokļa vienādojuma
 ,
,
produktswno nepārtrauktības vienādojuma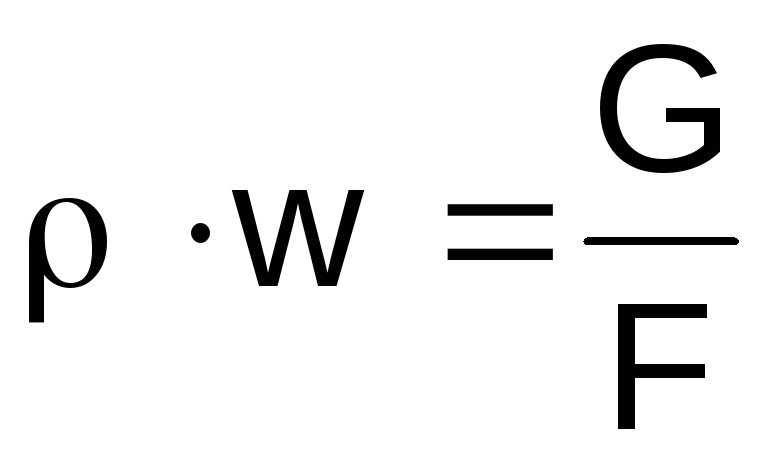
līdzsvaru .
.
Paturot to prātā, īpašais vienādojums
enerģija iegūst formu
 (2.47)
(2.47)
vai
 . (2.48)
. (2.48)
Apzīmējot
 un vienādojuma kreisās puses integrēšana
un vienādojuma kreisās puses integrēšana
(2,48) no PHdoPUZ, un pa labi no THdoTUZ, saņemam
 . (2.49)
. (2.49)
Nomainot
 , (2.50)
, (2.50)
mums ir
 . (2.51)
. (2.51)
Pēc integrācijas norādītajā
robežas, mēs saņemam

 . (2.52)
. (2.52)
Ņemot vērā (2.42)

vai
 , (2.53)
, (2.53)
kur ir korekcijas koeficients, kas ņem vērā
ir korekcijas koeficients, kas ņem vērā
temperatūras izmaiņas visā gāzes vada garumā
(gāzes plūsmas neizotermiskums).
Ņemot vērā (2.53), atkarību noteikšanai
gāzes masas plūsmas ātrums būs formā
 . (2.54)
. (2.54)
Vērtība Hvienmēr lielāks par vienu, tāpēc
gāzes masas plūsmas ātrumu mainot
temperatūra visā gāzes vada garumā
(neizotermisks plūsmas režīms) vienmēr
mazāk nekā izotermiskā režīmā
(T=idem). Produkts THsauc par vidējo integrāli
gāzes temperatūra cauruļvadā.
Ar Šuhova skaitļa vērtībām Shu4
gāzes plūsma cauruļvadā
uzskata par gandrīz izotermisku
pie T=idem. Tāda temperatūra
režīms ir iespējams, sūknējot gāzi ar
zemas gāzes cauruļvadu izmaksas
mazs (mazāks par 500 mm) diametrs līdz ievērojamam
attālums.
Gāzes temperatūras maiņas ietekme
izpaužas Šuhova skaitļa vērtībām
Shu
Plkst
gāzes sūknēšana droseļvārsta klātbūtne
efekts noved pie dziļākas
gāzes dzesēšana nekā tikai ar siltuma apmaiņu
ar augsni. Šajā gadījumā temperatūra
gāze var pat nokrist zemāk
temperatūra T (att.
2.7).
Rīsi. 2.7. Džoula-Tompsona efekta ietekme
par gāzes temperatūras sadalījumu
cauruļvada garums
1 - neņemot vērā Di; 2 - ar
ņemot vērā Di
Tad, ņemot vērā Džoula-Tompsona koeficientu
Temperatūras maiņas likums garumā
ieņem formu
 , (2.55)
, (2.55)
5 Hidrauliskie zudumi
Atšķirība
eļļas spiediens divās daļās vienā
un to pašu cauruļvadu ar nosacījumu
pirmais atrodas augštecē, un
otrais - zemāk, tiek noteikts vienādojums
Bernulli
 ,
,
kur
h2
– h1
- smaguma centru augstumu starpība
sadaļas no patvaļīgi izvēlētas
horizontāls līmenis;
v1,
v2
– vidējie eļļas ātrumi sekcijās;
g - spēka paātrinājums
gravitācija;

hidrauliskie zudumi kustības laikā
eļļas no pirmās sadaļas uz otro.
Vienādojums
Bernulli pilnībā izmantots
sūkņu iesūkšanas līniju aprēķināšanai;
citos gadījumos pirmais termiņš,
parasti tiek atstāti novārtā un ņemti vērā:

hidrauliskais
zaudējumus parasti iedala vietējos
zudumi un berzes zudumi visā garumā
cauruļvadi (lineāri).
1.5.1
vietējie zaudējumi
enerģijas ir vietējās
hidrauliskā pretestība,
izraisot plūsmas traucējumus. Vietējais
pretestības ir: sašaurinājumi,
cauruļvadu paplašināšana, noapaļošana,
filtri, vadības iekārtas un
regulēšana utt Kad plūst
šķidrumi caur vietējām pretestībām
tā ātrums mainās un parasti tādi ir
lieli virpuļi.
Zaudējumi
spiedienu no vietējām pretestībām
nosaka pēc formulas Veisbahs:
 MPa
MPa
(vai
 Pa),
Pa),
kur

zaudējums,
v
ir vidējais plūsmas ātrums šķērsgriezumā
caurulē aiz vietējās pretestības, m/s;
,
N/m3;
g=9,81 m/s2.
Katrs
raksturo vietējo pretestību
pēc tā koeficienta vērtības

Ar turbulentu plūsmu vērtības
pretestība un izmaiņas ļoti maz
mainoties posma izmēram, ātrumam
šķidruma plūsma un viskozitāte. Tātad
pieņemsim, ka tie nav atkarīgi no skaita
Reinolds Re.
Vērtības

piemēram, tees ar tādu pašu
kanālu diametri tiek ņemti vienādi,
ja:
straumes
saskaitīt, atšķirties; plūsma
garāmejot;









plkst
caurules līkums

Vērtības

iekārtu hidrauliskajās sistēmās, ņemtas no
uzziņu literatūra.
Plkst
laminārā plūsma (Re
Zaudējumi
spiediens no vietējām pretestībām plkst
lamināro plūsmu nosaka
formula:
 MPa
MPa
kur

= a

Daudzumi
spiediena zudums standartā
hidrauliskās ierīces
parasti nominālais plūsmas ātrums
norādītas to tehniskajās specifikācijās.
1.5.2
Zaudējums uz
garuma berze
ir enerģijas zudumi, kas rodas
taisnās caurulēs ar nemainīgu šķērsgriezumu,
tie. ar vienmērīgu šķidruma plūsmu,
un palielinās proporcionāli garumam
caurules. Šie zaudējumi ir saistīti ar iekšējiem
berze šķidrumā, un tāpēc ir
novietojiet gan raupjās, gan gludajās caurulēs.
Zaudējumi
cauruļvada berzes spiediens
tiek noteikts pēc formulas Dārsijs:
 MPa
MPa
kur

l
un d
- cauruļvada garums un iekšējais diametrs,
mm.
Šis
formula ir piemērojama gan laminārajai,
kā arī turbulentā plūsmā; atšķirība
sastāv tikai no koeficienta vērtībām

Plkst
laminārā plūsma (Re
Plkst
turbulentās plūsmas berzes koeficients
ir ne tikai Re funkcija, bet
atkarīgs arī no iekšpuses raupjuma
caurules virsma. Priekš hidrauliski
gluda caurules,
tie. ar raupjumu, ka
praktiski neietekmē tā pretestību,
turbulentās berzes koeficients
režīmu var noteikt pēc formulas PC.
Konakova:

caurule
tiek uzskatīts par hidrauliski gludu, ja
(d/k)>(Re/20),
kur k ir līdzvērtīgs raupjums,
mm. Piemēram, jaunam bezšuvju tēraudam
caurules k≈0,03
mm, un pēc vairāku gadu darbības
k≈0,2
mm, jaunām bezšuvju caurulēm, kas izgatavotas no
krāsainie metāli k≈0,005
mm. Šīs caurules bieži izmanto
darbgaldu hidrauliskās sistēmas.
Koeficients
berze turbulentā režīmā var būt
nosaka pēc formulas Altšuļa,
ir universāls (t.i., piemērojams
jebkurā gadījumā):

2. Cauruļvada plūsmas moduļa plūsmas raksturlielumi
Atcerēsimies
lineāro zudumu formula - Darcy formula
- Veisbahs:
 .
.
Express
šajā formulā ātrums V
caur plūsmu Q
no attiecības
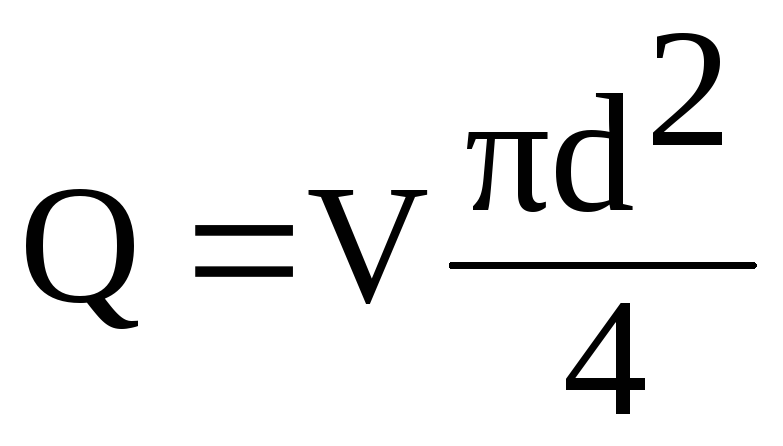
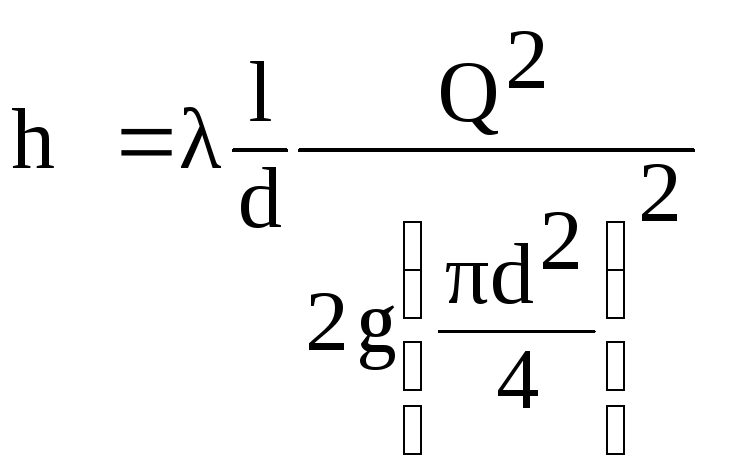
(6.1)
Priekš
noteikta diametra cauruļvads
daudzumu komplekss
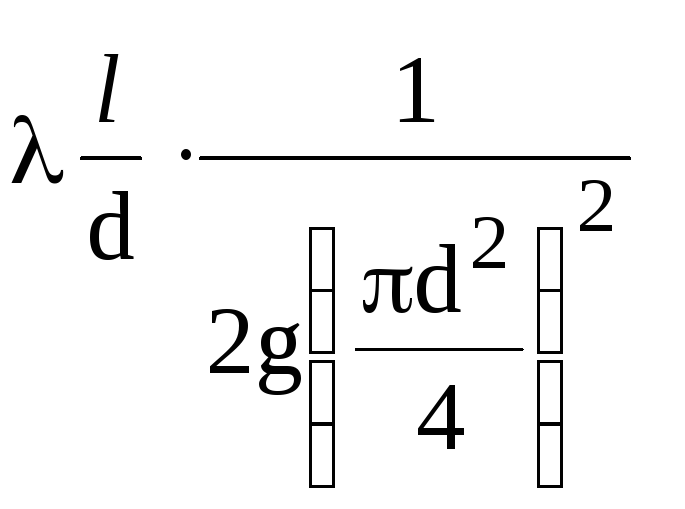
konstante (1/K2),
izņemot hidraulisko koeficientu
berze λ. Pamatojoties uz koncepciju
vidējais ekonomiskais ātrums Vs.e
parādīsim, ka norādītais koeficients λ
var attiecināt uz šo kompleksu, jo v
Šajā gadījumā Reinoldsa numurs būs
ir īpaša nozīme:
 ,
,
un Nikuradzes gabalā koeficients λ in
šai lietai būs konkrēts
nozīmē.
Pamatot
koncepcijas ieviešanas leģitimitāti
vidējo ekonomisko ātrumu šādi
argumentācija.
hidrauliskais
sistēma, piemēram, santehnika,
jūs varat izlaist noteiktus izdevumus
izgatavoti no dažāda diametra caurulēm. Plkst
Tajā pašā laikā, palielinoties diametram d,
tāpēc ātruma V samazināšanās
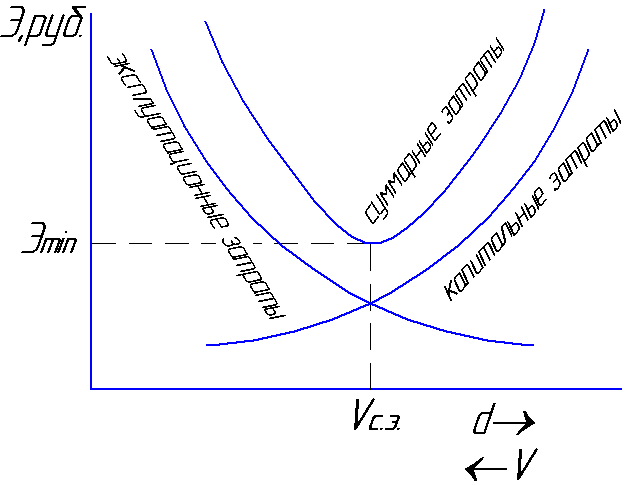
pieaugs kapitālie izdevumi, un
darbības izmaksas būs
samazinājums hidraulikas samazināšanās dēļ
zaudējumiem. Ātrums, kādā kopējais
izmaksas būs minimālas
tiks saukts par vidējo ekonomisko
ātrums Vs.e
= 0,8 ... 1,3 m / s (6.1. att.).
att.6.1
Tad
lineāro zudumu formula (6.1) iegūst formu
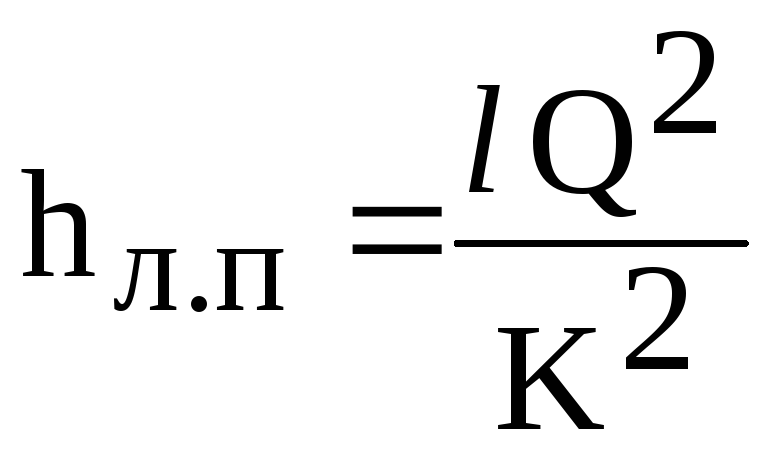
(6.2)
kur
K - cauruļvadam raksturīga plūsma
(plūsmas modulis), atkarībā no materiāla
cauruļvads, diametrs un plūsma. tiek ņemts
no tabulām.
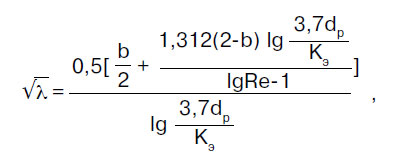
 ),C
),C ,
,