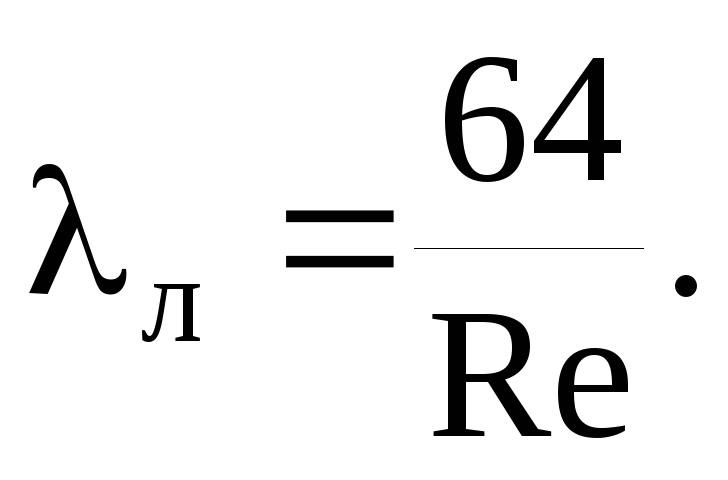1. Hydrostatische druk:
Hydrostatische druk is
interne drukkracht door:
door de werking van externe krachten die worden uitgeoefend op
bepaald punt in de vloeistof. zo'n druk
in alle richtingen is hetzelfde en hangt af
op de positie van een punt in een vloeistof in rust.
Afmeting van hydrostatische druk:
in het MKGSS systeem - kg/cm2 of t/m2,
in het SI-systeem - N/m2.
Basiseenheidsverhoudingen
druk:
|
kg/cm2 |
N/m2 |
|
|
technische sfeer |
1 |
98066,5 |
|
millimeter waterkolom |
0,0001 |
9,80665 |
|
millimeter kwik |
0,00136 |
133,32 |
In praktische berekeningen, 1 technisch
atmosfeer \u003d 1 kg / cm2 \u003d 10 m water. Kunst. =
735 mmHg Kunst. = 98070 N/m2.
Voor een onsamendrukbare vloeistof is dat:
in balans onder kracht
zwaartekracht, volledig hydrostatisch
punt druk:
p=p+

waarbij p de druk is op de vrije
vloeibaar oppervlak;

hoogte h met oppervlakte
doorsnede gelijk aan één;
h - onderdompelingsdiepte
punten;

Voor sommige vloeistoffen zijn de waarden
soortelijk gewicht gebruikt bij het oplossen
taken worden gegeven in de bijlage (tab.
P-3).
De waarde van overdruk over
atmosferisch (peen)
genaamd manometrische, of
overdruk:

Als de druk op het vrije oppervlak
gelijk aan atmosferisch, dan overmaat
druk pm=

Onder-atmosferische druk
de hoeveelheid wordt het vacuüm genoemd:
Rgek= peen- R.
De oplossing voor de meeste problemen hiervan
sectie is gerelateerd aan het gebruik
de basisvergelijking van hydrostatica

waarbij z de coördinaat is of
punt merk.
1. Algemene informatie over de hydraulische berekening van pijpleidingen
bij het berekenen
pijpleidingen die worden overwogen
constante, uniforme druk
beweging van een vloeistof
turbulent regime, in rondcilindrische
pijpen. Vloeistof in drukleidingen
staat onder druk en
hun doorsneden zijn volledig
gevuld. De beweging van vloeistof langs
pijpleiding ontstaat als gevolg
het feit dat de druk aan het begin ervan groter is dan
uiteindelijk.
hydraulisch
de berekening is gemaakt om te bepalen:
pijpleiding diameter: D
met een bekende
lengte om ervoor te zorgen overslaan
een bepaald debiet Q
of oprichting
bij een gegeven diameter en lengte van de vereiste
druk en vloeistofstroom. pijpleidingen
afhankelijk van de lengte en het patroon van hun
locaties zijn onderverdeeld in eenvoudige
en ingewikkeld. Naar eenvoudige pijpleidingen
omvat pijpleidingen die geen
takken over de lengte, met een constante
dezelfde uitgave.
pijpleidingen
bestaan uit buizen van dezelfde diameter
over de gehele lengte of uit secties van buizen van verschillende
diameters en lengtes. laatste geval
verwijst naar een seriële verbinding.
Eenvoudige pijpleidingen
afhankelijk van de lengte met een plot van local
weerstanden zijn onderverdeeld in korte en
lang. kort
pijpleidingen
zijn
pijpleidingen met een voldoende korte lengte,
waarin lokale weerstand
maken meer dan 10% van hydraulisch uit
lengte verlies. Ze omvatten bijvoorbeeld:
sifonbuizen, afzuiging
leidingen van schottenpompen, sifons (druk
waterleidingen onder het wegdek),
pijpleidingen in gebouwen en constructies
enzovoort.
lang
pijpleidingen
genaamd
pijpleidingen zijn relatief groot
lengtes waarin het hoofdverlies langs de lengte
aanzienlijk groter dan lokaal
verliezen. Lokale verliezen zijn
minder dan 5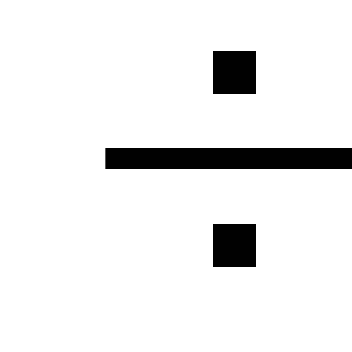
verliezen langs de lengte van de pijpleiding, en daarom
ze kunnen worden verwaarloosd of geïntroduceerd bij
hydraulische berekeningen toenemen
coëfficiënt gelijk aan 1.05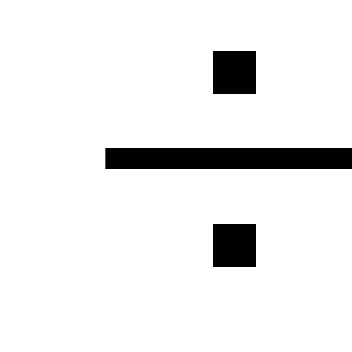
Lange pijpleidingen komen het systeem binnen
watervoorzieningsnetwerken, pompleidingen
stations, leidingen en pijpleidingen
industriële ondernemingen en
agrarische doeleinden en
enzovoort.
Complexe pijpleidingen
hebben verschillende takken over de lengte,
die. pijpleiding bestaat uit een netwerk van leidingen
bepaalde diameters en lengtes. Complex
pijpleidingen zijn onderverdeeld in:
parallel, doodlopend (vertakt),
ring (gesloten) pijpleidingen,
opgenomen in het waterleidingnet.
hydraulisch
pijpleidingberekening wordt gereduceerd als
meestal om drie hoofdproblemen op te lossen:
-
definitie
pijpleidingstroom Q,
indien gekend
druk H,
lengte ik
en diameter D
pijpleiding,
gezien de beschikbaarheid van bepaalde lokale
weerstanden of in hun afwezigheid; -
definitie
vereiste druk H,
nodig om een pas te beveiligen
bekende stroom Q
per pijpleiding
lang ik
en diameter D; -
definitie
pijpleiding diameter: D
wanneer
bekende hoofdwaarden H,
kosten Q
en lengte ik.
Het vloeistofdebiet is:
waarbij q > ontwerp vloeistofstroom, m3/s;
- oppervlakte van het live-gedeelte van de pijp, m2.
Wrijvingsweerstandscoëfficiënt λ wordt bepaald in overeenstemming met de voorschriften van de set regels SP 40-102-2000 "Ontwerp en installatie van pijpleidingen voor watervoorziening en rioleringssystemen gemaakt van polymere materialen. Algemene vereisten":
waarbij b een soortgelijk aantal vloeistofstroomregimes is; voor b > 2 wordt b = 2 genomen.
waarbij Re het werkelijke Reynoldsgetal is.
waarbij ν de kinematische viscositeitscoëfficiënt van de vloeistof is, m²/s. Bij het berekenen van koudwaterleidingen wordt aangenomen dat deze gelijk is aan 1,31 10-6 m² / s - de viscositeit van water bij een temperatuur van +10 ° C;
Rekv > - Reynoldsgetal dat overeenkomt met het begin van het kwadratische gebied van hydraulische weerstand.
waarbij Ke de hydraulische ruwheid van het buismateriaal is, m. Voor buizen gemaakt van polymeermaterialen wordt Ke = 0.00002 m genomen als de buisfabrikant geen andere ruwheidswaarden geeft.
In die gevallen waarin Re ≥ Rekv vloeit, wordt de berekende waarde van de parameter b gelijk aan 2 en wordt formule (4) aanzienlijk vereenvoudigd, waardoor het de bekende Prandtl-formule wordt:
Bij Ke = 0,00002 m treedt het kwadratische weerstandsgebied op bij een waterdebiet (ν = 1,31 10-6 m²/s) gelijk aan 32,75 m/s, wat praktisch onbereikbaar is in openbare waterleidingsystemen.
Voor alledaagse berekeningen worden nomogrammen aanbevolen en voor nauwkeurigere berekeningen - "Tabellen voor hydraulische berekeningen van pijpleidingen gemaakt van polymere materialen", volume 1 "Drukleidingen" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
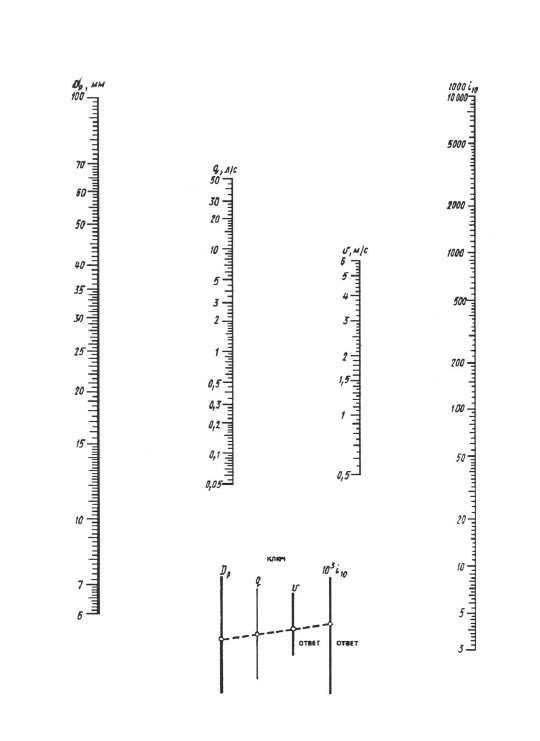
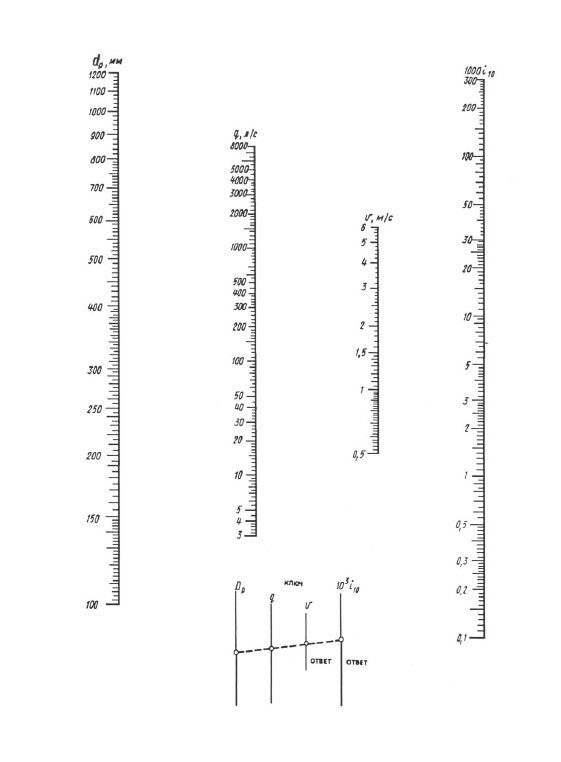
Bij het berekenen volgens nomogrammen wordt het resultaat bereikt door één overlay van de liniaal - u moet het punt verbinden met de waarde van de berekende diameter op de dp-schaal met het punt met de waarde van het berekende debiet op de q (l / s) schaal met een rechte lijn, zet deze rechte lijn voort totdat deze de schalen van snelheid V en specifieke verliezen opvoerhoogte 1000 i (mm/m) kruist. De snijpunten van een rechte lijn met deze schalen geven de waarde V en 1000 i.
Zoals u weet, zijn de kosten van elektriciteit voor het verpompen van vloeistof recht evenredig met de waarde van H (ceteris paribus). Door de uitdrukking ( 3 ) in de formule ( 2 ) in te vullen, is het gemakkelijk in te zien dat de waarde van i (en bijgevolg H) omgekeerd evenredig is met de berekende diameter dp tot de vijfde graad.
Hierboven is aangetoond dat de waarde van dp afhangt van de dikte van de buiswand e: hoe dunner de wand, hoe hoger dp en dus hoe lager het drukverlies door wrijving en de kosten van elektriciteit.
Als de MRS-waarde van de leiding om welke reden dan ook verandert, moeten de diameter en wanddikte (SDR) opnieuw worden berekend.
Houd er rekening mee dat in een aantal gevallen het gebruik van buizen met MRS 10 in plaats van buizen met MRS 8, vooral buizen met MRS 6.3, het mogelijk maakt om de diameter van de pijpleiding met één maat te verkleinen. Daarom maakt het gebruik van polyethyleen PE 80 (MRS 8) en PE 100 (MRS 10) in plaats van polyethyleen PE 63 (MRS 6.3) in onze tijd niet alleen de wanddikte van buizen, hun gewicht en materiaalverbruik, maar ook om de energiekosten voor het verpompen van vloeistof te verlagen (ceteris paribus).
In de afgelopen jaren (na 2013) zijn buizen van PE80 polyethyleen vrijwel volledig uit productie vervangen door buizen van PE100 kwaliteit polyethyleen. Dit wordt verklaard door het feit dat de grondstoffen waaruit de buizen zijn gemaakt met het merk PE100 uit het buitenland worden aangevoerd.En ook door het feit dat polyethyleen 100-kwaliteit meer sterkte-eigenschappen heeft, waardoor buizen worden geproduceerd met dezelfde eigenschappen als buizen gemaakt van PE80, maar met een dunnere wand, waardoor de doorvoer van polyethyleen pijpleidingen toeneemt.
Nomogram voor het bepalen van drukverliezen in leidingen met een diameter van 6, 100 mm.
Nomogram voor het bepalen van drukverliezen in leidingen met een diameter van 100, 1200 mm.
Reynolds-criterium
Deze afhankelijkheid werd naar voren gebracht door de Engelse natuurkundige en ingenieur Osborne Reynolds (1842-1912).
Het criterium dat helpt bij het beantwoorden van de vraag of viscositeit moet worden overwogen, is het Reynolds-getal Re. Het is gelijk aan de verhouding van de bewegingsenergie van een element van een stromende vloeistof tot het werk van interne wrijvingskrachten.
Beschouw een kubisch vloeistofelement met randlengte n. De kinetische energie van een element is:
Volgens de wet van Newton wordt de wrijvingskracht die op een vloeibaar element werkt als volgt gedefinieerd:
De arbeid van deze kracht bij het verplaatsen van een vloeibaar element over een afstand n is
en de verhouding van de kinetische energie van het vloeibare element tot de arbeid van de wrijvingskracht is
We verminderen en krijgen:
Re wordt het Reynoldsgetal genoemd.
Re is dus een dimensieloze grootheid die de relatieve rol van viskeuze krachten kenmerkt.
Als bijvoorbeeld de afmetingen van het lichaam waarmee de vloeistof of het gas in contact is erg klein zijn, dan zal Re zelfs bij een lage viscositeit onbeduidend zijn en zullen wrijvingskrachten een overheersende rol spelen. Integendeel, als de afmetingen van het lichaam en de snelheid groot zijn, dan hebben Re >> 1 en zelfs een grote viscositeit bijna geen effect op de aard van de beweging.
Niet altijd grote Reynolds-getallen betekenen echter dat viscositeit geen rol speelt. Dus wanneer een zeer grote (enkele tien- of honderdduizenden) waarde van het Re-getal wordt bereikt, verandert een gladde laminaire (van het Latijnse lamina - "plaat") stroming in een turbulente (van het Latijnse turbulentus - "stormachtig" , “chaotisch”), vergezeld van chaotische, onvaste bewegingen van vloeistoffen. Dit effect is te zien als je een waterkraan langzaam opendraait: een dun straaltje stroomt meestal soepel, maar bij een toename van de snelheid van het water wordt de gladheid van de stroming verstoord. In een straal die onder hoge druk naar buiten stroomt, bewegen vloeibare deeltjes willekeurig, oscillerend, alle bewegingen gaan gepaard met sterke vermenging.
Het optreden van turbulentie verhoogt de weerstand aanzienlijk. In een pijpleiding is de turbulente stroomsnelheid kleiner dan de laminaire stroomsnelheid bij dezelfde drukval. Maar turbulentie is niet altijd slecht. Doordat menging tijdens turbulentie zeer belangrijk is, vindt warmteoverdracht - koeling of verwarming van toeslagstoffen - veel intensiever plaats; chemische reacties verspreiden zich sneller.
Bernoulli's vergelijking van stationaire beweging
Een van de belangrijkste vergelijkingen van de hydromechanica werd in 1738 verkregen door de Zwitserse wetenschapper Daniel Bernoulli (1700-1782). Hij slaagde er voor het eerst in om de beweging van een ideale vloeistof te beschrijven, uitgedrukt in de Bernoulli-formule.
Een ideale vloeistof is een vloeistof waarin er geen wrijvingskrachten zijn tussen de elementen van een ideale vloeistof, en ook niet tussen de ideale vloeistof en de wanden van het vat.
De vergelijking van stationaire beweging die zijn naam draagt is:
waarbij P de druk van de vloeistof is, ρ de dichtheid is, v de bewegingssnelheid is, g de versnelling van de vrije val is, h de hoogte is waarop het element van de vloeistof zich bevindt.
De betekenis van de Bernoulli-vergelijking is dat binnen een systeem gevuld met vloeistof (pijpleidingsectie) de totale energie van elk punt altijd onveranderd is.
De Bernoulli-vergelijking heeft drie termen:
- ρ⋅v2/2 - dynamische druk - kinetische energie per volume-eenheid van de aandrijfvloeistof;
- ρ⋅g⋅h - gewichtsdruk - potentiële energie van een eenheidsvolume vloeistof;
- P - statische druk, in zijn oorsprong is het werk van drukkrachten en vertegenwoordigt het geen reserve van een speciaal type energie ("drukenergie").
Deze vergelijking verklaart waarom in smalle delen van de leiding de stroomsnelheid toeneemt en de druk op de leidingwanden afneemt. De maximale druk in de leidingen wordt precies ingesteld op de plaats waar de leiding de grootste doorsnede heeft. Smalle delen van de leiding zijn in dit opzicht veilig, maar de druk daarin kan zo sterk dalen dat de vloeistof gaat koken, wat kan leiden tot cavitatie en vernietiging van het leidingmateriaal.
Navier-Stokes-vergelijking voor viskeuze vloeistoffen
In een meer rigoureuze formulering wordt de lineaire afhankelijkheid van viskeuze wrijving van de verandering in vloeistofsnelheid de Navier-Stokes-vergelijking genoemd. Het houdt rekening met de samendrukbaarheid van vloeistoffen en gassen en is, in tegenstelling tot de wet van Newton, niet alleen geldig nabij het oppervlak van een vast lichaam, maar ook op elk punt in de vloeistof (dichtbij het oppervlak van een vast lichaam in het geval van een onsamendrukbare vloeistof vallen de Navier-Stokes-vergelijking en de wet van Newton samen).
Alle gassen waarvoor aan de voorwaarde van een continu medium wordt voldaan, voldoen ook aan de Navier-Stokes-vergelijking, d.w.z. zijn Newtoniaanse vloeistoffen.
De viscositeit van vloeistoffen en gassen is meestal significant bij relatief lage snelheden, daarom wordt soms gezegd dat Euler-hydrodynamica een speciaal (beperkend) geval is van hoge snelheden van Navier-Stokes-hydrodynamica.
Bij lage snelheden, in overeenstemming met de wet van viskeuze wrijving van Newton, is de weerstandskracht van het lichaam evenredig met de snelheid. Bij hoge snelheden, wanneer de viscositeit niet langer een belangrijke rol speelt, is de weerstand van het lichaam evenredig met het kwadraat van de snelheid (wat voor het eerst werd ontdekt en onderbouwd door Newton).
Hydraulische berekeningsvolgorde
1.
De hoofdcirculatie is geselecteerd
ringverwarmingssysteem (meeste
ongunstig gelegen in de hydraulische
relatie). In doodlopende tweepijps
systemen is een ring die doorgaat
lagere instrument van de meest afgelegen en
belaste stijgleiding, in enkelpijps -
via de meest afgelegen en geladen
stijger.
Bijvoorbeeld,
in een tweepijpsverwarmingssysteem met
bovenste bedrading hoofdcirculatie
de ring zal passeren van het hittepunt
via de hoofdstijgleiding, toevoerleiding,
via de meest afgelegen stijgleiding, verwarming
beneden toestel, retourleiding
naar het verwarmingspunt.
V
systemen met bijbehorende waterbeweging in
de ring wordt als de belangrijkste genomen,
het meest door het midden gaan
geladen staan.
2.
De hoofdcirculatiering breekt
in percelen (de plot wordt gekenmerkt
constante waterstroom en hetzelfde
diameter). Het diagram toont:
sectienummers, hun lengtes en thermische
ladingen. Thermische belasting van hoofd
plots wordt bepaald door optellen
thermische belastingen bediend door deze
percelen. Om pijpdiameter te selecteren:
er worden twee hoeveelheden gebruikt:
een)
gegeven waterstroom;
B)
geschatte specifieke drukverliezen
voor wrijving in de ontwerpcirculatie
ring Rwo.
Voor
berekening Rcp
moet de lengte van de belangrijkste weten
circulatiering en berekend
circulatie druk.
3.
De berekende oplage
formule druk
 ,
,
(5.1)
waar
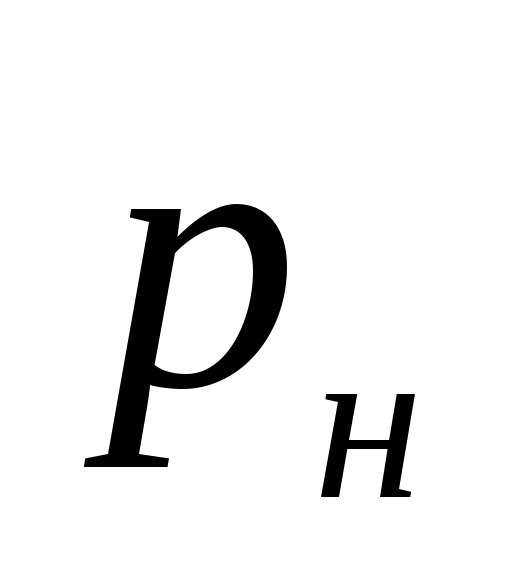
druk gecreëerd door de pomp, Pa.
Systeemontwerppraktijk
verwarming toonde aan dat de meeste
het is raadzaam om de druk van de pomp op te nemen,
Gelijk
 ,
,
(5.2)
waar
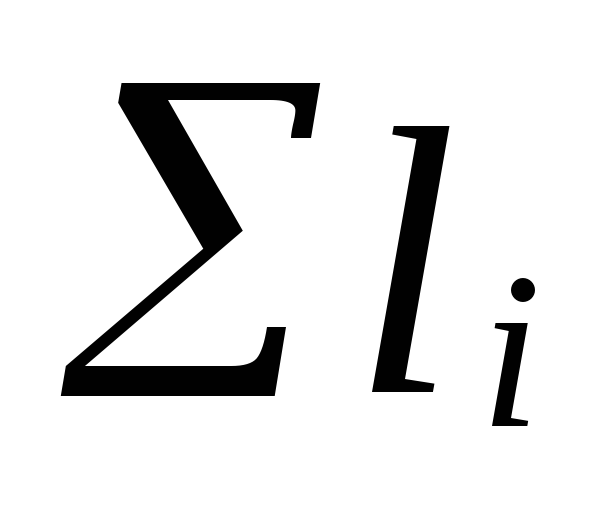
de som van de lengtes van de secties van de hoofdcirculatie
ringen;
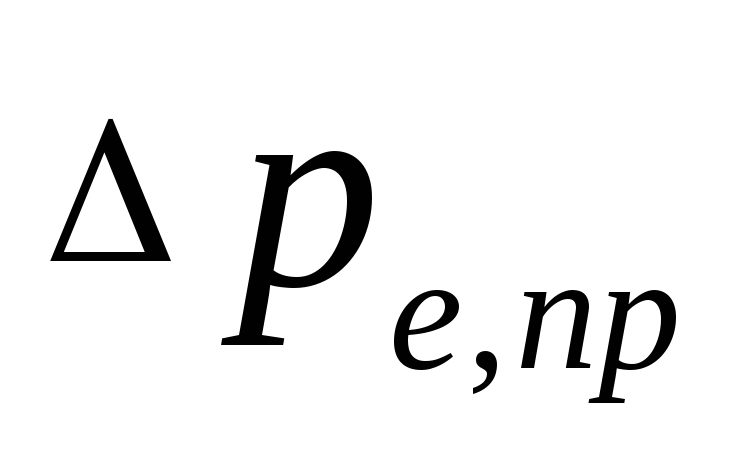
natuurlijke druk die optreedt wanneer
waterkoeling in toestellen, Pa, mogelijk
bepalen hoe
 ,
,
(5.3)
waar
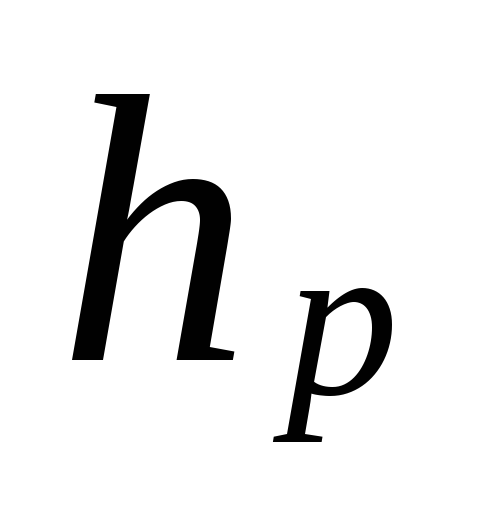
afstand van het midden van de pomp (lift)
naar het midden van het apparaat van de benedenverdieping, m.
Betekenis
coëfficiënt mogelijk
bepalen uit tabel 5.1.
tafel
5.1 - Betekenis c
afhankelijk van de ontwerptemperatuur
water in het verwarmingssysteem
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
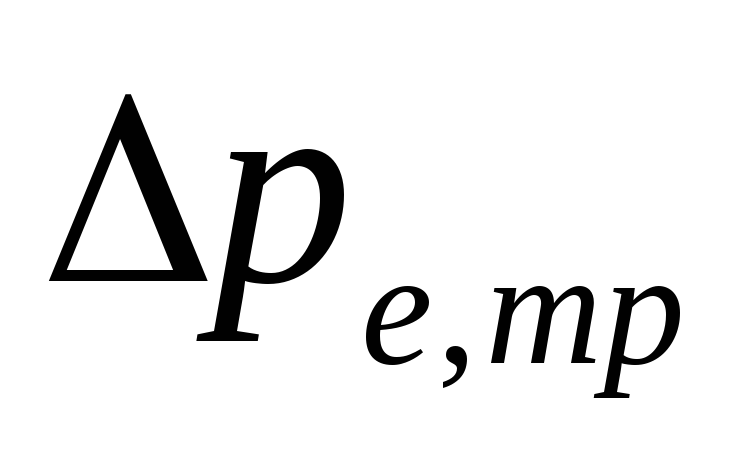
natuurlijke druk in
als gevolg van waterkoeling in leidingen
.
V
pompsystemen met bodembedrading
grootte
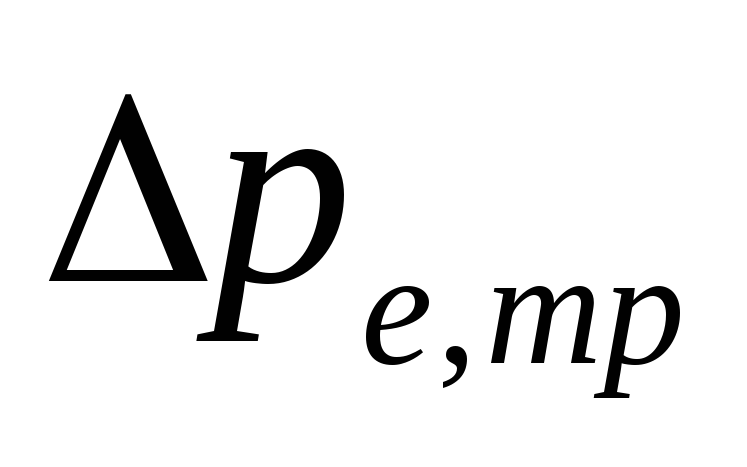
-
Worden bepaald
specifiek wrijvingsdrukverlies
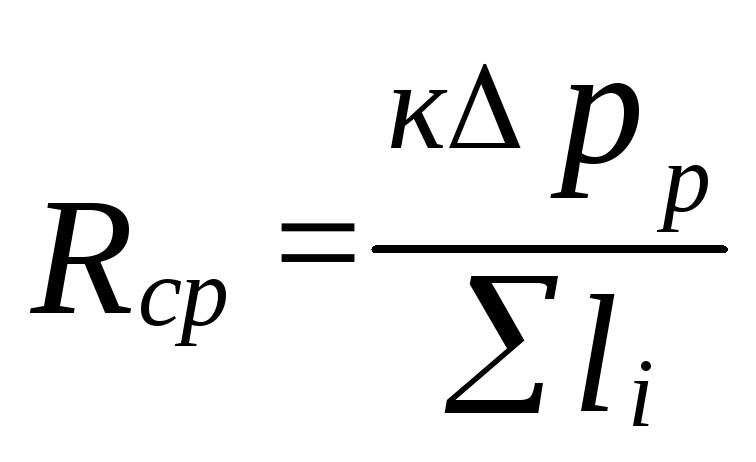
(5.4)
waar
k=0,65 bepaalt het aandeel drukverliezen
voor wrijving.
5.
De waterstroom in het gebied wordt bepaald door:
formule
 (5.5)
(5.5)
waar
Q
- warmtebelasting op de site, W:
(tG
- tO)
- temperatuurverschil van de koelvloeistof.
6.
op grootte
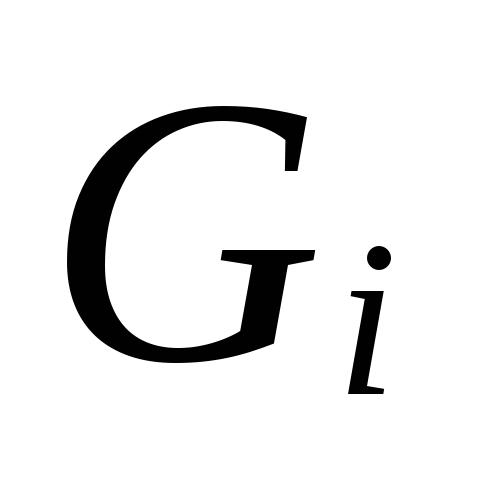
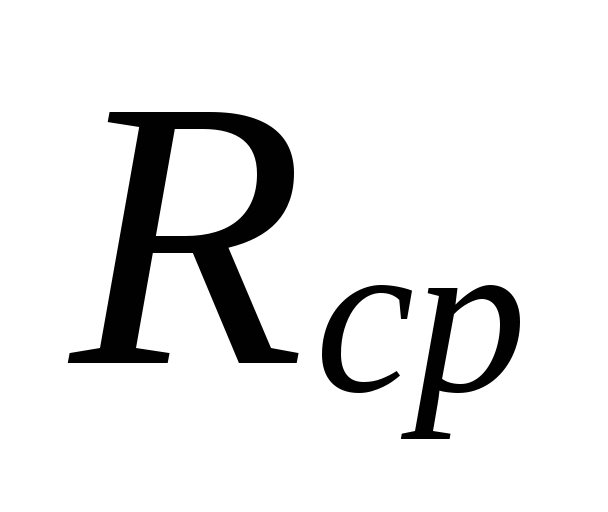
.

6.
Voor geselecteerde pijpleidingdiameters
en het geschatte waterverbruik wordt bepaald
koelvloeistof snelheid v
en de werkelijke specifieke
wrijving drukverlies RF.
Bij
selectie van diameters in gebieden met kleine
koelmiddelstroomsnelheden kunnen zijn:
grote verschillen tussen
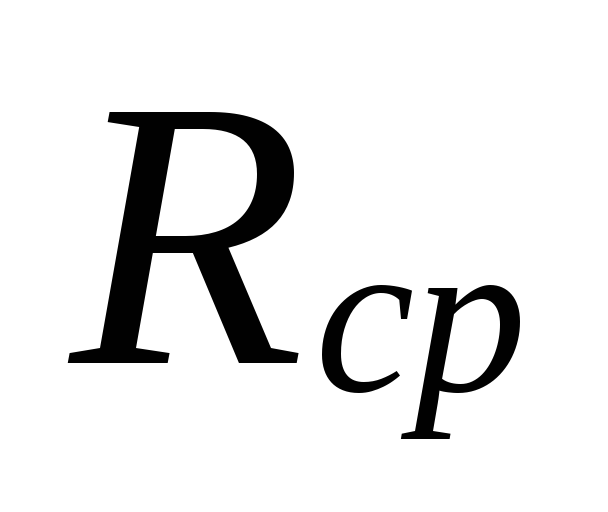
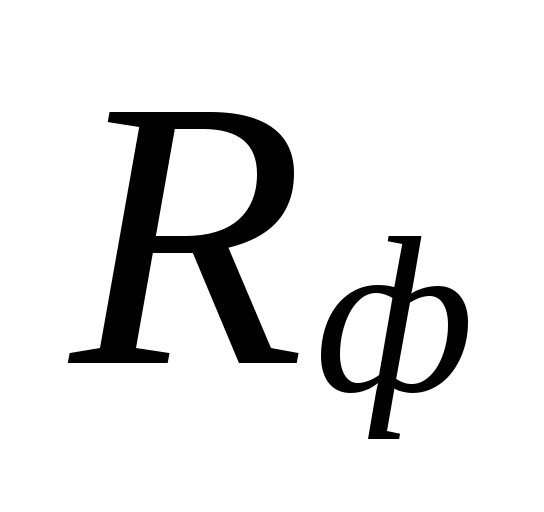
onderschatte verliezen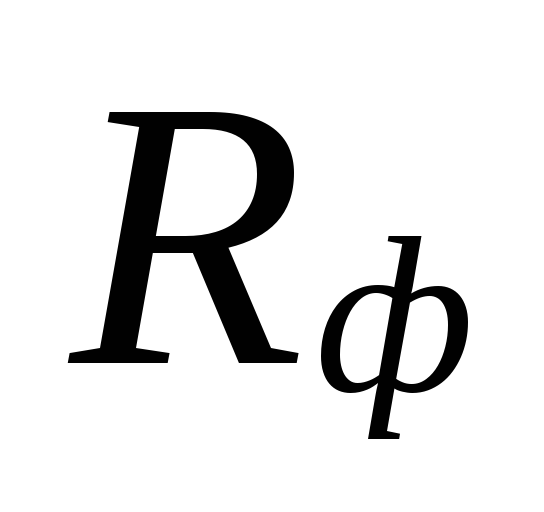
deze gebieden worden gecompenseerd door een overschatting
hoeveelheden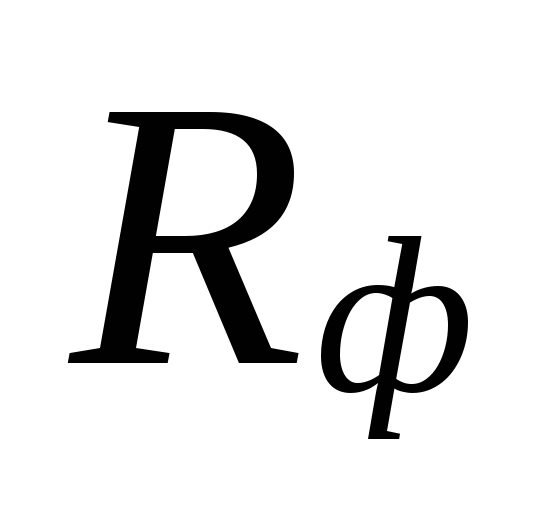
7.
Wrijvingsdrukverliezen worden bepaald
op het berekende gebied, Pa:
 .
.
(5.6)
resultaten
berekeningen zijn opgenomen in Tabel 5.2.
8.
Drukverliezen in lokaal
weerstanden met behulp van de formule:
 ,
,
(5.7)
waar
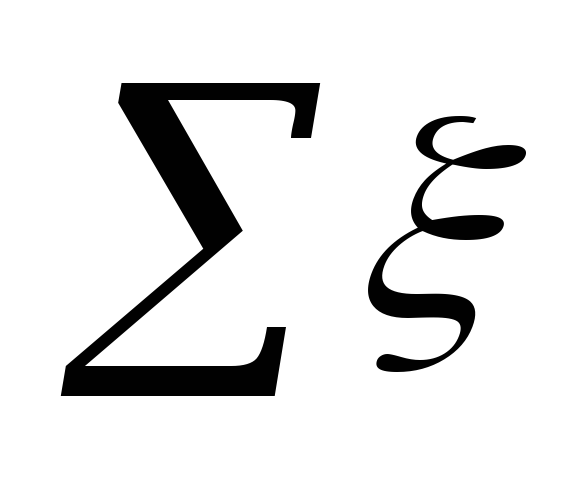
in het vestigingsgebied.
Betekenis ξ
op elke site zijn samengevat in de tabel. 5.3.
Tabel 5.3 -
Lokale weerstandscoëfficiënten
|
nr. p / p |
namen |
Waarden |
Opmerkingen: |
9.
Bepaal het totale drukverlies
op elk gebied
 .
.
(5.8)
10. Bepaal
totaal drukverlies door wrijving en
in lokale weerstanden in het algemeen
circulatie ring
 .
.
(5.9)
11. Vergelijk p
Met pR.
Totaal drukverlies over de ring
moet kleiner zijn dan pR
op de
 .
.
(5.10)
voorraad wegwerpartikelen
druk is nodig op onverklaarde in
berekening van hydraulische weerstand.
Als de voorwaarden niet zijn
worden uitgevoerd, is het op sommige
delen van de ring om de diameters van de leidingen te wijzigen.
12. Na berekening
hoofdcirculatiering
maak de koppeling van de resterende ringen. V
alleen elke nieuwe ring telt
extra niet-gemeenschappelijke ruimtes,
parallel geschakeld met secties
hoofdring.
Verlies discrepantie
drukken op parallel aangesloten
percelen toegestaan tot 15% met een doodlopende weg
de beweging van water en tot 5% - bij het passeren.
tafel
5.2 - Resultaten van hydraulische berekening
voor verwarmingssysteem:
|
Op de |
Door |
Door |
||||||||||||||
|
Nummer |
thermisch |
Consumptie |
Lengte |
Diameter |
Snelheid |
Specifiek |
Verliezen |
Som |
Verliezen |
D, |
v, |
R, |
ptr, |
∑ξ |
Z, |
Rl+Z, |
Les 6
Verandering in gastemperatuur langs de lengte van de gasleiding
In stationaire gasstroom, de massa
het debiet in de gasleiding is
 . (2.41)
. (2.41)
In feite is de beweging van gas in de gaspijpleiding
is altijd niet-isotherm. V
Tijdens compressie warmt het gas op.
Zelfs na afkoeling bij de COP, is de temperatuur
gas dat de pijpleiding binnenkomt
is ongeveer 2040С,
die veel hoger is dan de temperatuur
omgeving (T).
In de praktijk wordt de temperatuur van het gas
dicht bij omgevingstemperatuur
alleen voor gasleidingen met een kleine diameter
(Dy0.
Bovendien moet er rekening mee worden gehouden dat
pijpleiding gas
is een echt gas, wat inherent is
het Joule-Thompson-effect, dat rekening houdt met
absorptie van warmte tijdens gasexpansie.
Wanneer de temperatuur over de lengte verandert
gasleiding gasbeweging wordt beschreven:
stelsel vergelijkingen:
specifieke energie ,
,
continuïteit ,
,
staten ,
,
warmte balans .
.
Beschouw in de eerste benadering de vergelijking
warmtebalans zonder rekening te houden met het effect
Joule Thompson. De vergelijking integreren
warmte balans
 ,
,
we krijgen
 , (2.42)
, (2.42)
waar ;
;
KSR- gemiddeld op de site vol
warmteoverdrachtscoëfficiënt van gas naar
omgeving;
G is de massastroomsnelheid van gas;
CP–
gemiddelde isobare warmtecapaciteit van het gas.
een waardetL wordt het dimensieloze criterium genoemd
Shukhov
 (2.43)
(2.43)
Dus de gastemperatuur aan het einde
gasleiding zal worden
 . (2.44)
. (2.44)
Op afstand x vanaf het begin
gasleiding gastemperatuur wordt bepaald
volgens de formule
 . (2.45)
. (2.45)
Verandering in temperatuur langs de lengte van de gasleiding
exponentieel is (afb.
2.6).
Overwegen
effect van verandering van de gastemperatuur op
prestaties van de pijpleiding.
Beide zijden van de specifieke vergelijking vermenigvuldigen
energie op 2 en uiting ,
,
we krijgen
 . (2.46)
. (2.46)
We drukken de dichtheid van het gas aan de linkerkant uit
uitdrukkingen (2.46) uit de toestandsvergelijking
 ,
,
product (uit de continuïteitsvergelijking)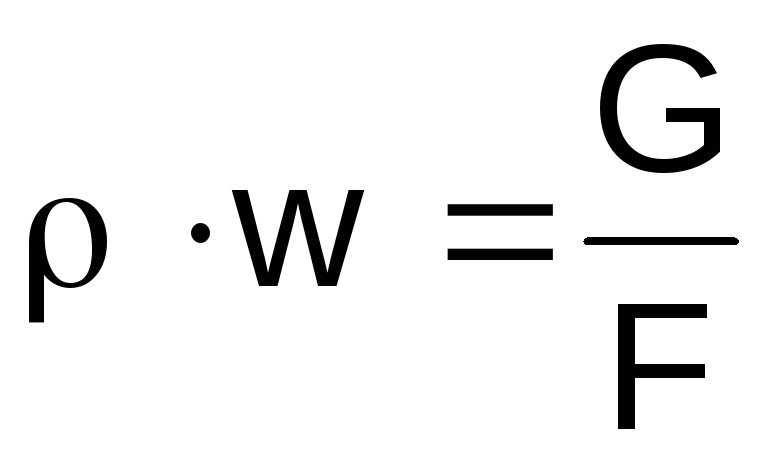
evenwicht .
.
Met dit in gedachten, de specifieke vergelijking
energie neemt de vorm aan
 (2.47)
(2.47)
of
 . (2.48)
. (2.48)
aanduiding
 en het integreren van de linkerkant van de vergelijking
en het integreren van de linkerkant van de vergelijking
(2,48) van PHdoPNAAR, en rechts van THpuntNAAR, we krijgen
 . (2.49)
. (2.49)
door te vervangen
 , (2.50)
, (2.50)
we hebben
 . (2.51)
. (2.51)
Na integratie in de opgegeven
limieten, we krijgen

 . (2.52)
. (2.52)
Rekening houdend met (2.42)

of
 , (2.53)
, (2.53)
waar is een correctiefactor die rekening houdt met
is een correctiefactor die rekening houdt met
temperatuurverandering langs de lengte van de gasleiding
(niet-isothermaliteit van de gasstroom).
Rekening houdend met (2.53), de afhankelijkheid voor het bepalen van
massastroomsnelheid van gas zal de vorm aannemen:
 . (2.54)
. (2.54)
WaardeHaltijd groter dan één, dus
massastroom van gas bij het veranderen:
temperatuur langs de lengte van de gasleiding
(niet-isotherm stromingsregime) altijd
minder dan in isotherme modus
(T=idem). Product THheet de gemiddelde integraal
temperatuur van het gas in de pijpleiding.
Met de waarden van het Shukhov-nummer Shu4
gasstroom in de pijpleiding
beschouw bijna isotherm
bij T=idem. Zo'n temperatuur
modus is mogelijk bij het pompen van gas met
lage gasleidingskosten
kleine (minder dan 500 mm) diameter tot een significante
afstand.
Effect van veranderende gastemperatuur
manifesteert zich voor de waarden van het Shukhov-nummer
Shu
Bij
gas pompen de aanwezigheid van een gashendel
effect leidt tot een diepere
gaskoeling dan alleen met warmtewisseling
met grond. In dit geval is de temperatuur
gas kan zelfs tot onder dalen
temperatuur T (afb.
2.7).
Rijst. 2.7. Invloed van het Joule-Thompson-effect
op de gastemperatuurverdeling over
pijpleiding lengte:
1 - zonder rekening te houden met Di; 2 - met
rekening houdend met Di
Dan, rekening houdend met de Joule-Thompson-coëfficiënt
wet van temperatuurverandering langs de lengte
neemt de vorm aan
 , (2.55)
, (2.55)
5 Hydraulische verliezen
Verschil
oliedruk in twee delen van één
en dezelfde pijpleiding, op voorwaarde dat:
de eerste bevindt zich stroomopwaarts, en
de tweede - hieronder, wordt bepaald vergelijking
Bernoulli
 ,
,
waar
H2
- H1
- het hoogteverschil van de zwaartepunten
secties van een willekeurig gekozen
horizontaal niveau;
v1,
v2
– gemiddelde snelheden van olie in secties;
g - krachtversnelling
zwaartekracht;

hydraulische verliezen tijdens beweging
oliën van het eerste deel naar het tweede.
De vergelijking
Bernoulli volop in gebruik
voor het berekenen van zuigleidingen van pompen;
in andere gevallen, de eerste termijn,
meestal verwaarloosd en overwogen:

hydraulisch
verliezen worden meestal onderverdeeld in lokale
verliezen en wrijvingsverliezen over de lengte
pijpleidingen (lineair).
1.5.1
lokale verliezen
energieën zijn te wijten aan lokale
hydraulische weerstand,
stromingsvervorming veroorzaken. lokaal
weerstanden zijn: vernauwingen,
uitbreiding, afronding van pijpleidingen,
filters, regelapparatuur en
regelgeving, enz. Tijdens het stromen
vloeistoffen door lokale weerstanden
de snelheid verandert en meestal zijn er
grote wervelingen.
Verliezen
druk van lokale weerstanden
bepaald door de formule Weisbach:
 MPa
MPa
(of
 Vader),
Vader),
waar

verlies,
v
is de gemiddelde stroomsnelheid over de dwarsdoorsnede
in een leiding achter lokale weerstand, m/s;
,
N/m3;
g=9,81 m/s2.
Elk
lokale weerstand wordt gekenmerkt
door zijn coëfficiëntwaarde

Bij turbulente stroming zijn de waarden
weerstand en verandert heel weinig
met een verandering in de grootte van de sectie, snelheid
vloeistofstroom en viscositeit. Dus
neem aan dat ze niet afhankelijk zijn van het aantal
Reynolds Re.
Waarden

bijvoorbeeld voor tees met dezelfde
kanaaldiameters worden gelijk genomen,
als:
stromen
optellen, uiteenlopen; stromen
passeren;









Bij
pijp bocht

Waarden

in hydraulische systemen van apparatuur, ontleend aan
referentie literatuur.
Bij
laminaire stroming (Re
Verliezen
druk van lokale weerstanden bij
laminaire stroming wordt bepaald door
formule:
 MPa
MPa
waar

= a

hoeveelheden
drukverlies in standaard
hydraulische apparaten voor
nominaal debiet meestal:
vermeld in hun technische specificaties.
1.5.2
verlies op
lengte wrijving
is het energieverlies dat optreedt
in rechte buizen met constante doorsnede,
die. met uniforme vloeistofstroom,
en toenemen in verhouding tot de lengte
pijpen. Deze verliezen zijn te wijten aan interne
wrijving in een vloeistof, en hebben daarom
plaats in zowel ruwe als gladde buizen.
Verliezen
pijpleiding wrijvingsdruk:
wordt bepaald door de formule Darcy:
 MPa
MPa
waar

ik
en doe
- lengte en binnendiameter van de pijpleiding,
mm.
Deze
de formule is zowel toepasbaar voor laminaire,
evenals in turbulente stroming; verschil
bestaat alleen uit de waarden van de coëfficiënt

Bij
laminaire stroming (Re
Bij
turbulente stromingscoëfficiënt van wrijving
is niet alleen een functie van Re, maar
hangt ook af van de ruwheid van de interne
pijp oppervlak. Voor hydraulisch
zacht pijpen,
die. met een ruwheid die
heeft praktisch geen invloed op de weerstand,
turbulente wrijvingscoëfficiënt
modus kan worden bepaald door de formule: pc.
Konakova:

pijp
wordt als hydraulisch soepel beschouwd als
(d/k)>(Re/20),
waarbij k de equivalente ruwheid is,
mm. Bijvoorbeeld voor nieuw naadloos staal
pijpen k≈0.03
mm, en na enkele jaren van gebruik
k≈0.2
mm, voor nieuwe naadloze buizen van
non-ferro metalen k≈0.005
mm. Deze buizen worden vaak gebruikt in
hydraulische systemen van werktuigmachines.
Coëfficiënt
wrijving in het turbulente regime kan zijn:
bepalen met formule Altshulya,
universeel zijn (d.w.z. toepasbaar)
in elk geval):

2. Stroomkarakteristieken van de pijpleidingstroommodule
Laat ons herdenken
lineaire verliesformule - Darcy-formule
-Weisbach:
 .
.
nadrukkelijk
in deze formule is de snelheid V
door stroom Q
van de verhouding
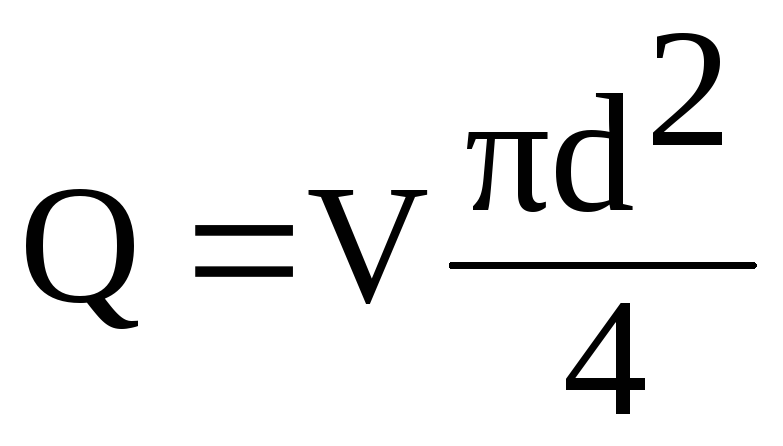
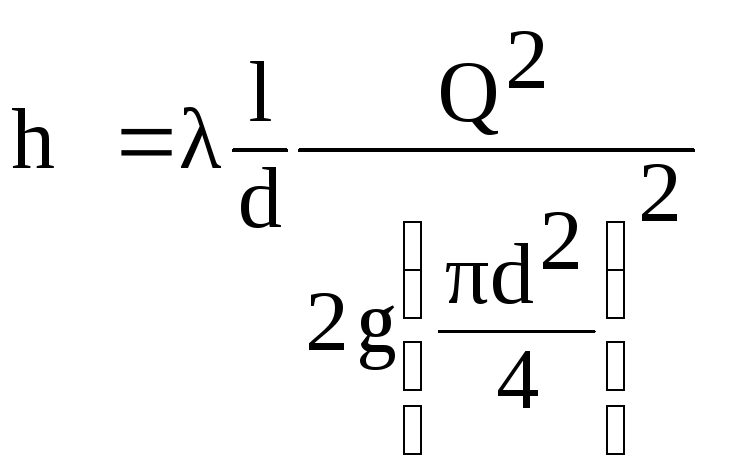
(6.1)
Voor
pijpleiding van een bepaalde diameter
complex van grootheden
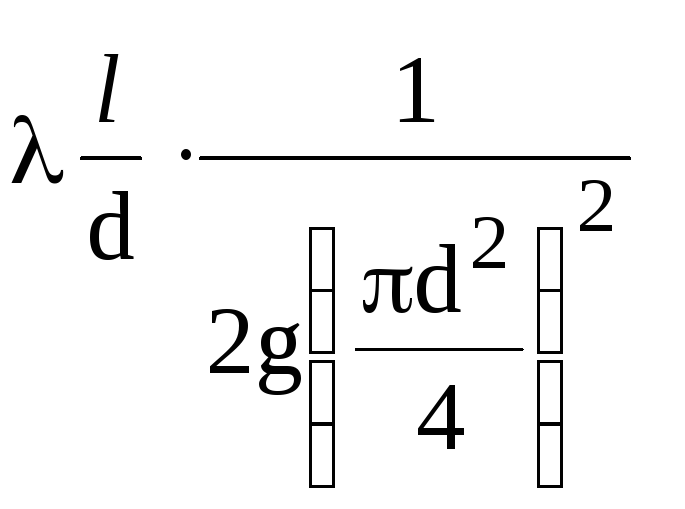
constante (1/K2),
behalve de hydraulische coëfficiënt
wrijving . Gebaseerd op het concept
gemiddelde economische snelheid Vs.e
laten we aantonen dat de aangegeven coëfficiënt λ
kan worden toegeschreven aan dit complex, omdat v
In dit geval is het Reynoldsgetal
een specifieke betekenis hebben:
 ,
,
en op de Nikuradze-plot, de coëfficiënt λ in
deze zaak heeft een specifieke
betekenis.
Verantwoorden
legitimiteit van de introductie van het concept
gemiddelde economische snelheid als volgt:
redenering.
hydraulisch
installaties, zoals sanitair,
u kunt een bepaalde uitgave overslaan
gemaakt van buizen met verschillende diameters. Bij
Tegelijkertijd, met een toename van de diameter d,
daarom een afname van de snelheid V
kapitaaluitgaven zullen stijgen, en
bedrijfskosten zullen
afname als gevolg van een afname in hydraulisch
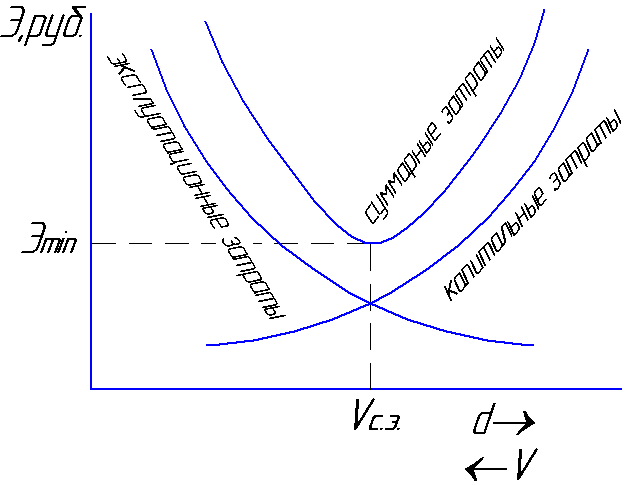
verliezen. De snelheid waarmee de totale
kosten zullen minimaal zijn
zal de gemiddelde economische worden genoemd
snelheid Vs.e
= 0,8 ... 1,3 m/s (afb. 6.1).
fig.6.1
Dan
de lineaire verliesformule (6.1) heeft de vorm
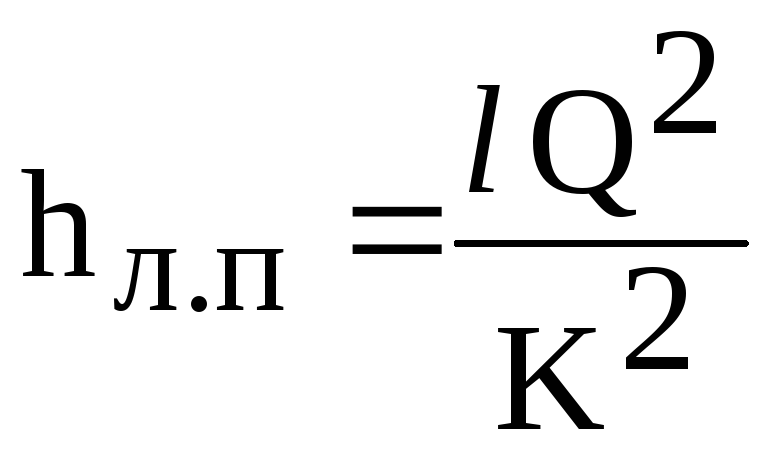
(6.2)
waar
K - stroomkarakteristiek van de pijpleiding
(stromingsmodulus), afhankelijk van materiaal
pijpleiding, diameter en stroom. is bezet
van tafels.
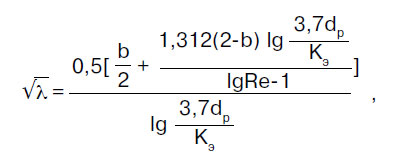
 ),C
),C ,
,