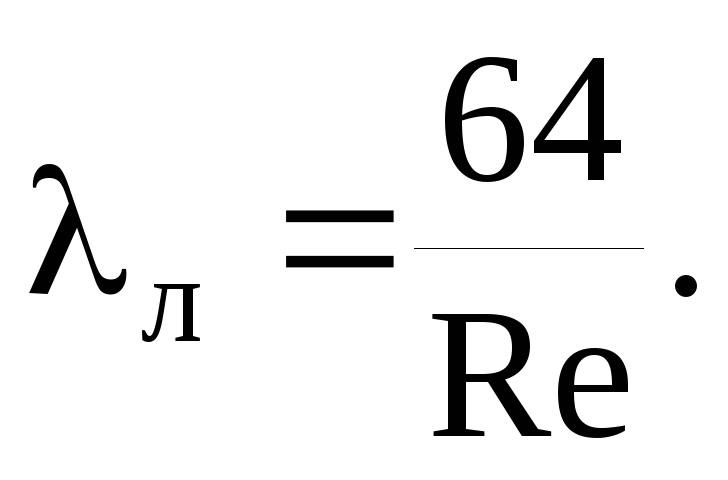1. Presiunea hidrostatică
Presiunea hidrostatică este
forța internă de compresiune datorată
prin acţiunea forţelor externe aplicate asupra
punct dat în fluid. O asemenea presiune
în toate direcțiile este același și depinde
asupra poziției unui punct dintr-un fluid în repaus.
Dimensiunea presiunii hidrostatice
în sistemul MKGSS - kg / cm2 sau t / m2,
în sistemul SI - N/m2.
Rapoartele unitare de bază
presiune:
|
kg/cm2 |
N/m2 |
|
|
atmosfera tehnica |
1 |
98066,5 |
|
milimetru de coloană de apă |
0,0001 |
9,80665 |
|
milimetru de mercur |
0,00136 |
133,32 |
În calcule practice, 1 tehnic
atmosferă \u003d 1 kg / cm2 \u003d 10 m apă. Artă. =
735 mmHg Artă. = 98070 N/m2.
Pentru un fluid incompresibil adică
în echilibru sub forţă
gravitație, complet hidrostatic
presiune punctuala:
p=p+

unde p este presiunea asupra liberului
suprafata lichida;

inaltime h cu suprafata
secțiune transversală egală cu unu;
h - adâncimea de scufundare
puncte;

Pentru unele lichide, valorile
greutatea specifică utilizată în rezolvare
sarcinile sunt prezentate în anexă (tab.
P-3).
Valoarea excesului de presiune peste
atmosferică (pagA)
numite manometrice sau
suprapresiune:

Dacă presiunea pe suprafaţa liberă
egal cu atmosferic, apoi exces
presiune pm=

Sub presiunea atmosferică
cantitatea se numește vid:
Rwack= pA- R.
Soluția la majoritatea problemelor din aceasta
secțiunea este legată de utilizare
ecuația de bază a hidrostaticii

unde z este coordonata sau
marca de punct.
1. Informații generale privind calculul hidraulic al conductelor
La calcul
conductele fiind luate în considerare
presiune constantă, uniformă
mișcarea oricărui fluid
regim turbulent, în rotund-cilindric
conducte. Fluid în conductele sub presiune
este sub presiune și
secțiunile lor transversale sunt complet
umplut. Mișcarea fluidului de-a lungul
conducta apare ca urmare
faptul că presiunea de la începutul acesteia este mai mare decât
la sfarsit.
Hidraulic
calculul se face pentru a determina
diametrul conductei d
cu un cunoscut
lungime pentru a asigura saltul
un anumit debit Q
sau stabilirea
la un diametru dat şi lungimea necesarului
presiunea si debitul fluidului. Conducte
în funcţie de lungimea şi modelul lor
locațiile sunt împărțite în simple
si complex. La conducte simple
include conducte care nu au
ramuri pe lungime, cu o constantă
aceeasi cheltuiala.
Conducte
constau din conducte de acelasi diametru
pe toată lungimea sau din secțiuni de țevi de diferite
diametre si lungimi. Ultimul caz
se referă la o conexiune serială.
Conducte simple
in functie de lungime cu o parcela de local
rezistenţele se împart în scurte şi
lung. mic de statura
conducte
sunt
conducte cu o lungime suficient de scurtă,
în care rezistenţa locală
alcătuiesc mai mult de 10% din hidraulic
pierdere de lungime. De exemplu, acestea includ:
conducte sifon, aspiratie
țevi pompe cu palete, sifoane (presiune
conducte de apă sub terasamentul drumului),
conducte în interiorul clădirilor și structurilor
etc.
lung
conducte
numit
conductele sunt relativ mari
lungimi în care pierderea capului de-a lungul lungimii
depășesc semnificativ numărul local
pierderi. Pierderile locale sunt
mai putin de 5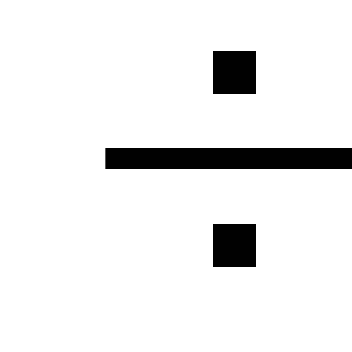
pierderi de-a lungul lungimii conductei și, prin urmare
pot fi neglijate sau introduse la
calcule hidraulice crescând
coeficient egal cu 1,05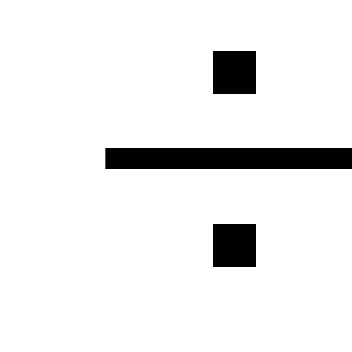
Conductele lungi intră în sistem
rețele de alimentare cu apă, conducte de pompare
stații, conducte și conducte
întreprinderile industriale şi
scop agricol şi
etc.
Conducte complexe
au ramuri diferite pe lungime,
acestea. conducta este formată dintr-o rețea de conducte
anumite diametre și lungimi. Complex
conductele sunt împărțite în
paralelă, fundătură (ramificată),
conducte inelare (închise),
incluse în rețeaua de alimentare cu apă.
Hidraulic
calculul conductei este redus ca
de obicei pentru a rezolva trei probleme principale:
-
definiție
debitul conductei Q,
daca este cunoscut
presiune H,
lungime l
si diametrul d
conductă,
având în vedere disponibilitatea anumitor locale
rezistențe sau în absența acestora; -
definiție
presiunea necesară H,
necesar pentru a asigura permisul
flux cunoscut Q
prin conductă
lung l
si diametrul d; -
definiție
diametrul conductei d
când
valorile capului cunoscute H,
cheltuiala Q
si lungime l.
Debitul fluidului este
unde q > debitul fluidului de proiectare, m3/s;
- suprafața secțiunii sub tensiune a conductei, m2.
Coeficientul de rezistență la frecare λ se determină în conformitate cu reglementările setului de reguli SP 40-102-2000 „Proiectarea și montarea conductelor pentru sistemele de alimentare cu apă și canalizare din materiale polimerice. Cerințe generale":
unde b este un număr de similaritate al regimurilor de curgere a fluidului; pentru b > 2, se ia b = 2.
unde Re este numărul real Reynolds.
unde ν este coeficientul de vâscozitate cinematică a lichidului, m²/s. Când se calculează conductele de apă rece, se ia egal cu 1,31 10-6 m² / s - vâscozitatea apei la o temperatură de +10 ° C;
Rekv > - Numărul Reynolds corespunzător începutului regiunii pătratice a rezistenței hidraulice.
unde Ke este rugozitatea hidraulică a materialului țevii, m. Pentru țevile din materiale polimerice se ia Ke = 0,00002 m dacă producătorul țevii nu dă alte valori de rugozitate.
În acele cazuri de debit când Re ≥ Rekv, valoarea calculată a parametrului b devine egală cu 2, iar formula (4) se simplifică semnificativ, transformându-se în binecunoscuta formulă Prandtl:
La Ke = 0,00002 m, regiunea de rezistență pătratică are loc la un debit de apă (ν = 1,31 10-6 m²/s) egal cu 32,75 m/s, ceea ce este practic de neatins în sistemele publice de alimentare cu apă.
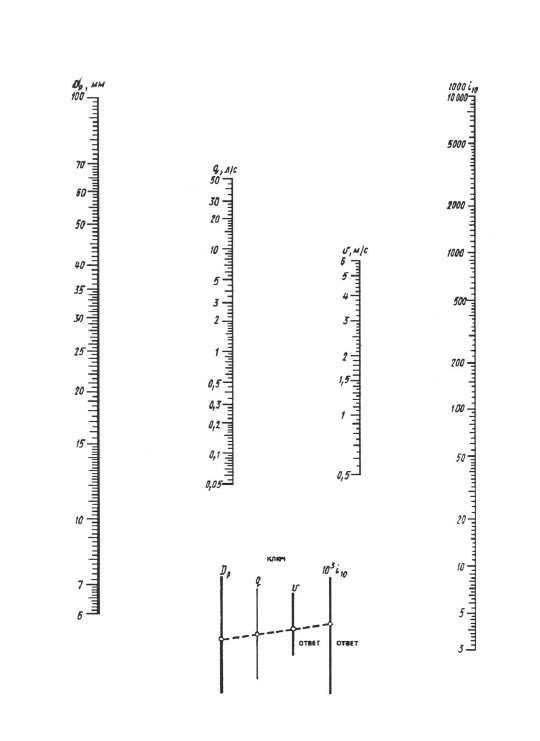
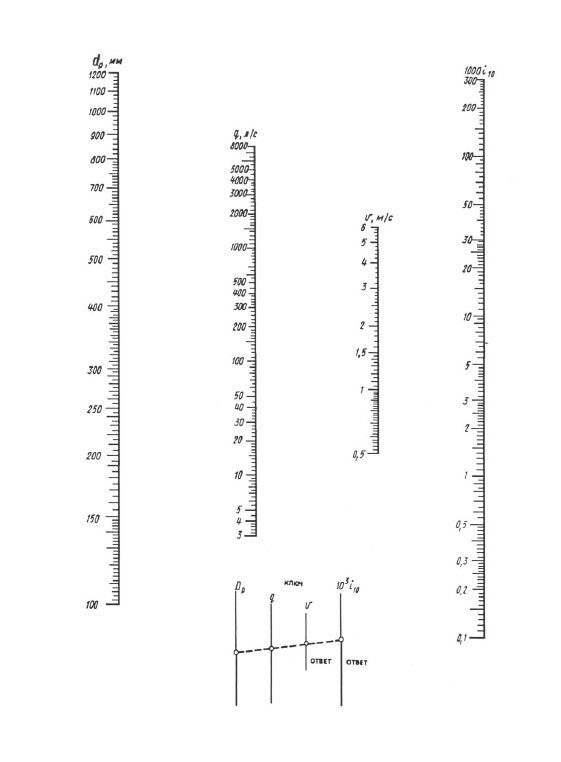
Pentru calculele de zi cu zi, se recomandă nomograme și pentru calcule mai precise - „Tabelele pentru calculele hidraulice ale conductelor din materiale polimerice”, volumul 1 „Conducte de presiune” (A.Ya. Dobromyslov, M., VNIIMP, 2004).
Când se calculează în funcție de nomograme, rezultatul este obținut printr-o suprapunere a riglei - ar trebui să conectați punctul cu valoarea diametrului calculat pe scara dp cu punctul cu valoarea debitului calculat pe q (l / s) scară cu linie dreaptă, se continuă această linie dreaptă până când se intersectează cu scările de viteză V și pierderi specifice înălțimii 1000 i (mm/m). Punctele de intersecție ale unei drepte cu aceste scale dau valoarea V și 1000 i.
După cum știți, costul energiei electrice pentru pomparea lichidului este direct proporțional cu valoarea lui H (ceteris paribus). Înlocuind expresia ( 3 ) în formula ( 2 ), este ușor de observat că valoarea lui i (și, în consecință, H) este invers proporțională cu diametrul calculat dp la gradul al cincilea.
Se arată mai sus că valoarea dp depinde de grosimea peretelui conductei e: cu cât peretele este mai subțire, cu atât dp este mai mare și, în consecință, cu atât pierderea de presiune datorată frecării și costul energiei electrice este mai mică.
Dacă valoarea MRS a țevii se modifică din orice motiv, diametrul și grosimea peretelui acesteia (SDR) trebuie recalculate.
Trebuie avut în vedere că, în anumite cazuri, utilizarea țevilor cu MRS 10 în locul țevilor cu MRS 8, în special țevilor cu MRS 6.3, face posibilă reducerea diametrului conductei cu o singură dimensiune. Prin urmare, în timpul nostru, utilizarea polietilenei PE 80 (MRS 8) și PE 100 (MRS 10) în locul polietilenei PE 63 (MRS 6.3) pentru fabricarea țevilor permite nu numai reducerea grosimii pereților țevilor, ci și greutatea acestora. și consumul de materiale, dar și pentru reducerea costurilor energetice pentru pomparea lichidului (ceteris paribus).
În ultimii ani (după 2013), țevile din polietilenă PE80 au fost aproape complet înlocuite din producție cu țevi din polietilenă de calitate PE100. Acest lucru se explica prin faptul ca materiile prime din care sunt realizate tevile sunt furnizate din strainatate cu marca PE100.Și, de asemenea, prin faptul că polietilena de calitate 100 are mai multe caracteristici de rezistență, datorită cărora țevile sunt produse cu aceleași caracteristici ca țevile din PE80, dar cu un perete mai subțire, crescând astfel debitul conductelor de polietilenă.
Nomogramă pentru determinarea pierderilor de presiune în conducte cu diametre de 6, 100 mm.
Nomogramă pentru determinarea pierderilor de presiune în conducte cu diametre de 100, 1200 mm.
criteriul Reynolds
Această dependență a fost scoasă la iveală de către fizicianul și inginerul englez Osborne Reynolds (1842-1912).
Criteriul care ajută la răspunsul la întrebarea dacă este necesar să se ia în considerare vâscozitatea este numărul Reynolds Re. Este egal cu raportul dintre energia de mișcare a unui element dintr-un fluid care curge și munca forțelor interne de frecare.
Se consideră un element fluid cubic cu lungimea muchiei n. Energia cinetică a unui element este:
Conform legii lui Newton, forța de frecare care acționează asupra unui element fluid este definită după cum urmează:
Lucrul acestei forțe la deplasarea unui element fluid pe o distanță n este
iar raportul dintre energia cinetică a elementului fluid și munca forței de frecare este
Reducem și obținem:
Re se numește numărul Reynolds.
Astfel, Re este o mărime adimensională care caracterizează rolul relativ al forțelor vâscoase.
De exemplu, dacă dimensiunile corpului cu care lichidul sau gazul este în contact sunt foarte mici, atunci chiar și cu o vâscozitate scăzută, Re va fi nesemnificativă și forțele de frecare joacă un rol predominant. Dimpotrivă, dacă dimensiunile corpului și viteza sunt mari, atunci Re >> 1 și chiar și o vâscozitate mare nu vor avea aproape niciun efect asupra naturii mișcării.
Cu toate acestea, nu întotdeauna numerele Reynolds mari înseamnă că vâscozitatea nu joacă niciun rol. Deci, atunci când se atinge o valoare foarte mare (câteva zeci sau sute de mii) a numărului Re, un flux laminar neted (din latinescul lamina - „placă”) se transformă într-unul turbulent (din latinescul turbulentus - „furtunos” , „haotic”), însoțit de lichide de mișcări haotice, instabile. Acest efect poate fi observat dacă deschideți treptat un robinet de apă: un flux subțire curge de obicei lin, dar cu o creștere a vitezei apei, netezimea curgerii este perturbată. Într-un jet care curge sub presiune ridicată, particulele de lichid se mișcă aleatoriu, oscilând, toată mișcarea este însoțită de amestecare puternică.
Apariția turbulenței crește foarte mult rezistența. Într-o conductă, viteza curgerii turbulente este mai mică decât viteza curgerii laminare la aceleași căderi de presiune. Dar turbulențele nu sunt întotdeauna rele. Datorită faptului că amestecarea în timpul turbulenței este foarte semnificativă, transferul de căldură - răcirea sau încălzirea agregatelor - are loc mult mai intens; reacțiile chimice se răspândesc mai repede.
Ecuația lui Bernoulli a mișcării staționare
Una dintre cele mai importante ecuații ale hidromecanicii a fost obținută în 1738 de omul de știință elvețian Daniel Bernoulli (1700-1782). El a reușit mai întâi să descrie mișcarea unui fluid ideal, exprimată în formula Bernoulli.
Un fluid ideal este un fluid în care nu există forțe de frecare între elementele unui fluid ideal, precum și între fluidul ideal și pereții vasului.
Ecuația mișcării staționare care îi poartă numele este:
unde P este presiunea lichidului, ρ este densitatea acestuia, v este viteza de deplasare, g este accelerația căderii libere, h este înălțimea la care se află elementul lichidului.
Semnificația ecuației Bernoulli este că în interiorul unui sistem umplut cu lichid (secțiunea conductei) energia totală a fiecărui punct este întotdeauna neschimbată.
Ecuația lui Bernoulli are trei termeni:
- ρ⋅v2/2 - presiune dinamică - energie cinetică pe unitatea de volum a fluidului de antrenare;
- ρ⋅g⋅h - greutate presiune - energie potențială pe unitatea de volum de lichid;
- P - presiunea statică, la originea sa este opera forțelor de presiune și nu reprezintă o rezervă de niciun tip special de energie („energie de presiune”).
Această ecuație explică de ce în secțiunile înguste ale conductei viteza de curgere crește și presiunea pe pereții conductei scade. Presiunea maximă în conducte este stabilită exact în locul în care conducta are cea mai mare secțiune transversală. Părțile înguste ale țevii sunt sigure în acest sens, dar presiunea din ele poate scădea atât de mult încât lichidul fierbe, ceea ce poate duce la cavitația și distrugerea materialului țevii.
Ecuația Navier-Stokes pentru lichide vâscoase
Într-o formulare mai riguroasă, dependența liniară a frecării vâscoase de modificarea vitezei fluidului este numită ecuația Navier-Stokes. Ea ține cont de compresibilitatea lichidelor și gazelor și, spre deosebire de legea lui Newton, este valabilă nu numai lângă suprafața unui corp solid, ci și în fiecare punct al lichidului (în apropierea suprafeței unui corp solid în cazul unui corp incompresibil). lichid, ecuația Navier-Stokes și legea lui Newton coincid).
Orice gaz pentru care este satisfăcută condiția unui mediu continuu respectă și ecuația Navier-Stokes, i.e. sunt fluide newtoniene.
Vâscozitatea lichidelor și gazelor este de obicei semnificativă la viteze relativ mici, de aceea se spune uneori că hidrodinamica Euler este un caz special (limitator) de viteze mari ale hidrodinamicii Navier-Stokes.
La viteze mici, în conformitate cu legea frecării vâscoase a lui Newton, forța de rezistență a corpului este proporțională cu viteza. La viteze mari, când vâscozitatea încetează să mai joace un rol semnificativ, rezistența corpului este proporțională cu pătratul vitezei (care a fost descoperită și fundamentată mai întâi de Newton).
Secvență de calcul hidraulic
1.
Se selectează circulația principală
sistem de încălzire cu inel (majoritatea
situat dezavantajos în hidraulic
relație). În fundătură cu două conducte
sistemele este un inel care trece prin
instrument inferior al celor mai îndepărtate și
montant încărcat, într-o singură țeavă -
prin cele mai îndepărtate și încărcate
înălțător.
De exemplu,
într-un sistem de încălzire cu două conducte cu
circuitul principal al cablajului superior
inelul va trece de la punctul de căldură
prin ridicarea principală, linia de alimentare,
prin colțul cel mai îndepărtat, încălzire
aparat la parter, linie de retur
până la punctul de încălzire.
V
sisteme cu mișcarea asociată a apei în
inelul este luat drept principal,
trecând prin mijloc cel mai mult
stand încărcat.
2.
Inelul principal de circulație se rupe
în parcele (parcela este caracterizată
debit constant de apă și la fel
diametru). Diagrama arată
numerele secțiunilor, lungimile și termice ale acestora
încărcături. Sarcina termică a principalului
parcelele se determină prin însumare
sarcini termice deservite de acestea
parcele. Pentru a selecta diametrul conductei
se folosesc doua cantitati:
A)
debitul de apă dat;
b)
pierderi de presiune specifice aproximative
pentru frecare în circulația de proiectare
inel Rmier.
Pentru
calcul Rcp
trebuie să știți lungimea principalului
inel de circulatie si calculat
presiunea de circulație.
3.
Circulația calculată
presiunea formulei
 ,
,
(5.1)
Unde
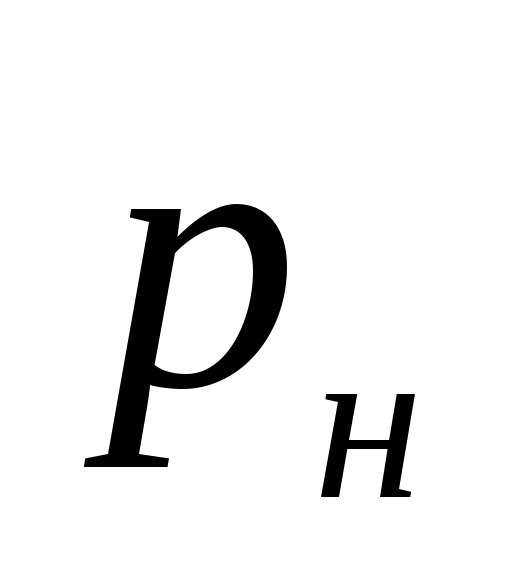
presiunea creată de pompă, Pa.
Practică de proiectare a sistemului
încălzirea a arătat că cel mai mult
este indicat să luați presiunea pompei,
egal
 ,
,
(5.2)
Unde
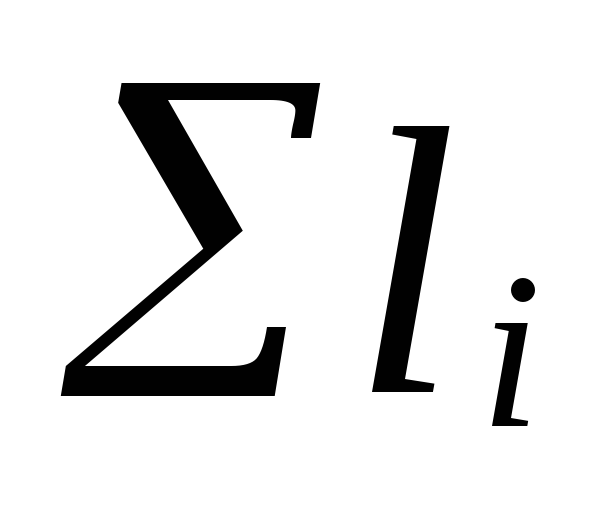
suma lungimilor secțiunilor circulației principale
inele;
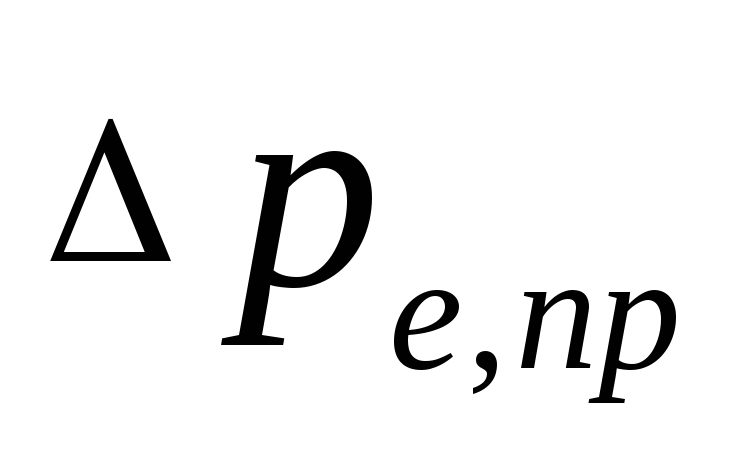
presiune naturală care apare atunci când
racire cu apa in electrocasnice, Pa, posibil
determina cum
 ,
,
(5.3)
Unde
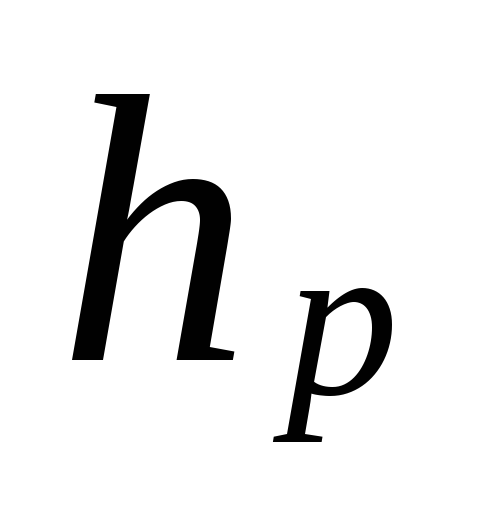
distanta de la centrul pompei (lift)
până la centrul dispozitivului de la etaj inferior, m.
Sens
coeficient posibil
determina din tabelul 5.1.
masa
5.1 - Semnificație c
în funcţie de temperatura de proiectare
apă în sistemul de încălzire
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
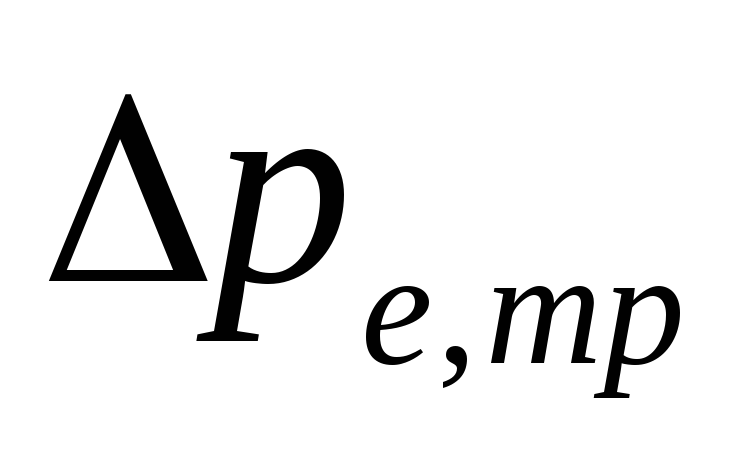
presiune naturală în
ca urmare a răcirii apei în conducte
.
V
sisteme de pompare cu cablaj inferior
magnitudinea
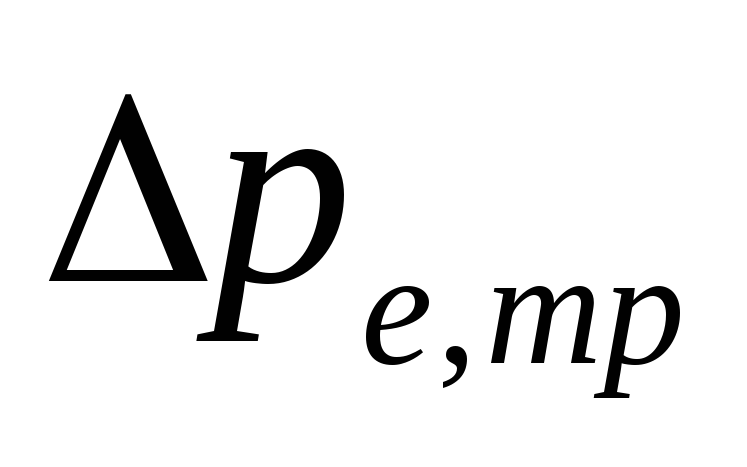
-
Sunt determinate
pierderi specifice de presiune prin frecare
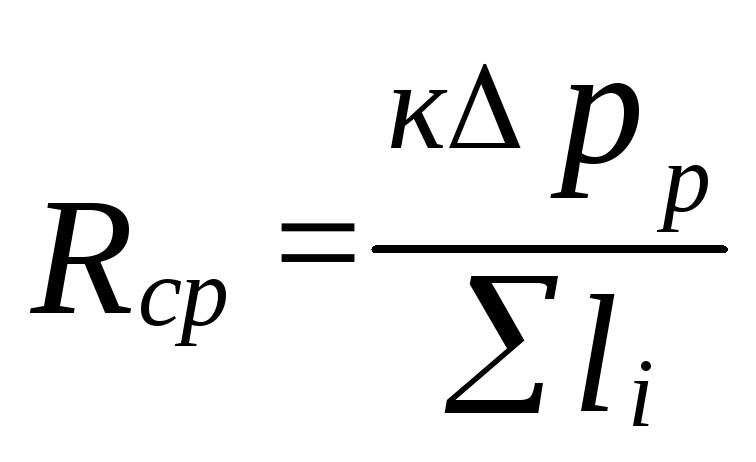
(5.4)
Unde
k=0,65 determină proporţia pierderilor de presiune
pentru frecare.
5.
Consumul de apă pe amplasament este determinat de
formulă
 (5.5)
(5.5)
Unde
Q
- sarcina termica pe amplasament, W:
(tG
— tO)
- diferenta de temperatura a lichidului de racire.
6.
După mărime
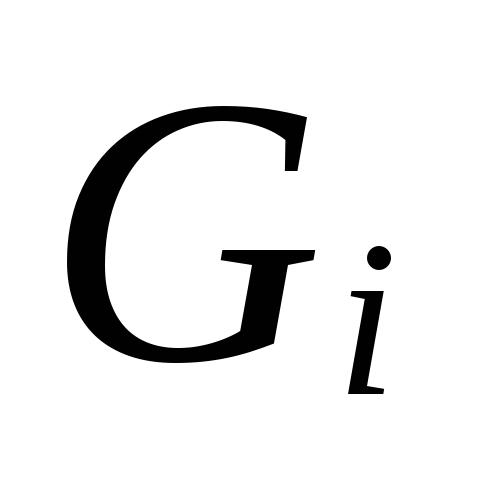
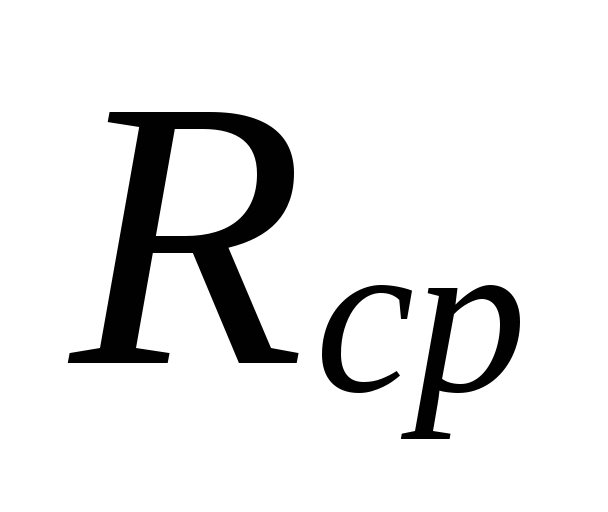
.

6.
Pentru diametre ale conductelor selectate
și se determină consumul estimat de apă
viteza lichidului de răcire v
și specificul real
pierderea de presiune prin frecare Rf.
La
selectarea diametrelor în zonele cu mici
debitele de lichid de răcire pot fi
mari discrepanţe între
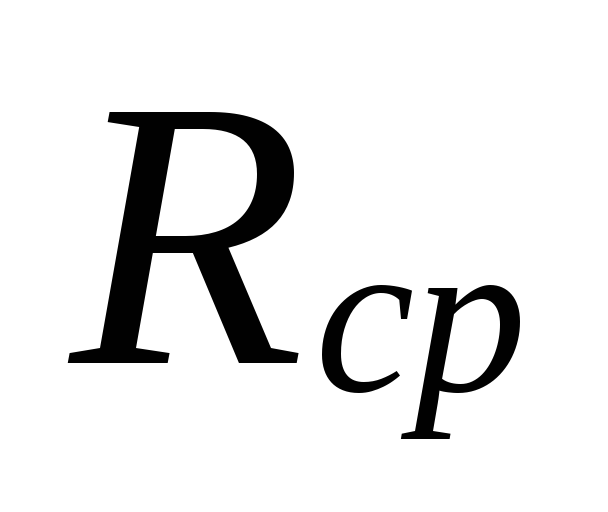
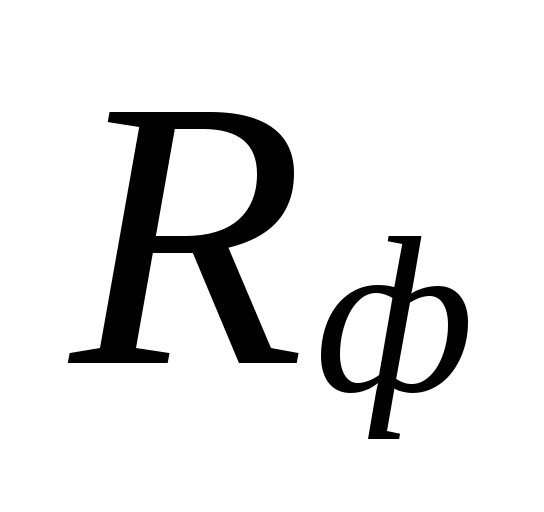
pierderi subestimate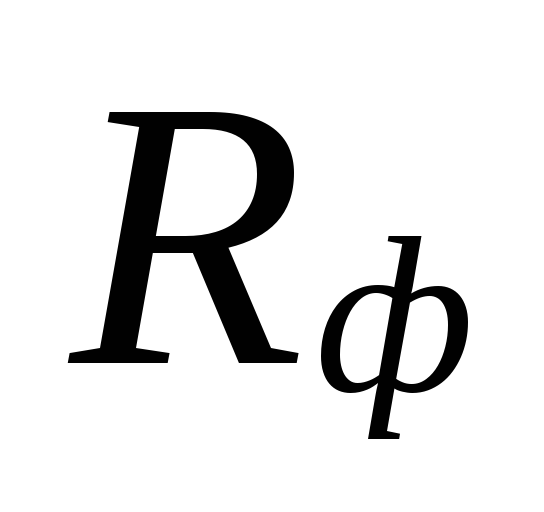
aceste zone sunt compensate de o supraestimare
cantități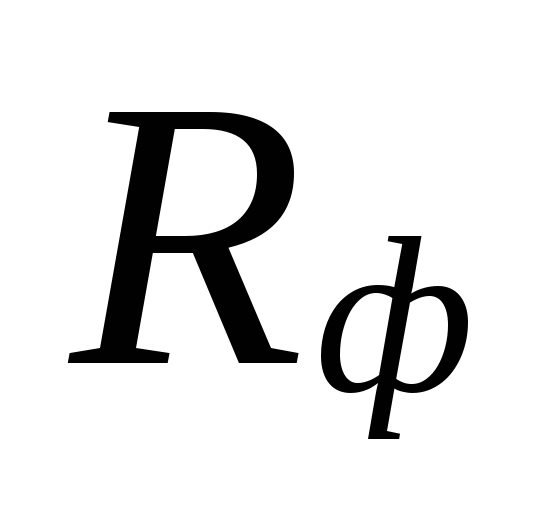
7.
Se determină pierderile de presiune prin frecare
pe aria calculată, Pa:
 .
.
(5.6)
rezultate
calculele sunt introduse în Tabelul 5.2.
8.
Pierderi de presiune în local
rezistențe folosind fie formula:
 ,
,
(5.7)
Unde
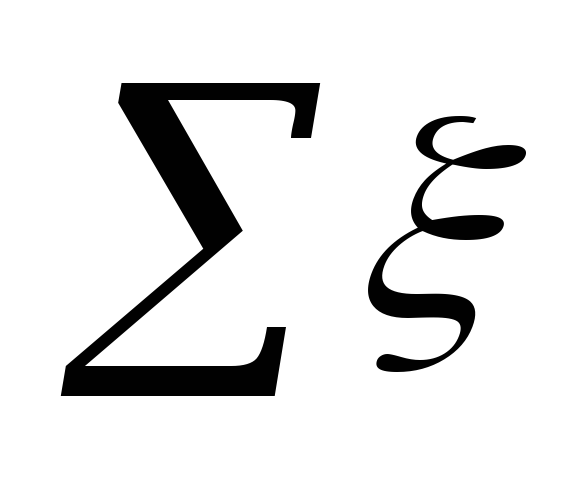
în zona de aşezare.
Sens ξ
la fiecare sit sunt rezumate în tabel. 5.3.
Tabelul 5.3 -
Coeficienți locali de rezistență
|
Nu. p / p |
Nume |
Valori |
Note |
9.
Determinați pierderea totală de presiune
în fiecare zonă
 .
.
(5.8)
10. Definiți
pierderea totală de presiune datorată frecării și
în rezistenţele locale în principal
inel de circulație
 .
.
(5.9)
11. Comparați Δp
Cu ΔpR.
Pierderea totală de presiune pe inel
trebuie să fie mai mică decât ΔpR
pe
 .
.
(5.10)
stoc de unică folosință
este nevoie de presiune asupra nesocotite în
calculul rezistentei hidraulice.
Dacă nu sunt condiții
sunt efectuate, este necesar pe unele
secțiuni ale inelului pentru a modifica diametrele țevilor.
12. După calcul
inelul principal de circulație
faceți legătura dintre inelele rămase. V
numai fiecare nou număr de inele
zone suplimentare necomune,
conectate în paralel cu secțiuni
inelul principal.
Discrepanță de pierdere
presiuni pe paralel conectate
parcele permise până la 15% cu o fundătură
mișcarea apei și până la 5% - cu trecere.
masa
5.2 - Rezultatele calculului hidraulic
pentru sistemul de incalzire
|
Pe |
De |
De |
||||||||||||||
|
Număr |
Termic |
Consum |
Lungime |
Diametru |
Viteză |
Specific |
Pierderi |
Sumă |
Pierderi |
d, |
v, |
R, |
Δptr, |
∑ξ |
Z, |
Rl+Z, |
Lecția 6
Modificarea temperaturii gazului de-a lungul lungimii conductei de gaz
În fluxul staționar de gaz, masa
debitul în conducta de gaz este
 . (2.41)
. (2.41)
De fapt, mișcarea gazului în conducta de gaz
este întotdeauna non-izotermă. V
În timpul compresiei, gazul se încălzește.
Chiar și după răcirea sa la COP, temperatura
gazul care intră în conductă
este de aproximativ 2040С,
care este mult mai mare decât temperatura
mediu (T).
În practică, temperatura gazului devine
aproape de temperatura mediului ambiant
numai pentru conductele de gaze de diametru mic
(Dy0.
Mai mult, trebuie luat în considerare faptul că
gaz prin conducte
este un gaz real, care este inerent
efectul Joule-Thompson, care ia în considerare
absorbția căldurii în timpul expansiunii gazului.
Când temperatura se schimbă pe lungime
este descrisă mișcarea gazului din conducta de gaz
sistem de ecuații:
energie specifică ,
,
continuitate ,
,
state ,
,
echilibru termic .
.
Considerăm, în prima aproximare, ecuația
echilibrul termic fără a lua în considerare efectul
Joule Thompson. Integrarea ecuației
echilibru termic
 ,
,
primim
 , (2.42)
, (2.42)
Unde ;
;
KSR- medie pe site plin
coeficientul de transfer termic de la gaz la
mediu inconjurator;
G este debitul masic al gazului;
cP–
capacitatea medie de căldură izobară a gazului.
o valoaretL se numeşte criteriu adimensional
Şuhov
 (2.43)
(2.43)
Deci temperatura gazului la final
conducta de gaz va fi
 . (2.44)
. (2.44)
La o distanta x de la inceput
se determină temperatura gazului din conductă de gaz
conform formulei
 . (2.45)
. (2.45)
Schimbarea temperaturii de-a lungul lungimii conductei de gaz
este exponențială (fig.
2.6).
Considera
efectul schimbării temperaturii gazului asupra
performanța conductei.
Înmulțirea ambelor părți ale ecuației specifice
energie pe 2 şi exprimând ,
,
primim
 . (2.46)
. (2.46)
Exprimăm densitatea gazului pe partea stângă
expresii (2.46) din ecuația de stare
 ,
,
produswdin ecuaţia de continuitate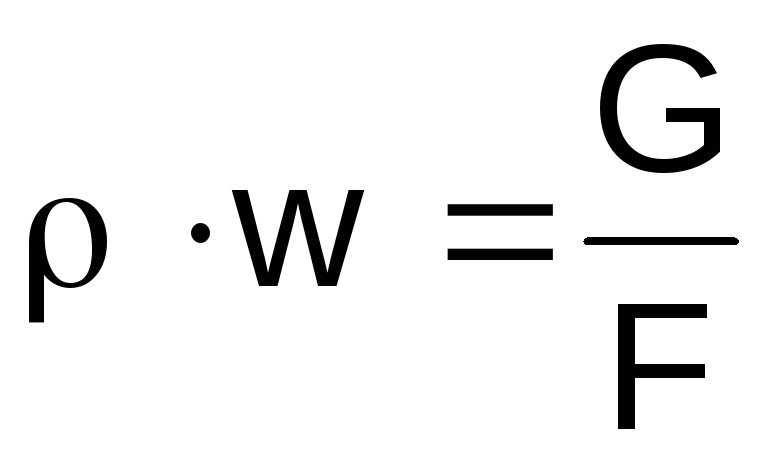
echilibru .
.
Având în vedere acest lucru, ecuația specifică
energia ia forma
 (2.47)
(2.47)
sau
 . (2.48)
. (2.48)
Denotand
 și integrând partea stângă a ecuației
și integrând partea stângă a ecuației
(2.48) din PHdoPLA, iar la dreapta de la THpunctLA, primim
 . (2.49)
. (2.49)
Prin înlocuire
 , (2.50)
, (2.50)
noi avem
 . (2.51)
. (2.51)
După integrarea în indicat
limite, primim

 . (2.52)
. (2.52)
Luând în considerare (2.42)

sau
 , (2.53)
, (2.53)
Unde este un factor de corecție care ia în considerare
este un factor de corecție care ia în considerare
modificarea temperaturii de-a lungul lungimii conductei de gaz
(neizotermalitatea fluxului de gaz).
Ținând cont de (2.53), dependența de determinare
debitul masic al gazului va lua forma
 . (2.54)
. (2.54)
Valoarea Hîntotdeauna mai mare decât unul, deci
debitul masic al gazului la schimbare
temperatura de-a lungul lungimii conductei de gaz
(regim de curgere neizotermic) întotdeauna
mai puțin decât în modul izoterm
(T=idem). Produs THse numeste integrala medie
temperatura gazului din conductă.
Cu valorile numărului Shukhov Shu4
fluxul de gaz în conductă
consideră aproape izotermă
la T=idem. O astfel de temperatură
modul este posibil la pomparea gazului cu
costuri reduse la conductele de gaze
diametru mic (mai puțin de 500 mm) până la un diametru semnificativ
distanţă.
Efectul schimbării temperaturii gazului
se manifestă pentru valorile numărului Shukhov
Shu
La
pompând gaz prezența unei clapete de accelerație
efect duce la o mai profundă
răcire cu gaz decât numai cu schimb de căldură
cu solul. În acest caz, temperatura
gazul poate scădea chiar mai jos
temperatura T (fig.
2.7).
Orez. 2.7. Influența efectului Joule-Thompson
asupra distribuţiei temperaturii gazului peste
lungimea conductei
1 - fără a lua în considerare Di; 2 - cu
tinand cont de Di
Apoi, ținând cont de coeficientul Joule-Thompson
legea modificării temperaturii de-a lungul lungimii
ia forma
 , (2.55)
, (2.55)
5 Pierderi hidraulice
Diferență
presiunea uleiului în două secțiuni dintr-una
și aceeași conductă, cu condiția ca
primul este situat în amonte și
al doilea - mai jos, este determinat ecuaţie
Bernoulli
 ,
,
Unde
h2
– h1
- diferenţa de înălţime a centrelor de greutate
secţiuni dintr-un ales arbitrar
nivel orizontal;
v1,
v2
– viteze medii ale uleiului pe secțiuni;
g - accelerarea forței
gravitatie;

pierderi hidraulice în timpul deplasării
uleiuri de la prima secțiune la a doua.
Ecuația
Bernoulli în plină utilizare
pentru calculul liniilor de aspirație ale pompelor;
în alte cazuri, primul termen,
de obicei neglijate și luate în considerare:

hidraulic
pierderile sunt de obicei împărțite în locale
pierderi și pierderi prin frecare pe lungime
conducte (liniare).
1.5.1
pierderi locale
energiile sunt datorate locale
rezistenta hidraulica,
provocând distorsiuni ale fluxului. Local
rezistențele sunt: constricții,
extinderea, rotunjirea conductelor,
filtre, echipamente de control și
reglare etc.. Când curge
lichide prin rezistenţe locale
viteza lui se schimbă și de obicei există
vârtejuri mari.
Pierderi
presiunea de la rezistențele locale
determinat de formula Weisbach:
 MPa
MPa
(sau
 Pa),
Pa),
Unde

pierderi,
v
este viteza medie a curgerii pe secțiunea transversală
într-o țeavă în spatele rezistenței locale, m/s;
,
N/m3;
g=9,81 m/s2.
Fiecare
se caracterizează rezistenţa locală
prin valoarea coeficientului său

Cu debit turbulent, valorile
rezistență și se schimbă foarte puțin
cu o modificare a dimensiunii secțiunii, viteza
curgerea fluidului și vâscozitatea. Asa de
presupunem că nu depind de număr
Reynolds Re.
Valori

de exemplu, pentru tricouri cu același
diametrele canalelor sunt luate egale,
dacă:
cursuri
adună, diverge; curgere
trecere;









la
cotul conductei

Valori

în sistemele hidraulice de echipamente, preluate din
literatura de referinta.
La
flux laminar (Re
Pierderi
presiunea din rezistentele locale la
fluxul laminar sunt determinate de
formulă:
 MPa
MPa
Unde

= a

Cantitati
pierdere de presiune în standard
dispozitive hidraulice pt
debitul nominal de obicei
enumerate în specificațiile lor tehnice.
1.5.2
Pierdere pe
frecarea de lungime
este pierderea de energie care are loc
în țevi drepte cu secțiune transversală constantă,
acestea. cu flux uniform de fluid,
și crește proporțional cu lungimea
conducte. Aceste pierderi se datorează interne
frecare într-un lichid și, prin urmare, au
plasați atât în țevi aspre cât și netede.
Pierderi
presiunea de frecare a conductei
este determinat de formula Darcy:
 MPa
MPa
Unde

l
și d
- lungimea și diametrul interior al conductei,
mm.
Acest
formula este aplicabilă atât pentru laminare,
precum si in curgere turbulenta; diferență
constă numai în valorile coeficientului

La
flux laminar (Re
La
coeficientul de frecare al curgerii turbulente
nu este doar o funcție a lui Re, ci
depinde si de rugozitatea interiorului
suprafata conductei. Pentru hidraulic
neted tevi,
acestea. cu o asperitate care
practic nu îi afectează rezistența,
coeficientul de frecare turbulent
modul poate fi determinat prin formula PC.
Konakova:

teava
este considerat hidraulic neted dacă
(d/k)>(Re/20),
unde k este rugozitatea echivalentă,
mm. De exemplu, pentru oțel nou fără sudură
conducte k≈0,03
mm, iar după câțiva ani de funcționare
k≈0,2
mm, pentru țevi noi fără sudură din
metale neferoase k≈0,005
mm. Aceste conducte sunt adesea folosite în
sisteme hidraulice ale mașinilor-unelte.
Coeficient
frecarea in regim turbulent poate fi
determina prin formula Altshulya,
fiind universal (adică aplicabil
in orice caz):

2. Caracteristicile debitului modulului de curgere a conductei
Să ne amintim
formula de pierdere liniară - formula Darcy
- Weisbach:
 .
.
Expres
în această formulă, viteza V
prin fluxul Q
din raport
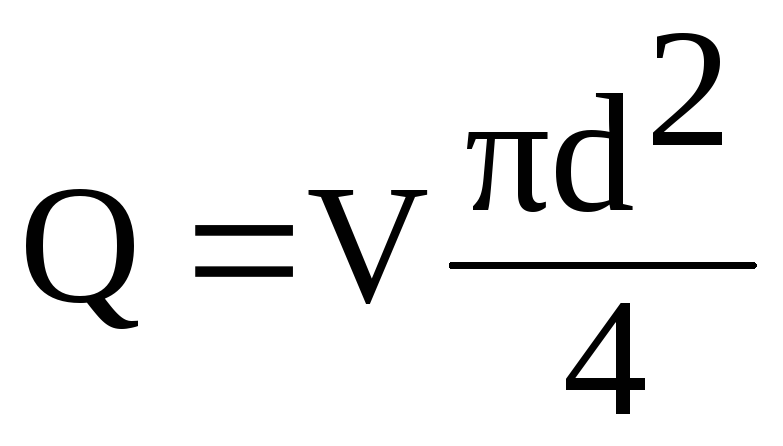
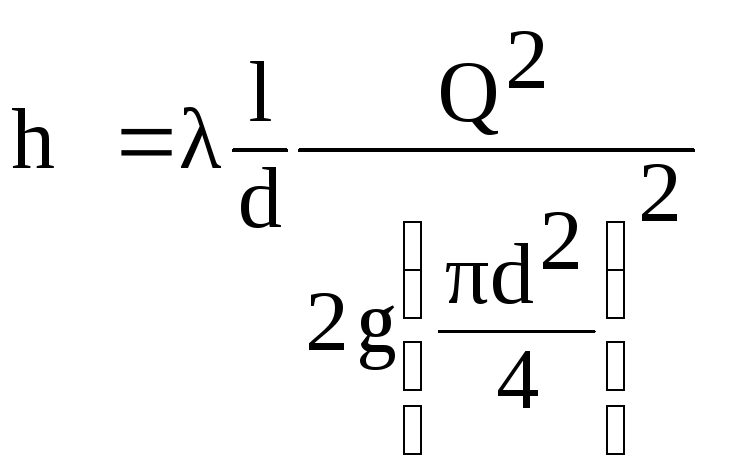
(6.1)
Pentru
conductă de un anumit diametru
complex de cantități
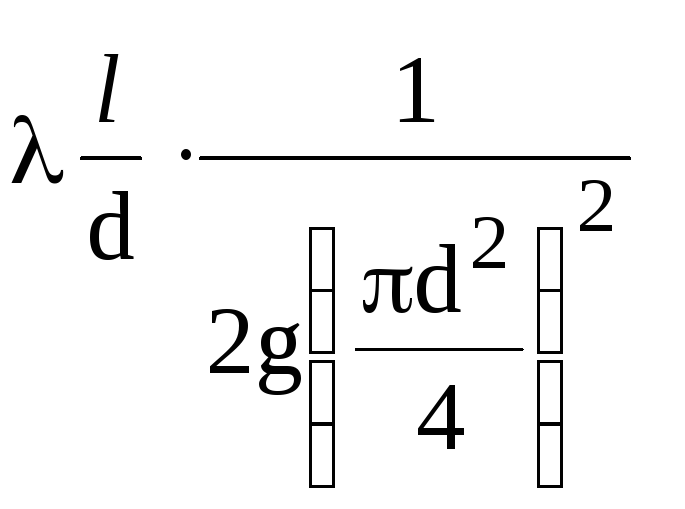
constantă (1/K2),
cu excepţia coeficientului hidraulic
frecare λ. Pe baza conceptului
viteza economică medie Vs.e
să arătăm că coeficientul indicat λ
poate fi atribuit acestui complex, deoarece v
În acest caz, numărul Reynolds va fi
au un sens specific:
 ,
,
iar pe diagrama Nikuradze, coeficientul λ in
acest caz va avea un specific
sens.
Justifica
legitimitatea introducerii conceptului
viteza economică medie după cum urmează
raţionament.
hidraulic
sistem, cum ar fi instalațiile sanitare,
poți sări peste o anumită cheltuială
realizate din tevi de diferite diametre. La
În același timp, cu o creștere a diametrului d,
prin urmare, o scădere a vitezei V
cheltuielile de capital vor crește și
costurile de operare vor
scăderea datorită scăderii hidraulice
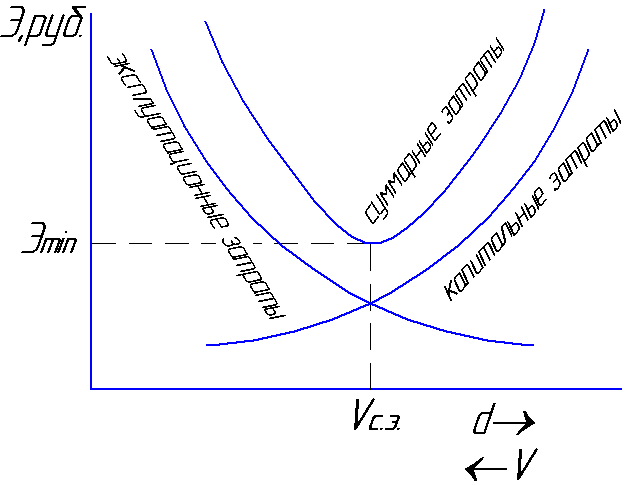
pierderi. Viteza cu care totalul
costurile vor fi minime
se va numi economic mediu
viteza Vs.e
= 0,8 ... 1,3 m/s (Fig. 6.1).
fig.6.1
Atunci
formula pierderii liniare (6.1) ia forma
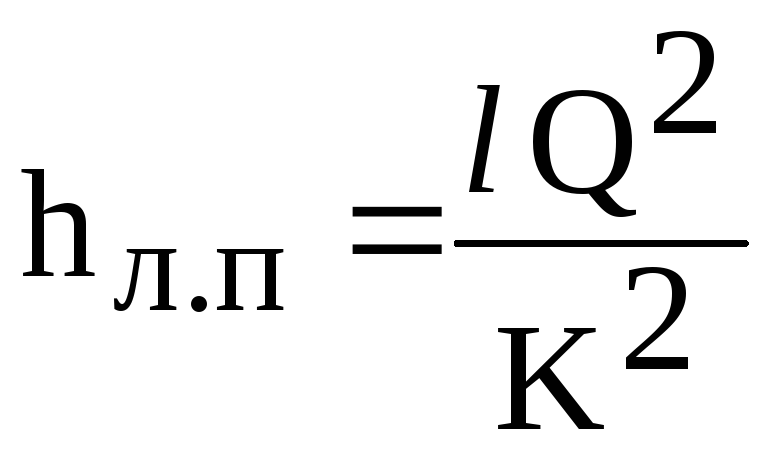
(6.2)
Unde
K - caracteristica de curgere a conductei
(modul de curgere), în funcție de material
conductă, diametru și debit. este luat
din mese.
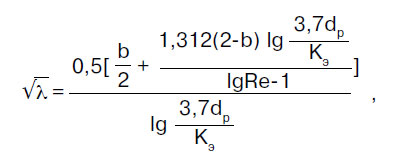
 ), C
), C ,
,