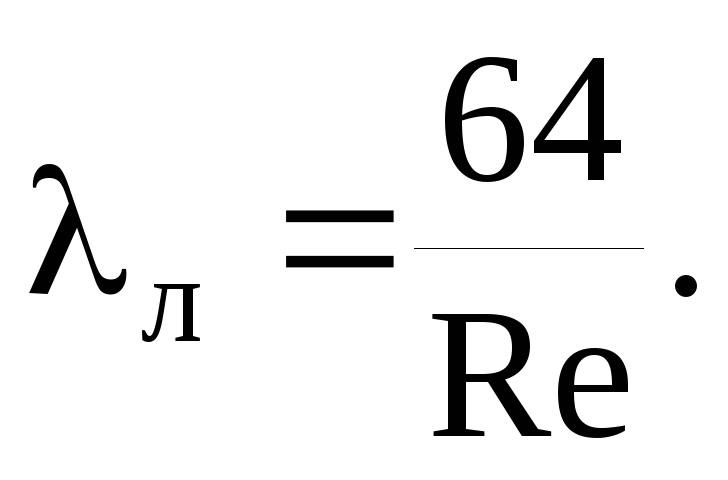1. Hydrostatický tlak
Hydrostatický tlak je
vnútorná tlaková sila v dôsledku
pôsobením vonkajších síl pôsobiacich na
daný bod v tekutine. Taký tlak
vo všetkých smeroch je rovnaký a závisí
o polohe bodu v kvapaline v pokoji.
Rozmer hydrostatického tlaku
v systéme MKGSS - kg / cm2 alebo t / m2,
v sústave SI - N/m2.
Základné jednotkové pomery
tlak:
|
kg/cm2 |
N/m2 |
|
|
technická atmosféra |
1 |
98066,5 |
|
milimeter vodného stĺpca |
0,0001 |
9,80665 |
|
milimeter ortuti |
0,00136 |
133,32 |
V praktických výpočtoch 1 technický
atmosféra \u003d 1 kg / cm2 \u003d 10 m vody. čl. =
735 mmHg čl. = 98070 N/m2.
Pre nestlačiteľnú tekutinu, ktorá je
v rovnováhe pod silou
gravitačná, plne hydrostatická
bodový tlak:
p=p+

kde p je tlak na voľnom
povrch kvapaliny;

výška h s plochou
prierez rovný jednej;
h - hĺbka ponoru
body;

Pre niektoré kvapaliny hodnoty
špecifická hmotnosť používaná pri riešení
úlohy sú uvedené v prílohe (tab.
P-3).
Hodnota nadmerného tlaku nad
atmosférický (sa)
nazývané manometrické, príp
pretlak:

Ak tlak na voľnú plochu
rovná atmosférickému, potom nadbytočnému
tlak pm=

Nedostatočný atmosférický tlak
množstvo sa nazýva vákuum:
Ršialený= pa- R.
Riešenie väčšiny týchto problémov
časť súvisí s používaním
základná rovnica hydrostatiky

kde z je súradnica alebo
bodová značka.
1. Všeobecné informácie o hydraulickom výpočte potrubí
Pri výpočte
potrubí
stály, rovnomerný tlak
pohyb akejkoľvek tekutiny
turbulentný režim, v okrúhlom valcovom
potrubia. Kvapalina v tlakovom potrubí
je pod tlakom a
ich prierezy sú úplne
naplnené. Pohyb tekutiny pozdĺž
v dôsledku toho vzniká potrubie
skutočnosť, že tlak na jej začiatku je väčší ako
na koniec.
Hydraulické
výpočet sa robí s cieľom určiť
priemer potrubia d
so známym
dĺžka, aby sa zabezpečilo preskočenie
určitý prietok Q
alebo založenie
pri danom priemere a dĺžke požadovaného
tlak a prietok tekutiny. Potrubia
v závislosti od ich dĺžky a vzoru
miesta sú rozdelené na jednoduché
a komplexné. K jednoduchým potrubiam
zahŕňa potrubia, ktoré nemajú
vetvy po dĺžke, s konštant
rovnaký výdavok.
Potrubia
pozostávajú z rúrok rovnakého priemeru
po celej dĺžke alebo z rôznych častí rúr
priemery a dĺžky. Posledný prípad
označuje sériové pripojenie.
Jednoduché potrubia
v závislosti od dĺžky s pozemkom miestnych
odpory sa delia na krátke a
dlhý. krátky
potrubia
sú
potrubia s dostatočne krátkou dĺžkou,
v ktorom lokálny odpor
tvoria viac ako 10 % hydrauliky
strata dĺžky. Zahŕňajú napríklad:
sifónové potrubia, sacie
potrubia lamelových čerpadiel, sifóny (tlak
vodovodné potrubie pod cestným násypom),
potrubia vo vnútri budov a konštrukcií
atď.
dlhý
potrubia
volal
potrubia sú pomerne veľké
dĺžky, pri ktorých dochádza k strate hlavy po dĺžke
výrazne prevyšujú miestne
straty. Lokálne straty sú
menej ako 5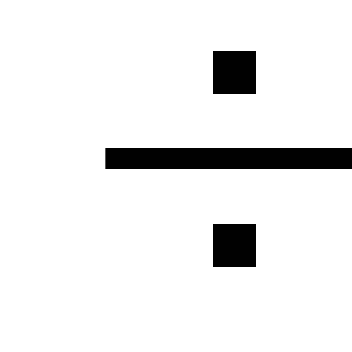
straty po dĺžke potrubia, a preto
môžu byť zanedbané alebo zavedené pri
hydraulické výpočty sa zvyšujú
koeficient rovný 1,05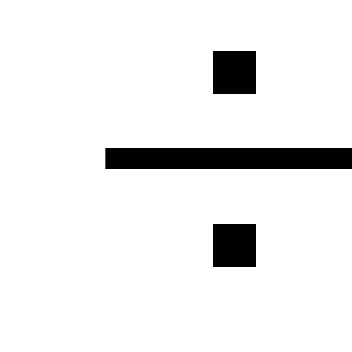
Do systému vstupujú dlhé potrubia
vodovodné siete, čerpacie potrubia
stanice, potrubia a potrubia
priemyselné podniky a
poľnohospodársky účel a
atď.
Komplexné potrubia
mať rôzne vetvy pozdĺž dĺžky,
tie. potrubie pozostáva zo siete potrubí
určité priemery a dĺžky. Komplexné
potrubia sa delia na
paralelný, slepý koniec (rozvetvený),
prstencové (uzavreté) potrubia,
zahrnuté do vodovodnej siete.
Hydraulické
výpočet potrubia je znížený ako
zvyčajne na vyriešenie troch hlavných problémov:
-
definícia
prietok potrubia Q,
ak je známy
tlak H,
dĺžka l
a priemer d
potrubie,
vzhľadom na dostupnosť určitých miestnych
odpory alebo v ich neprítomnosti; -
definícia
požadovaný tlak H,
potrebné na zabezpečenie priepustky
známy tok Q
potrubím
dlhý l
a priemer d; -
definícia
priemer potrubia d
kedy
známe hodnoty hlavy H,
výdavok Q
a dĺžka l.
Rýchlosť prietoku tekutiny je
kde q > návrhový prietok kvapaliny, m3/s;
- plocha živej časti potrubia, m2.
Súčiniteľ odporu trenia λ sa určuje v súlade s predpismi súboru pravidiel SP 40-102-2000 „Projektovanie a montáž potrubí pre vodovody a kanalizácie z polymérnych materiálov. Všeobecné požiadavky":
kde b je určitý počet podobností režimov prúdenia tekutín; pre b > 2 sa berie b = 2.
kde Re je skutočné Reynoldsovo číslo.
kde ν je koeficient kinematickej viskozity kvapaliny, m²/s. Pri výpočte potrubí studenej vody sa berie ako 1,31 10-6 m² / s - viskozita vody pri teplote +10 ° C;
Rekv > - Reynoldsovo číslo zodpovedajúce začiatku kvadratickej oblasti hydraulického odporu.
kde Ke je hydraulická drsnosť materiálu potrubia, m. Pre potrubia vyrobené z polymérnych materiálov sa berie Ke = 0,00002 m, ak výrobca potrubia neudáva iné hodnoty drsnosti.
V tých prípadoch prietoku, keď Re ≥ Rekv, sa vypočítaná hodnota parametra b rovná 2 a vzorec (4) sa výrazne zjednoduší a zmení sa na známy Prandtlov vzorec:
Pri Ke = 0,00002 m sa oblasť kvadratického odporu vyskytuje pri prietoku vody (ν = 1,31 10-6 m²/s) rovnajúcej sa 32,75 m/s, čo je vo verejných vodovodoch prakticky nedosiahnuteľné.
Pre každodenné výpočty sa odporúčajú nomogramy a pre presnejšie výpočty - "Tabuľky pre hydraulické výpočty potrubí vyrobených z polymérnych materiálov", zväzok 1 "Tlakové potrubia" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
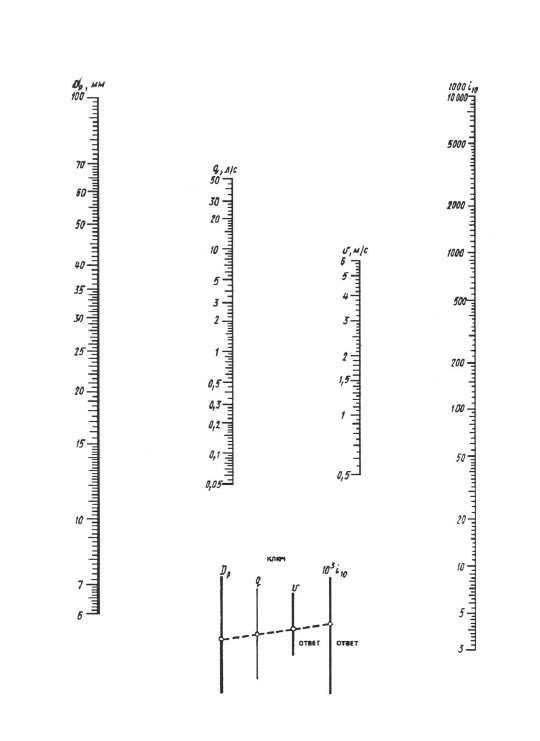
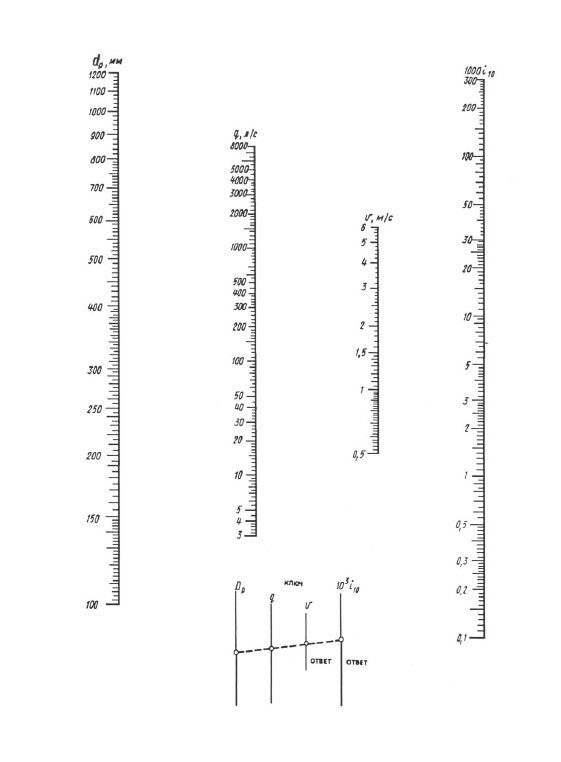
Pri výpočte podľa nomogramov sa výsledok dosiahne jedným prekrytím pravítka - bod s hodnotou vypočítaného priemeru na stupnici dp by ste mali spojiť s bodom s hodnotou vypočítaného prietoku na q (l / s) stupnica s priamkou, pokračujte v tejto priamke, kým sa nepretne so stupnicami rýchlosti V a mernej straty hlavy 1000 i (mm/m). Priesečníky priamky s týmito stupnicami dávajú hodnotu V a 1000 i.
Ako viete, náklady na elektrickú energiu na čerpanie kvapaliny sú priamo úmerné hodnote H (ceteris paribus). Dosadením výrazu (3) do vzorca (2) je ľahké vidieť, že hodnota i (a následne H) je nepriamo úmerná vypočítanému priemeru dp do piateho stupňa.
Vyššie je uvedené, že hodnota dp závisí od hrúbky steny potrubia e: čím je stena tenšia, tým je dp vyššia, a teda tým nižšia je tlaková strata v dôsledku trenia a náklady na elektrickú energiu.
Ak sa z akéhokoľvek dôvodu zmení hodnota MRS potrubia, je potrebné prepočítať jeho priemer a hrúbku steny (SDR).
Treba mať na pamäti, že v mnohých prípadoch použitie rúr s MRS 10 namiesto rúr s MRS 8, najmä rúr s MRS 6.3, umožňuje zmenšiť priemer potrubia o jednu veľkosť. Preto v dnešnej dobe použitie polyetylénu PE 80 (MRS 8) a PE 100 (MRS 10) namiesto polyetylénu PE 63 (MRS 6.3) na výrobu rúr umožňuje nielen znížiť hrúbku steny rúr, ale aj ich hmotnosť. a spotrebu materiálu, ale aj zníženie energetických nákladov na čerpanie kvapaliny (ceteris paribus).
V posledných rokoch (po roku 2013) boli rúry vyrobené z polyetylénu PE80 takmer úplne nahradené z výroby rúrkami vyrobenými z polyetylénu triedy PE100. Vysvetľuje to skutočnosť, že suroviny, z ktorých sú rúry vyrobené, sú dodávané zo zahraničia so značkou PE100.A tiež tým, že polyetylén triedy 100 má viac pevnostných charakteristík, vďaka čomu sa vyrábajú rúry s rovnakými vlastnosťami ako rúry z PE80, ale s tenšou stenou, čím sa zvyšuje priepustnosť polyetylénových potrubí.
Nomogram na určenie tlakových strát v potrubiach s priemerom 6 100 mm.
Nomogram na určenie tlakových strát v potrubiach s priemermi 100, 1200 mm.
Reynoldsovo kritérium
Túto závislosť priniesol anglický fyzik a inžinier Osborne Reynolds (1842-1912).
Kritériom, ktoré pomáha odpovedať na otázku, či je potrebné zvážiť viskozitu, je Reynoldsovo číslo Re. Rovná sa pomeru energie pohybu prvku prúdiacej tekutiny k práci vnútorných trecích síl.
Uvažujme kubický tekutý prvok s dĺžkou hrany n. Kinetická energia prvku je:
Podľa Newtonovho zákona je trecia sila pôsobiaca na tekutý prvok definovaná takto:
Práca tejto sily pri pohybe tekutého prvku na vzdialenosť n je
a pomer kinetickej energie fluidného prvku k práci trecej sily je
Znížime a získame:
Re sa nazýva Reynoldsovo číslo.
Re je teda bezrozmerná veličina, ktorá charakterizuje relatívnu úlohu viskóznych síl.
Napríklad, ak sú rozmery telesa, s ktorým je kvapalina alebo plyn v kontakte, veľmi malé, potom aj pri nízkej viskozite bude Re nevýznamné a prevládajúcu úlohu zohrávajú trecie sily. Naopak, ak sú rozmery telesa a rýchlosť veľké, potom Re >> 1 a dokonca aj veľká viskozita nebude mať takmer žiadny vplyv na charakter pohybu.
Nie vždy veľké Reynoldsove čísla však znamenajú, že viskozita nehrá žiadnu rolu. Takže keď sa dosiahne veľmi veľká (niekoľko desiatok alebo stoviek tisíc) hodnota Re čísla, hladký laminárny (z latinského lamina - „doska“) sa zmení na turbulentný (z latinského turbulentus - „búrlivý“ , „chaotický“), sprevádzané chaotickými, nestabilnými pohybmi tekutín. Tento efekt možno pozorovať, ak postupne otvárate vodovodný kohútik: tenký prúd zvyčajne tečie hladko, ale so zvyšujúcou sa rýchlosťou vody je plynulosť toku narušená. V prúde vytekajúcom pod vysokým tlakom sa častice kvapaliny pohybujú náhodne, oscilujú, všetok pohyb je sprevádzaný silným miešaním.
Výskyt turbulencií výrazne zvyšuje odpor vzduchu. V potrubí je rýchlosť turbulentného prúdenia menšia ako rýchlosť laminárneho prúdenia pri rovnakých poklesoch tlaku. Ale turbulencie nie sú vždy zlé. Vzhľadom na to, že miešanie pri turbulencii je veľmi výrazné, dochádza k prenosu tepla - ochladzovaniu alebo zahrievaniu agregátov oveľa intenzívnejšie; chemické reakcie sa šíria rýchlejšie.
Bernoulliho rovnica stacionárneho pohybu
Jednu z najdôležitejších rovníc hydromechaniky získal v roku 1738 švajčiarsky vedec Daniel Bernoulli (1700-1782). Prvýkrát sa mu podarilo opísať pohyb ideálnej tekutiny vyjadrený Bernoulliho vzorcom.
Ideálna tekutina je tekutina, v ktorej nie sú žiadne trecie sily medzi prvkami ideálnej tekutiny, ako aj medzi ideálnou tekutinou a stenami nádoby.
Rovnica stacionárneho pohybu, ktorá nesie jeho meno, je:
kde P je tlak kvapaliny, ρ je jej hustota, v je rýchlosť pohybu, g je zrýchlenie voľného pádu, h je výška, v ktorej sa prvok kvapaliny nachádza.
Význam Bernoulliho rovnice je, že vo vnútri systému naplneného kvapalinou (úsek potrubia) je celková energia každého bodu vždy nezmenená.
Bernoulliho rovnica má tri pojmy:
- ρ⋅v2/2 - dynamický tlak - kinetická energia na jednotku objemu hnacej kvapaliny;
- ρ⋅g⋅h - hmotnostný tlak - potenciálna energia jednotkového objemu kvapaliny;
- P - statický tlak, vo svojom pôvode je dielom tlakových síl a nepredstavuje rezervu žiadneho špeciálneho druhu energie („tlaková energia“).
Táto rovnica vysvetľuje, prečo sa v úzkych úsekoch potrubia zvyšuje rýchlosť prúdenia a znižuje sa tlak na steny potrubia. Maximálny tlak v potrubí je nastavený presne v mieste, kde má potrubie najväčší prierez. Úzke časti potrubia sú v tomto smere bezpečné, ale tlak v nich môže klesnúť natoľko, že kvapalina vrie, čo môže viesť ku kavitácii a zničeniu materiálu potrubia.
Navier-Stokesova rovnica pre viskózne kvapaliny
V prísnejšej formulácii sa lineárna závislosť viskózneho trenia od zmeny rýchlosti tekutiny nazýva Navier-Stokesova rovnica. Zohľadňuje stlačiteľnosť kvapalín a plynov a na rozdiel od Newtonovho zákona platí nielen v blízkosti povrchu pevného telesa, ale aj v každom bode kvapaliny (pri povrchu pevného telesa v prípade nestlačiteľného kvapalina, Navier-Stokesova rovnica a Newtonov zákon sa zhodujú).
Všetky plyny, pre ktoré je splnená podmienka spojitého média, sa tiež riadia Navier-Stokesovou rovnicou, t.j. sú newtonovské tekutiny.
Viskozita kvapalín a plynov je zvyčajne významná pri relatívne nízkych rýchlostiach, preto sa niekedy hovorí, že Eulerova hydrodynamika je špeciálnym (limitným) prípadom vysokých rýchlostí Navier-Stokesovej hydrodynamiky.
Pri nízkych rýchlostiach, v súlade s Newtonovým zákonom viskózneho trenia, je odporová sila tela úmerná rýchlosti. Pri vysokých rýchlostiach, keď viskozita prestáva hrať významnú úlohu, je odpor telesa úmerný druhej mocnine rýchlosti (čo prvýkrát objavil a doložil Newton).
Hydraulická postupnosť výpočtov
1.
Vyberie sa hlavný obeh
kruhový vykurovací systém (väčšina
nevýhodne umiestnený v hydraulike
vzťah). V slepej dvojtrubke
systémom je prstenec prechádzajúci cez
spodný nástroj najvzdialenejších a
zaťažená stúpačka, v jednorúrkovom -
cez najvzdialenejšie a načítané
stúpačka.
napr.
v dvojrúrkovom vykurovacom systéme s
horná elektroinštalácia hlavná cirkulácia
krúžok prejde z tepelného bodu
cez hlavnú stúpačku, prívodné vedenie,
cez najvzdialenejšiu stúpačku, kúrenie
spotrebič na prízemí, spätné vedenie
do bodu ohrevu.
V
systémy s pridruženým pohybom vody v
prsteň sa považuje za hlavný,
prechádzajú najviac stredom
zaťažený stojan.
2.
Hlavný obehový krúžok sa zlomí
do parciel (zápletka je charakterizovaná
konštantný prietok vody a to isté
priemer). Diagram ukazuje
čísla sekcií, ich dĺžky a term
zaťaženie. Tepelné zaťaženie hlavného
parciel sa určí súčtom
tepelné zaťaženie, ktoré obsluhujú tieto
pozemky. Na výber priemeru potrubia
používajú sa dve množstvá:
a)
daný prietok vody;
b)
približné špecifické tlakové straty
na trenie v konštrukčnom obehu
prsteň RSt.
Pre
kalkulácia Rcp
potrebujete poznať dĺžku hlavného
cirkulačný krúžok a vypočítané
cirkulačný tlak.
3.
Vypočítaný obeh
tlak vzorca
 ,
,
(5.1)
kde
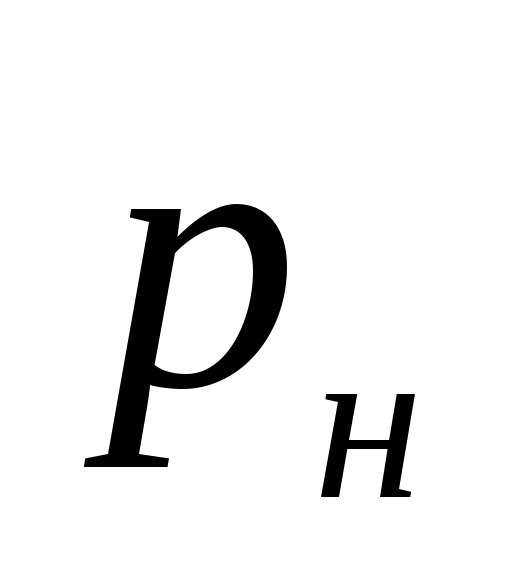
tlak vytvorený čerpadlom, Pa.
Prax pri navrhovaní systému
kúrenie ukázalo, že najviac
odporúča sa odobrať tlak čerpadla,
rovný
 ,
,
(5.2)
kde
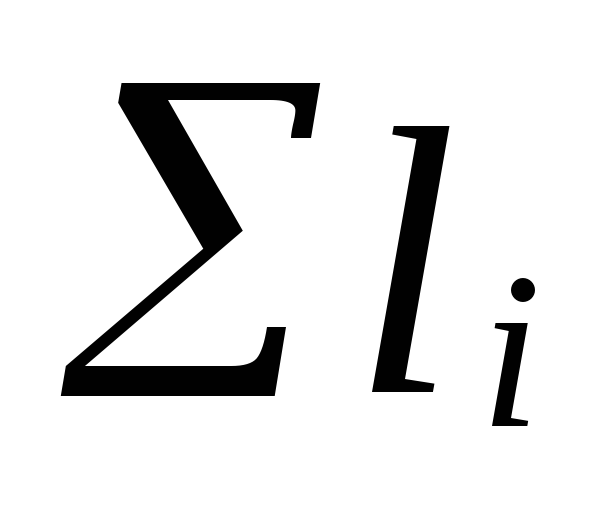
súčet dĺžok úsekov hlavného obehu
prstene;
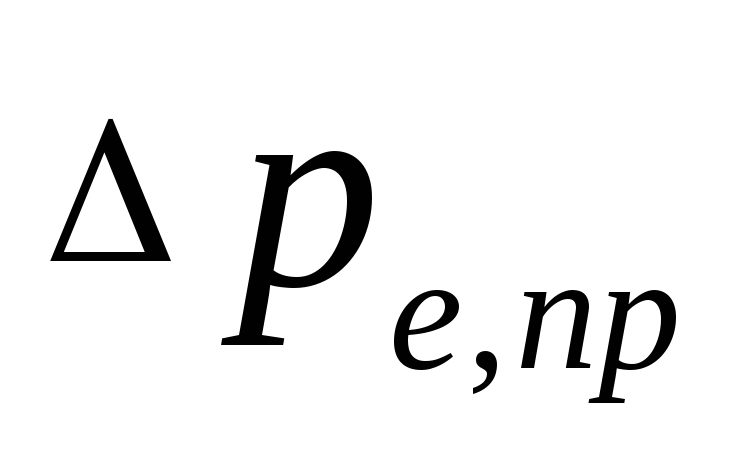
prirodzený tlak, ktorý vzniká, keď
chladenie vodou v spotrebičoch, Pa, možné
určiť ako
 ,
,
(5.3)
kde
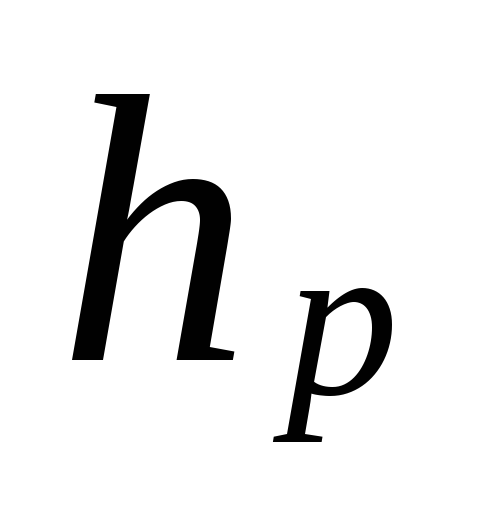
vzdialenosť od stredu pumpy (výťahu)
do stredu zariadenia spodného poschodia, m.
Význam
koeficient možné
určiť z tabuľky 5.1.
tabuľky
5.1 - Význam c
v závislosti od projektovanej teploty
voda vo vykurovacom systéme
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
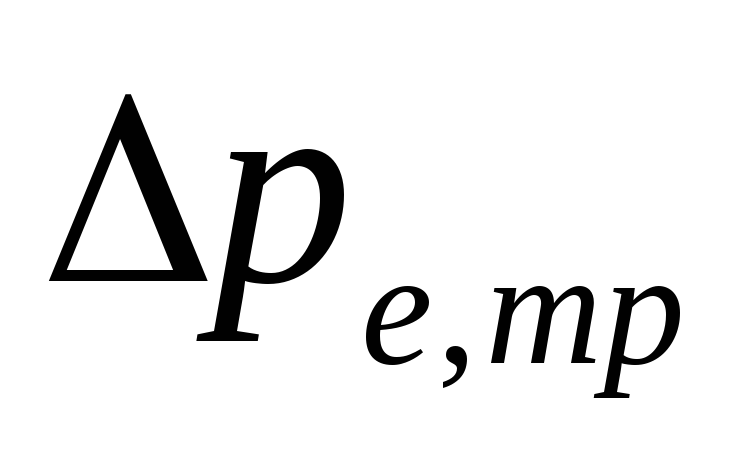
prirodzený tlak v
v dôsledku ochladzovania vody v potrubiach
.
V
čerpacie systémy so spodnou elektroinštaláciou
rozsah
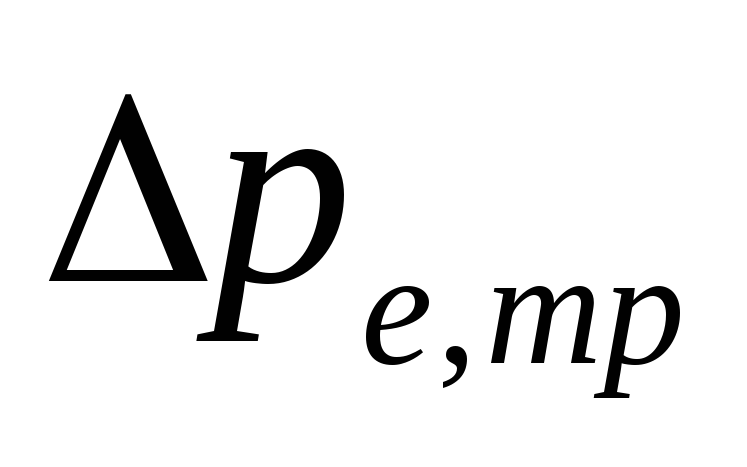
-
Sú určené
špecifická strata tlaku trením
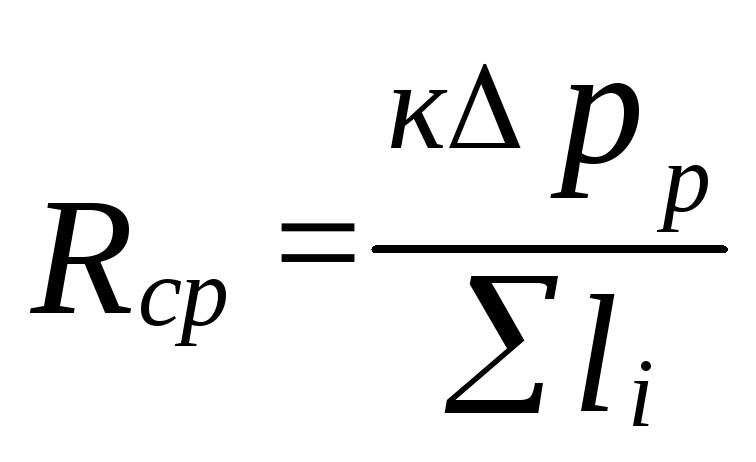
(5.4)
kde
k=0,65 určuje podiel tlakových strát
na trenie.
5.
Prietok vody v oblasti je určený
vzorec
 (5.5)
(5.5)
kde
Q
- tepelná záťaž na mieste, W:
(tG
— tO)
- teplotný rozdiel chladiacej kvapaliny.
6.
Podľa veľkosti
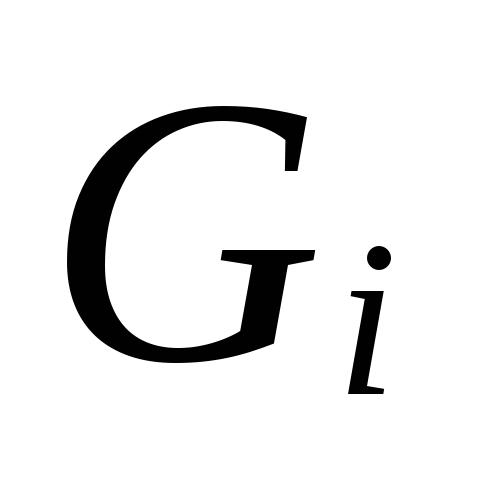
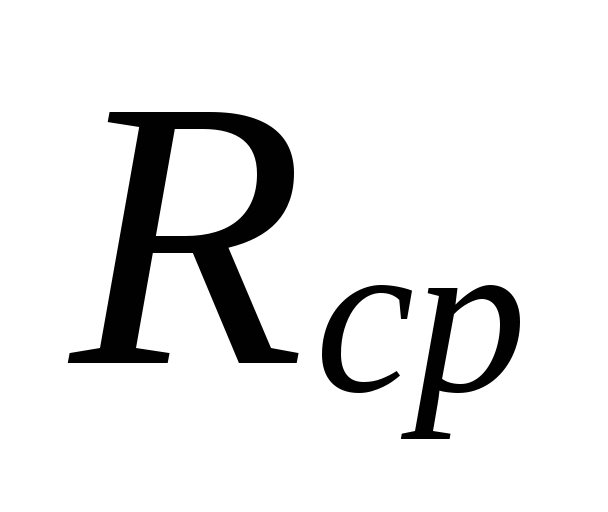
.

6.
Pre vybrané priemery potrubí
a určí sa odhadovaná spotreba vody
rýchlosť chladiacej kvapaliny v
a skutočné špecifiká
strata tlaku trením Rf.
o
výber priemerov v oblastiach s malými
prietoky chladiacej kvapaliny môžu byť
veľké rozdiely medzi
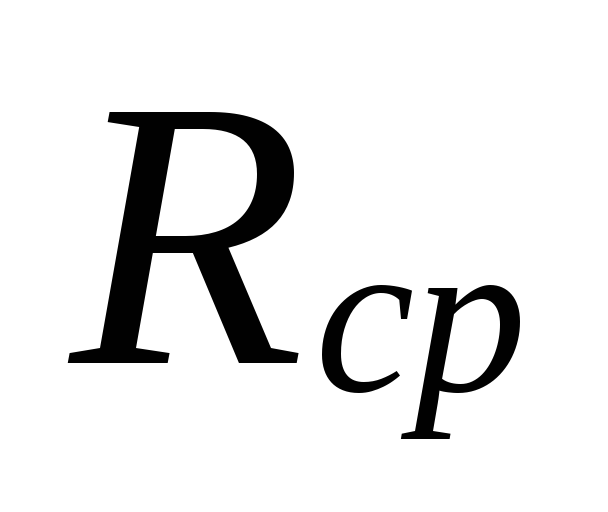
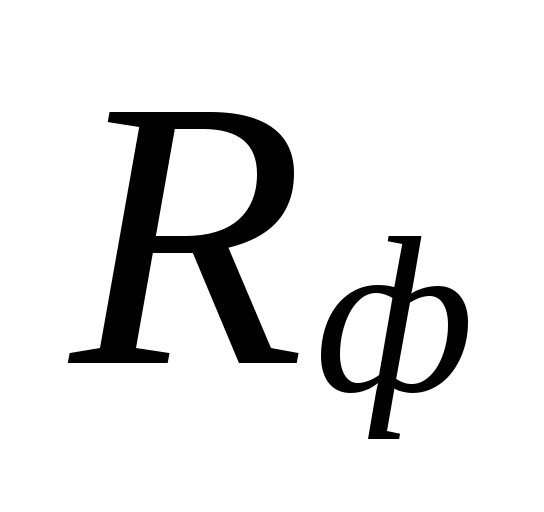
podhodnotené straty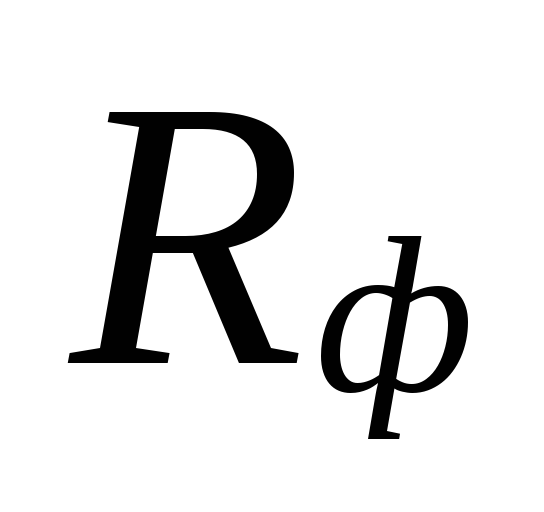
tieto oblasti sú kompenzované nadhodnotením
množstvá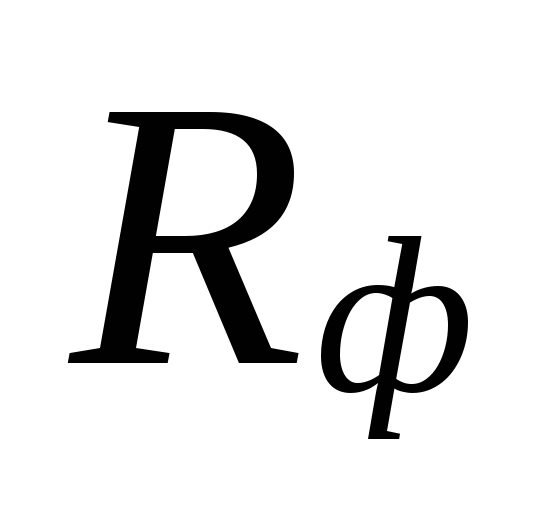
7.
Stanovia sa tlakové straty trením
na vypočítanej ploche, Pa:
 .
.
(5.6)
výsledky
výpočty sú uvedené v tabuľke 5.2.
8.
Straty tlaku v lokálnych
odpory pomocou buď vzorca:
 ,
,
(5.7)
kde
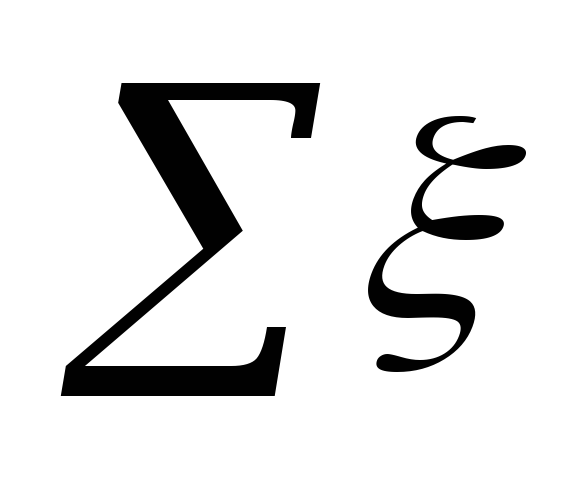
v oblasti osídlenia.
Význam ξ
na každom mieste sú zhrnuté v tabuľke. 5.3.
Tabuľka 5.3 -
Lokálne koeficienty odporu
|
č. p / p |
mená |
hodnoty |
Poznámky |
9.
Určite celkovú tlakovú stratu
v každej oblasti
 .
.
(5.8)
10. Určiť
celková strata tlaku v dôsledku trenia a
v lokálnych odporoch hlavne
obehový krúžok
 .
.
(5.9)
11. Porovnaj Δp
S ΔpR.
Celková strata tlaku v prstenci
musí byť menšia ako ΔpR
na
 .
.
(5.10)
zásoby na jedno použitie
tlak je potrebný na nezohľadnený v
výpočet hydraulického odporu.
Ak nie sú podmienky
sa vykonávajú, je potrebné na niektorých
časti krúžku na zmenu priemerov rúr.
12. Po výpočte
hlavný obehový krúžok
vytvorte spojenie zostávajúcich krúžkov. V
každý nový prsteň sa počíta len
ďalšie neobvyklé oblasti,
zapojené paralelne so sekciami
hlavný krúžok.
Stratový nesúlad
tlaky na paralelne zapojené
pozemky povolené do 15% so slepou uličkou
pohyb vody a až 5% - s prechodom.
tabuľky
5.2 - Výsledky hydraulického výpočtu
pre vykurovací systém
|
Na |
Autor: |
Autor: |
||||||||||||||
|
číslo |
tepelný |
Spotreba |
Dĺžka |
Priemer |
Rýchlosť |
Špecifické |
Straty |
Sum |
Straty |
d, |
v, |
R, |
Δptr, |
∑ξ |
Z, |
Rl+Z, |
Lekcia 6
Zmena teploty plynu pozdĺž dĺžky plynovodu
Pri stacionárnom prúdení plynu hm
prietok v plynovode je
 . (2.41)
. (2.41)
V skutočnosti pohyb plynu v plynovode
je vždy neizotermická. V
Počas kompresie sa plyn zahrieva.
Aj po jeho ochladení na COP sa teplota
plynu vstupujúceho do potrubia
je asi 2040С,
ktorá je oveľa vyššia ako teplota
prostredie (T).
V praxi sa teplota plynu stáva
blízko okolitej teplote
len pre plynovody malého priemeru
(Dy0.
Okrem toho by sa malo vziať do úvahy, že
potrubný plyn
je skutočný plyn, ktorý je neodmysliteľný
Joule-Thompsonov efekt, ktorý berie do úvahy
absorpcia tepla pri expanzii plynu.
Keď sa teplota mení po dĺžke
je opísaný pohyb plynu v plynovode
sústava rovníc:
špecifická energia ,
,
kontinuita ,
,
štátov ,
,
tepelná bilancia .
.
Zvážte v prvom priblížení rovnicu
tepelná bilancia bez zohľadnenia účinku
Joule Thompson. Integrácia rovnice
tepelná bilancia
 ,
,
dostaneme
 , (2.42)
, (2.42)
kde ;
;
KSR- priemer na stránke plný
súčiniteľ prestupu tepla z plynu do
životné prostredie;
G je hmotnostný prietok plynu;
cP–
priemerná izobarická tepelná kapacita plynu.
hodnotutL sa nazýva bezrozmerné kritérium
Šuchov
 (2.43)
(2.43)
Takže teplota plynu na konci
plynovod bude
 . (2.44)
. (2.44)
Vo vzdialenosti x od začiatku
určuje sa teplota plynu v plynovode
podľa vzorca
 . (2.45)
. (2.45)
Zmena teploty pozdĺž dĺžky plynovodu
je exponenciálna (obr.
2.6).
Zvážte
vplyv zmeny teploty plynu na
výkon potrubia.
Vynásobením oboch strán špecifickej rovnice
energie na 2 a vyjadrenie ,
,
dostaneme
 . (2.46)
. (2.46)
Hustotu plynu vyjadrujeme na ľavej strane
výrazov (2.46) zo stavovej rovnice
 ,
,
súčinwz rovnice kontinuity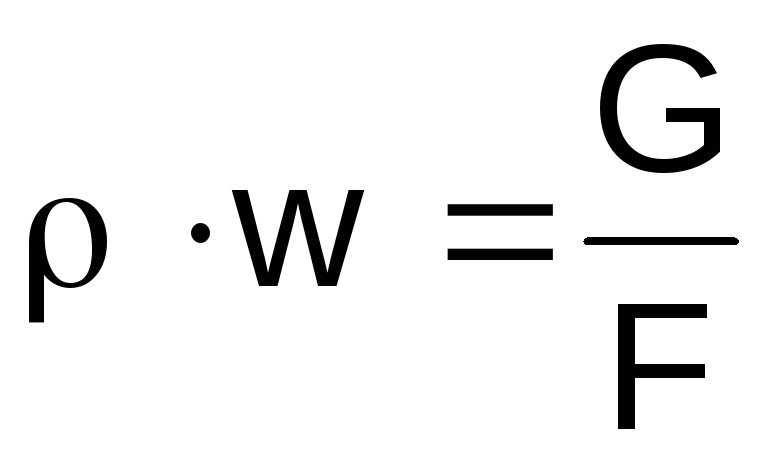
rovnováhu .
.
S ohľadom na túto konkrétnu rovnicu
energia nadobúda formu
 (2.47)
(2.47)
alebo
 . (2.48)
. (2.48)
Označenie
 a integrovanie ľavej strany rovnice
a integrovanie ľavej strany rovnice
(2,48) od PHdoPTOa vpravo od THdoTTO, dostaneme
 . (2.49)
. (2.49)
Nahradením
 , (2.50)
, (2.50)
máme
 . (2.51)
. (2.51)
Po integrácii v špecifikovanom
limity, dostaneme

 . (2.52)
. (2.52)
Berúc do úvahy (2.42)

alebo
 , (2.53)
, (2.53)
kde je korekčný faktor, ktorý zohľadňuje
je korekčný faktor, ktorý zohľadňuje
zmena teploty pozdĺž dĺžky plynovodu
(neizotermia prúdu plynu).
Berúc do úvahy (2.53), závislosť na urč
hmotnostný prietok plynu bude mať tvar
 . (2.54)
. (2.54)
Hodnota Hvždy väčšia ako jedna, takže
hmotnostný prietok plynu pri zmene
teplota pozdĺž dĺžky plynovodu
(neizotermický režim prúdenia) vždy
menej ako v izotermickom režime
(T=idem). Produkt THsa nazýva stredný integrál
teplota plynu v potrubí.
S hodnotami Shukhovho čísla Shu4
prietok plynu v potrubí
považovať za takmer izotermické
pri T=tamtiež. Taká teplota
režim je možný pri čerpaní plynu s
nízke náklady na plynovod
malý (menej ako 500 mm) priemer na významný
vzdialenosť.
Vplyv zmeny teploty plynu
prejavuje sa pre hodnoty Shukhovho čísla
Shu
o
čerpanie plynu prítomnosť škrtiacej klapky
účinok vedie k hlbšiemu
chladenie plynu než len s výmenou tepla
s pôdou. V tomto prípade teplota
plyn môže dokonca klesnúť nižšie
teplota T (obr.
2.7).
Ryža. 2.7. Vplyv Joule-Thompsonovho efektu
na rozdelení teploty plynu nad
dĺžka potrubia
1 - bez zohľadnenia Di; 2 - s
berúc do úvahy Di
Potom, berúc do úvahy Joule-Thompsonov koeficient
zákon zmeny teploty pozdĺž dĺžky
má formu
 , (2.55)
, (2.55)
5 Hydraulické straty
Rozdiel
tlak oleja v dvoch sekciách jednej
a to isté potrubie za predpokladu, že
prvý sa nachádza proti prúdu a
druhý - nižšie, je určený rovnica
Bernoulli
 ,
,
kde
h2
– h1
- rozdiel vo výškach ťažísk
sekcií z ľubovoľne zvoleného
horizontálna úroveň;
v1,
v2
– priemerné rýchlosti oleja v úsekoch;
g - zrýchlenie sily
gravitácia;

hydraulické straty počas pohybu
oleje z prvej sekcie do druhej.
Rovnica
Bernoulli v plnom využití
pre výpočet sacích potrubí čerpadiel;
v ostatných prípadoch prvý termín,
zvyčajne zanedbávané a považované za:

hydraulické
straty sa zvyčajne delia na lokálne
straty a straty trením po dĺžke
potrubia (lineárne).
1.5.1
lokálne straty
energie sú spôsobené miestnymi
hydraulický odpor,
spôsobujúce skreslenie toku. Miestne
odpory sú: zúženia,
rozšírenie, zaoblenie potrubí,
filtre, ovládacie zariadenia a
regulácia a pod.Pri prúdení
kvapaliny cez miestne odpory
jeho rýchlosť sa mení a zvyčajne existujú
veľké víry.
Straty
tlak z miestnych odporov
určený vzorcom Weisbach:
 MPa
MPa
(alebo
 pa),
pa),
kde

strata,
v
je priemerná rýchlosť prúdenia cez prierez
v potrubí za lokálnym odporom, m/s;
,
N/m3;
g = 9,81 m/s2.
Každý
je charakterizovaná lokálna rezistencia
hodnotou jeho koeficientu

Pri turbulentnom prúdení sú hodnoty
odpor a meniť len veľmi málo
so zmenou veľkosti úseku, rýchlosti
prietok tekutiny a viskozita. Takže
predpokladať, že nezávisia od počtu
Reynolds Re.
hodnoty

napríklad pre odpaliská s tým istým
priemery kanálov sa berú rovnaké,
ak:
tokov
sčítať, rozchádzať sa; prúdiť
absolvovanie;









pri
ohyb potrubia

hodnoty

v hydraulických systémoch zariadení, prevzatých z
referenčná literatúra.
o
laminárne prúdenie (Re
Straty
tlak z miestnych odporov pri
laminárne prúdenie sú určené
vzorec:
 MPa
MPa
kde

= a

množstvá
tlaková strata v norme
hydraulické zariadenia pre
nominálny prietok zvyčajne
uvedené v ich technických špecifikáciách.
1.5.2
Strata na
dĺžkové trenie
je strata energie, ku ktorej dochádza
v priamych rúrach s konštantným prierezom,
tie. s rovnomerným prietokom tekutiny,
a zväčšovať úmerne k dĺžke
potrubia. Tieto straty sú spôsobené internými
trenie v kvapaline, a preto majú
vložte do hrubých aj hladkých rúr.
Straty
trecí tlak potrubia
sa určuje podľa vzorca Darcy:
 MPa
MPa
kde

l
a d
- dĺžka a vnútorný priemer potrubia,
mm.
Toto
vzorec je použiteľný pre laminárne,
ako aj pri turbulentnom prúdení; rozdiel
spočíva len v hodnotách koeficientu

o
laminárne prúdenie (Re
o
turbulentný prietokový koeficient trenia
nie je len funkciou Re, ale
závisí aj od drsnosti vnútrajška
povrch potrubia. Pre hydraulicky
hladká potrubia,
tie. s drsnosťou, že
prakticky neovplyvňuje jeho odolnosť,
koeficient turbulentného trenia
režim možno určiť podľa vzorca PC.
Konáková:

rúra
sa považuje za hydraulicky hladký, ak
(d/k)>(Re/20),
kde k je ekvivalentná drsnosť,
mm. Napríklad pre novú bezšvíkovú oceľ
potrubia k≈0,03
mm a po niekoľkých rokoch prevádzky
k≈0,2
mm, pre nové bezšvíkové rúry z
neželezné kovy k≈0,005
mm. Tieto potrubia sa často používajú v
hydraulické systémy obrábacích strojov.
Koeficient
trenie v turbulentnom režime môže byť
určiť podľa vzorca Altshulya,
byť univerzálny (t. j. použiteľný
v každom prípade):

2. Prietokové charakteristiky potrubného prietokového modulu
Spomeňme si
lineárny stratový vzorec - Darcyho vzorec
- Weisbach:
 .
.
expresné
v tomto vzorci rýchlosť V
cez tok Q
z pomeru
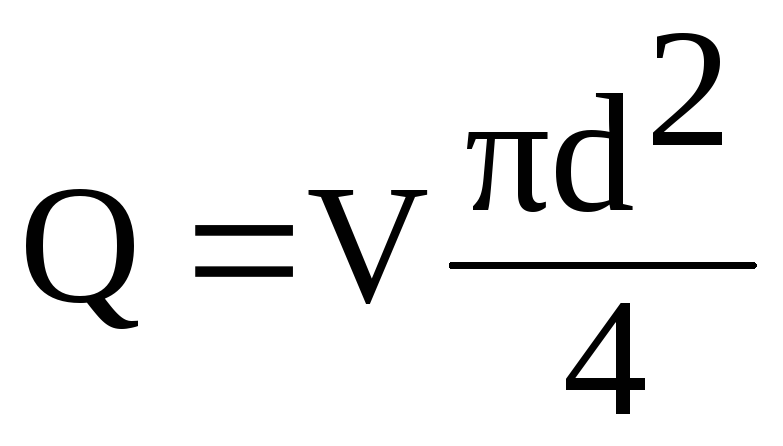
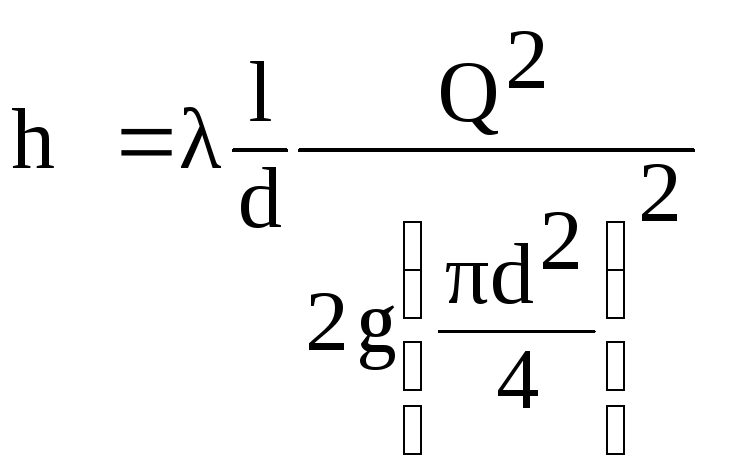
(6.1)
Pre
potrubie určitého priemeru
komplex veličín
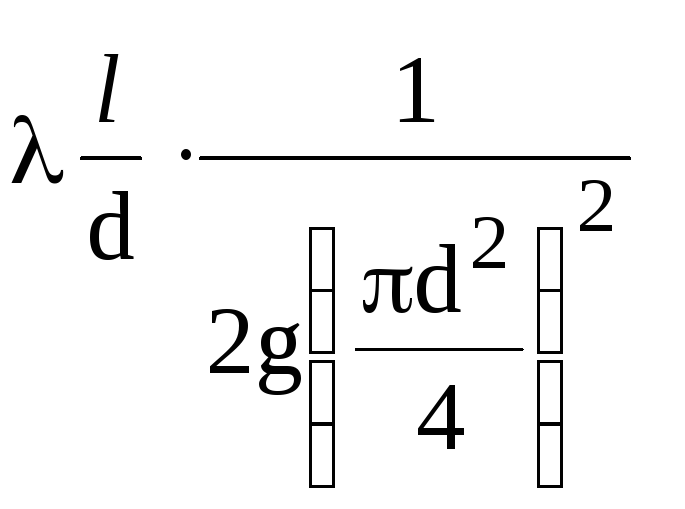
konštanta (1/K2),
okrem hydraulického koeficientu
trenie λ. Na základe konceptu
priemerná ekonomická rýchlosť Vnapr
ukážme, že uvedený koeficient λ
možno pripísať tomuto komplexu, pretože v
V tomto prípade bude Reynoldsovo číslo
majú konkrétny význam:
 ,
,
a na Nikuradzeho grafe koeficient λ in
tento prípad bude mať špecifický
význam.
odôvodniť
oprávnenosť zavedenia koncepcie
priemerná ekonomická rýchlosť nasledovne
uvažovanie.
hydraulické
systém, ako je vodovod,
môžete preskočiť určitý výdavok
vyrobené z rúrok rôznych priemerov. o
Súčasne so zväčšením priemeru d,
preto pokles rýchlosti V
kapitálové výdavky vzrastú a
prevádzkové náklady budú
pokles v dôsledku poklesu hydrauliky
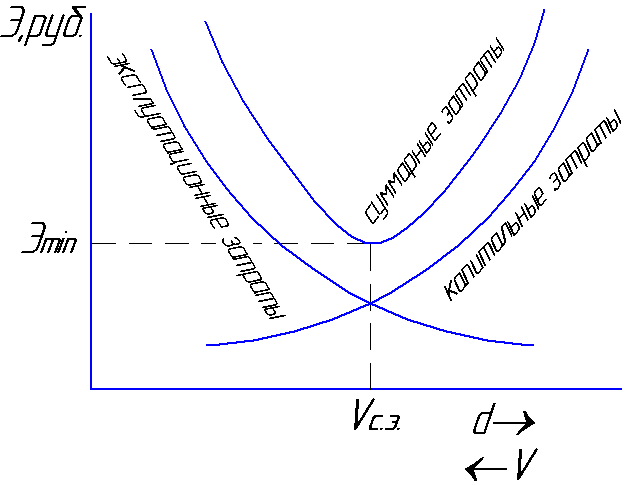
straty. Rýchlosť, pri ktorej súčet
náklady budú minimálne
sa bude nazývať priemerná ekonomická
rýchlosť Vnapr
= 0,8 ... 1,3 m / s (obr. 6.1).
obr.6.1
Potom
vzorec lineárnej straty (6.1) má formu
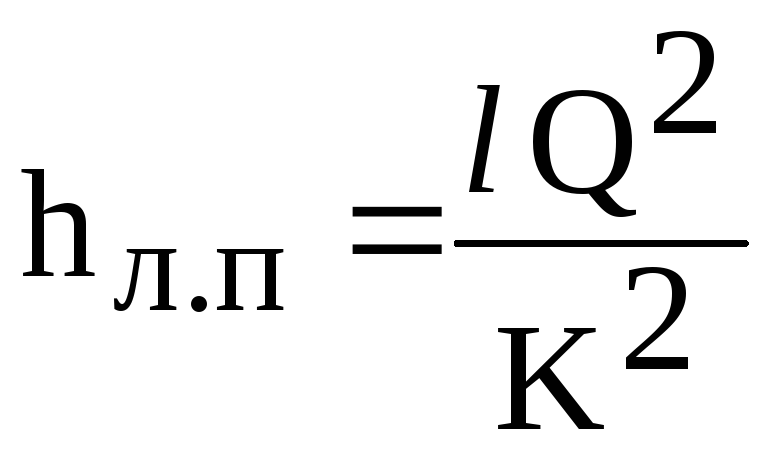
(6.2)
kde
K - prietoková charakteristika potrubia
(modul toku), v závislosti od materiálu
potrubie, priemer a prietok. je zabraný
zo stolov.
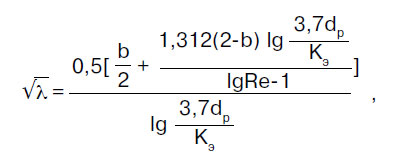
 ), C
), C ,
,