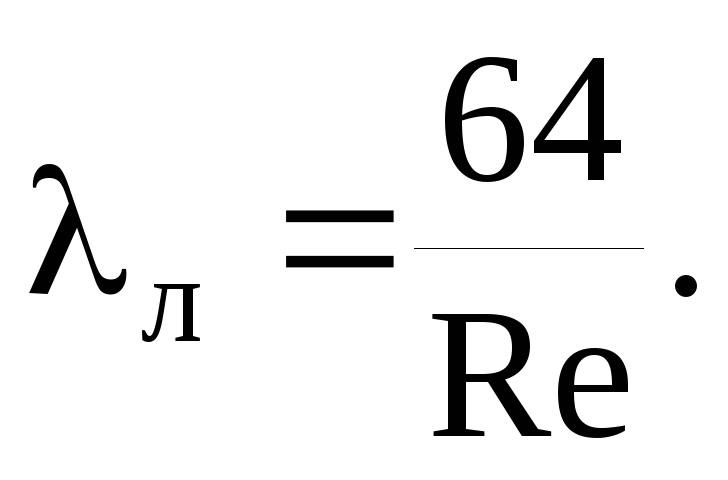1. Hydrostatiskt tryck
Hydrostatiskt tryck är
inre tryckkraft pga
genom inverkan av yttre krafter som appliceras på
given punkt i vätskan. Sådan press
i alla riktningar är densamma och beror
på positionen för en punkt i en vätska i vila.
Dimension av hydrostatiskt tryck
i MKGSS-systemet - kg / cm2 eller t / m2,
i SI-systemet - N/m2.
Grundläggande enhetsförhållanden
tryck:
|
kg/cm2 |
N/m2 |
|
|
teknisk atmosfär |
1 |
98066,5 |
|
millimeter vattenpelare |
0,0001 |
9,80665 |
|
millimeter kvicksilver |
0,00136 |
133,32 |
I praktiska beräkningar, 1 teknisk
atmosfär \u003d 1 kg / cm2 \u003d 10 m vatten. Konst. =
735 mmHg Konst. = 98070 N/m2.
För en inkompressibel vätska alltså
i balans under kraft
gravitation, full hydrostatisk
punkttryck:
p=p+

där p är trycket på den fria
vätskeyta;

höjd h med area
tvärsnitt lika med ett;
h - nedsänkningsdjup
poäng;

För vissa vätskor, värdena
specifik vikt som används för att lösa
uppgifterna finns i bilagan (tab.
P-3).
Värdet av övertryck över
atmosfärisk (sa)
kallas manometrisk, eller
övertryck:

Om trycket på den fria ytan
lika med atmosfäriskt, sedan överskott
tryck sidm=

Underatmosfäriskt tryck
kvantiteten kallas vakuum:
Rwack= sida- R.
Lösningen på de flesta av problemen med detta
avsnitt är relaterat till användningen
den grundläggande ekvationen för hydrostatik

där z är koordinaten eller
punktmärke.
1. Allmän information om hydraulisk beräkning av rörledningar
Vid beräkning
rörledningar övervägs
jämnt, jämnt tryck
rörelse av någon vätska
turbulent regim, i rundcylindrisk
rör. Vätska i tryckrör
är under press och
deras tvärsnitt är helt
fylld. Rörelsen av vätska längs
pipeline uppstår som ett resultat
det faktum att trycket i början av det är större än
i slutet.
Hydraulisk
beräkningen görs för att fastställa
rörledningens diameter d
med en känd
längd för att säkerställa överhoppning
ett visst flöde F
eller upprättande
vid en given diameter och längd av den önskade
tryck och vätskeflöde. Rörledningar
beroende på deras längd och mönster
platser är indelade i enkla
och komplex. Till enkla pipelines
inkluderar rörledningar som inte har
grenar längs längden, med en konstant
samma kostnad.
Rörledningar
består av rör med samma diameter
längs hela längden eller från sektioner av rör av olika
diametrar och längder. Sista fallet
hänvisar till en seriell anslutning.
Enkla pipelines
beroende på längden med en tomt av lokala
motstånd är indelade i korta och
lång. kort
rörledningar
är
rörledningar med tillräckligt kort längd,
där lokalt motstånd
utgör mer än 10 % av hydrauliken
längdförlust. Till exempel inkluderar de:
sifonrör, sug
rör av skovelpumpar, sifoner (tryck
vattenledningar under vägvallen),
rörledningar inuti byggnader och strukturer
etc.
lång
rörledningar
kallad
rörledningarna är relativt stora
längder där huvudet tappar längs längden
betydligt fler än lokalt
förluster. Lokala förluster är
mindre än 5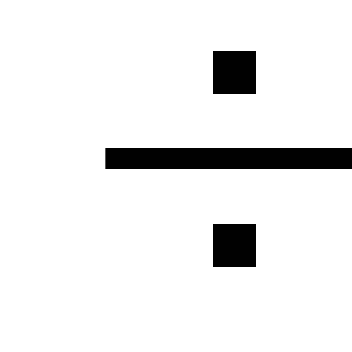
förluster längs rörledningens längd, och därför
de kan försummas eller introduceras på
hydrauliska beräkningar ökar
koefficient lika med 1,05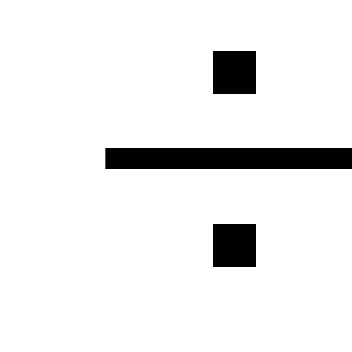
Långa rörledningar kommer in i systemet
vattenförsörjningsnät, pumpledningar
stationer, ledningar och rörledningar
industriföretag och
jordbruksändamål och
etc.
Komplexa rörledningar
har olika grenar längs längden,
de där. rörledningen består av ett nätverk av rör
vissa diametrar och längder. Komplex
rörledningar är indelade i
parallell, återvändsgränd (grenad),
ring (slutna) rörledningar,
ingår i vattenledningsnätet.
Hydraulisk
rörledningsberäkning minskas som
vanligtvis för att lösa tre huvudproblem:
-
definition
rörledningsflöde F,
om känt
tryck H,
längd l
och diameter d
rörledning,
med tanke på tillgängligheten av vissa lokala
motstånd eller i deras frånvaro; -
definition
erforderligt tryck H,
nödvändigt för att säkra ett pass
känt flöde F
med pipeline
lång l
och diameter d; -
definition
rörledningens diameter d
när
kända huvudvärden H,
bekostnad F
och längd l.
Vätskeflödeshastigheten är
där q > beräknat vätskeflöde, m3/s;
- arean av rörets strömförande sektion, m2.
Friktionsmotståndskoefficienten λ bestäms i enlighet med reglerna i regeluppsättningen SP 40-102-2000 "Design och installation av rörledningar för vattenförsörjning och avloppssystem gjorda av polymera material. Allmänna krav":
där b är något likhetsantal för vätskeflödesregimer; för b > 2 tas b = 2.
där Re är det faktiska Reynolds-talet.
där ν är koefficienten för vätskans kinematiska viskositet, m²/s. Vid beräkning av kallvattenrör tas det lika med 1,31 10-6 m² / s - vattnets viskositet vid en temperatur av +10 ° C;
Rekv > - Reynolds nummer som motsvarar början av den kvadratiska regionen av hydrauliskt motstånd.
där Ke är rörmaterialets hydrauliska grovhet, m. För rör av polymermaterial tas Ke = 0,00002 m om rörtillverkaren inte anger andra grovhetsvärden.
I de fall av flöde när Re ≥ Rekv, blir det beräknade värdet av parametern b lika med 2, och formel (4) förenklas avsevärt och blir till den välkända Prandtl-formeln:
Vid Ke = 0,00002 m uppträder det kvadratiska motståndsområdet vid en vattenflödeshastighet (ν = 1,31 10-6 m²/s) lika med 32,75 m/s, vilket är praktiskt taget ouppnåeligt i allmänna vattenförsörjningssystem.
För vardagliga beräkningar rekommenderas nomogram, och för mer exakta beräkningar - "Tabell för hydrauliska beräkningar av rörledningar gjorda av polymera material", volym 1 "Tryckrörledningar" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
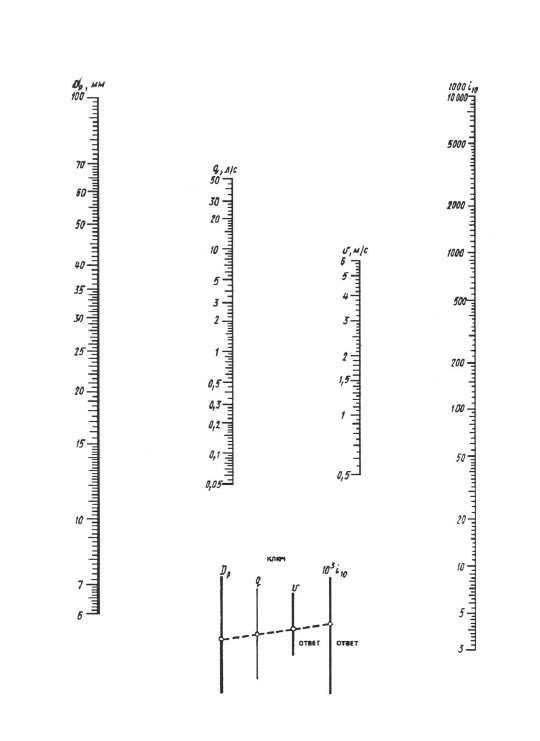
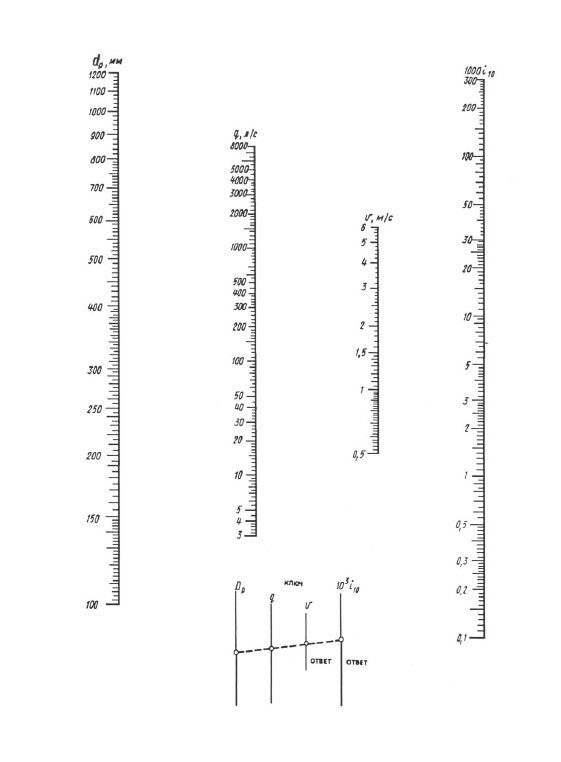
Vid beräkning enligt nomogram uppnås resultatet av en överlagring av linjalen - du bör ansluta punkten med värdet av den beräknade diametern på dp-skalan med punkten med värdet av den beräknade flödeshastigheten på q (l / s) skala med en rät linje, fortsätt denna räta linje tills den skär skalorna för hastighet V och specifika förluster huvud 1000 i (mm/m). Skärningspunkterna för en rät linje med dessa skalor ger värdet V och 1000 i.
Som ni vet är kostnaden för elektricitet för att pumpa vätska direkt proportionell mot värdet på H (ceteris paribus). Genom att ersätta uttrycket ( 3 ) i formeln ( 2 ), är det lätt att se att värdet av i (och följaktligen H) är omvänt proportionell mot den beräknade diametern dp till femte graden.
Det visas ovan att värdet på dp beror på tjockleken på rörväggen e: ju tunnare väggen är, desto högre dp och följaktligen desto lägre tryckförlust på grund av friktion och kostnaden för el.
Om rörets MRS-värde ändras av någon anledning måste dess diameter och väggtjocklek (SDR) beräknas om.
Man bör komma ihåg att användningen av rör med MRS 10 istället för rör med MRS 8, särskilt rör med MRS 6.3, i ett antal fall gör det möjligt att minska rörledningens diameter med en storlek. Därför, i vår tid, tillåter användningen av polyeten PE 80 (MRS 8) och PE 100 (MRS 10) istället för polyeten PE 63 (MRS 6.3) för tillverkning av rör inte bara att minska rörens väggtjocklek, deras vikt och materialförbrukning, men också för att minska energikostnaderna för pumpning av vätska (ceteris paribus).
Under de senaste åren (efter 2013) har rör tillverkade av PE80 polyeten nästan helt ersatts från produktionen av rör tillverkade av PE100 polyeten. Detta förklaras av att råvarorna som rören är tillverkade av levereras från utlandet med märket PE100.Och även av det faktum att polyeten 100-kvalitet har fler hållfasthetsegenskaper, på grund av vilka rör produceras med samma egenskaper som rör av PE80, men med en tunnare vägg, vilket ökar genomströmningen av polyetenrörledningar.
Nomogram för bestämning av tryckförluster i rör med diameter 6 100 mm.
Nomogram för bestämning av tryckförluster i rör med diametrar 100, 1200 mm.
Reynolds kriterium
Detta beroende togs fram av den engelske fysikern och ingenjören Osborne Reynolds (1842-1912).
Kriteriet som hjälper till att svara på frågan om det finns ett behov av att överväga viskositet är Reynolds-talet Re. Det är lika med förhållandet mellan rörelseenergin för ett element i en strömmande vätska och arbetet med interna friktionskrafter.
Betrakta ett kubiskt vätskeelement med kantlängd n. Den kinetiska energin för ett element är:
Enligt Newtons lag definieras friktionskraften som verkar på ett flytande element enligt följande:
Verkan av denna kraft när ett flytande element flyttas över ett avstånd n är
och förhållandet mellan fluidelementets kinetiska energi och friktionskraftens arbete är
Vi minskar och får:
Re kallas Reynolds-numret.
Således är Re en dimensionslös storhet som kännetecknar den relativa rollen av viskösa krafter.
Till exempel, om dimensionerna på kroppen som vätskan eller gasen är i kontakt med är mycket små, kommer Re även med en låg viskositet att vara obetydlig och friktionskrafter spelar en dominerande roll. Tvärtom, om kroppens dimensioner och hastigheten är stora, kommer Re >> 1 och även en hög viskositet att ha nästan ingen effekt på rörelsens natur.
Men inte alltid stora Reynolds-tal betyder att viskositeten inte spelar någon roll. Så när ett mycket stort (flera tiotals eller hundratusentals) värde av Re-talet uppnås, förvandlas ett jämnt laminärt (från latinets lamina - "platta") flöde till ett turbulent (från latinets turbulentus - "stormigt" , "kaotisk"), åtföljd av kaotiska, ostadiga rörelser vätskor. Denna effekt kan observeras om du gradvis öppnar en vattenkran: en tunn ström flyter vanligtvis smidigt, men med en ökning av vattnets hastighet störs flödets jämnhet. I en stråle som strömmar ut under högt tryck, rör sig flytande partiklar slumpmässigt, oscillerande, all rörelse åtföljs av kraftig blandning.
Uppkomsten av turbulens ökar kraftigt motståndet. I en rörledning är den turbulenta flödeshastigheten mindre än den laminära flödeshastigheten vid samma tryckfall. Men turbulens är inte alltid dåligt. På grund av det faktum att blandning under turbulens är mycket betydande, sker värmeöverföring - kylning eller uppvärmning av aggregat - mycket mer intensivt; kemiska reaktioner sprids snabbare.
Bernoullis ekvation för stationär rörelse
En av hydromekanikens viktigaste ekvationer erhölls 1738 av den schweiziska vetenskapsmannen Daniel Bernoulli (1700-1782). Han lyckades först beskriva rörelsen hos en ideal vätska, uttryckt i Bernoullis formel.
En ideal vätska är en vätska i vilken det inte finns några friktionskrafter mellan elementen i en ideal vätska, såväl som mellan den ideala vätskan och kärlets väggar.
Ekvationen för stationär rörelse som bär hans namn är:
där P är vätskans tryck, ρ är dess densitet, v är rörelsehastigheten, g är accelerationen av fritt fall, h är höjden på vilken vätskans element är beläget.
Innebörden av Bernoullis ekvation är att inuti ett system fyllt med vätska (rörledningssektion) är den totala energin för varje punkt alltid oförändrad.
Bernoullis ekvation har tre termer:
- ρ⋅v2/2 - dynamiskt tryck - kinetisk energi per volymenhet av drivvätskan;
- ρ⋅g⋅h - vikttryck - potentiell energi per volymenhet vätska;
- P - statiskt tryck, i sitt ursprung är tryckkrafternas arbete och representerar inte en reserv av någon speciell typ av energi ("tryckenergi").
Denna ekvation förklarar varför i smala delar av röret flödeshastigheten ökar och trycket på rörväggarna minskar. Maxtrycket i rören ställs in exakt på den plats där röret har störst tvärsnitt. Smala delar av röret är säkra i detta avseende, men trycket i dem kan sjunka så mycket att vätskan kokar, vilket kan leda till kavitation och förstörelse av rörmaterialet.
Navier-Stokes ekvation för trögflytande vätskor
I en mer rigorös formulering kallas det linjära beroendet av viskös friktion på förändringen i vätskehastigheten Navier-Stokes ekvation. Den tar hänsyn till vätskors och gasers kompressibilitet och är, till skillnad från Newtons lag, giltig inte bara nära ytan av en fast kropp, utan också vid varje punkt i vätskan (nära ytan av en fast kropp i fallet med en inkompressibel kropp vätska, Navier-Stokes ekvation och Newtons lag sammanfaller).
Alla gaser för vilka villkoret för ett kontinuerligt medium är uppfyllt följer också Navier-Stokes ekvation, dvs. är newtonska vätskor.
Viskositeten för vätskor och gaser är vanligtvis signifikant vid relativt låga hastigheter, därför sägs det ibland att Euler hydrodynamik är ett speciellt (begränsande) fall av höga hastigheter av Navier-Stokes hydrodynamik.
Vid låga hastigheter, i enlighet med Newtons lag om viskös friktion, är kroppens dragkraft proportionell mot hastigheten. Vid höga hastigheter, när viskositeten upphör att spela en betydande roll, är kroppens motstånd proportionell mot kvadraten på hastigheten (som först upptäcktes och underbyggdes av Newton).
Hydraulisk beräkningssekvens
1.
Huvudcirkulationen är vald
ringvärmesystem (de flesta
ofördelaktigt placerad i hydrauliken
relation). I återvändsgränd tvårör
system är en ring som passerar igenom
lägre instrument av de mest avlägsna och
laddat stigrör, i enkelrör -
genom den mest avlägsna och laddade
stigare.
Till exempel,
i ett tvårörs värmesystem med
övre ledningshuvudcirkulationen
ringen kommer att passera från värmepunkten
genom huvudstigröret, matningsledningen,
genom den mest avlägsna stigaren, uppvärmning
nedervåningen apparat, returledning
till värmepunkten.
V
system med tillhörande vattenrörelse in
ringen tas som den viktigaste,
går genom mitten mest
laddat stativ.
2.
Huvudcirkulationsringen går sönder
till tomter (tomten karakteriseras
konstant vattenflöde och detsamma
diameter). Diagrammet visar
sektionsnummer, deras längder och termiska egenskaper
massor. Termisk belastning av huvudledningen
tomter bestäms genom summering
termiska belastningar som betjänas av dessa
tomter. För att välja rördiameter
två kvantiteter används:
a)
givet vattenflöde;
b)
ungefärliga specifika tryckförluster
för friktion i designcirkulationen
ringa Rons.
För
beräkning Rcp
behöver veta längden på huvudet
cirkulationsring och beräknas
cirkulationstryck.
3.
Den beräknade cirkulationen
formeltryck
 ,
,
(5.1)
var
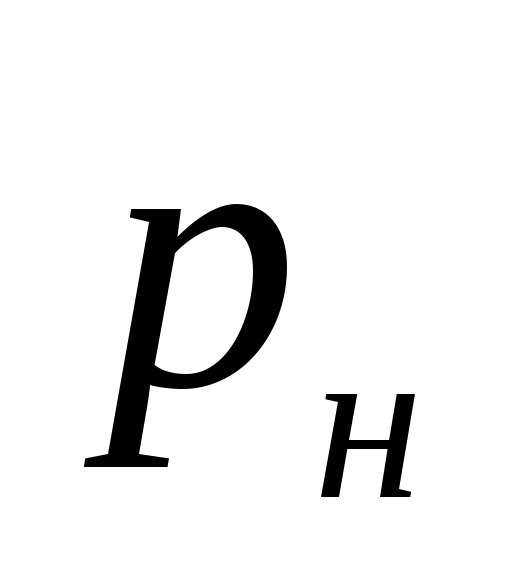
tryck som skapas av pumpen, Pa.
System Design Practice
uppvärmning visade att den mest
det är tillrådligt att ta pumpens tryck,
likvärdig
 ,
,
(5.2)
var
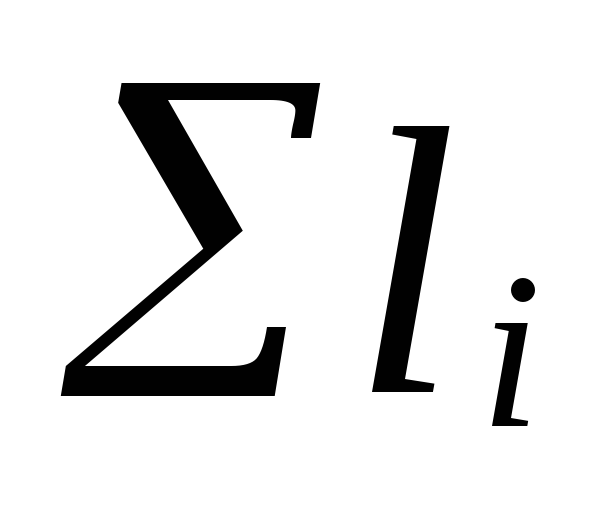
summan av längderna av huvudcirkulationens sektioner
ringar;
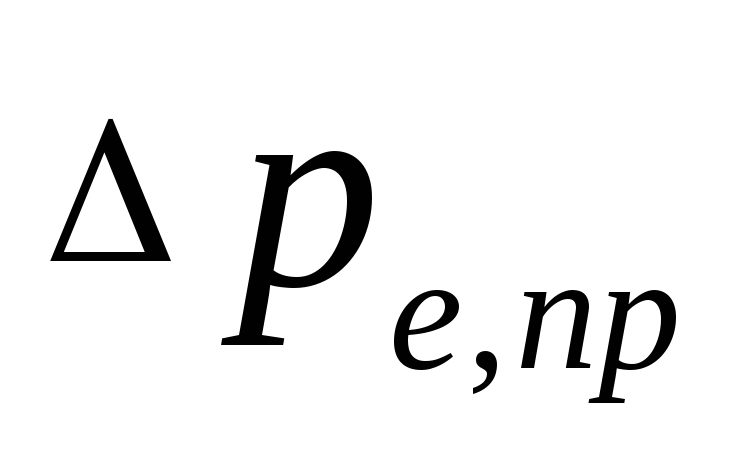
naturligt tryck som uppstår när
vattenkylning i apparater, Pa, möjligt
avgöra hur
 ,
,
(5.3)
var
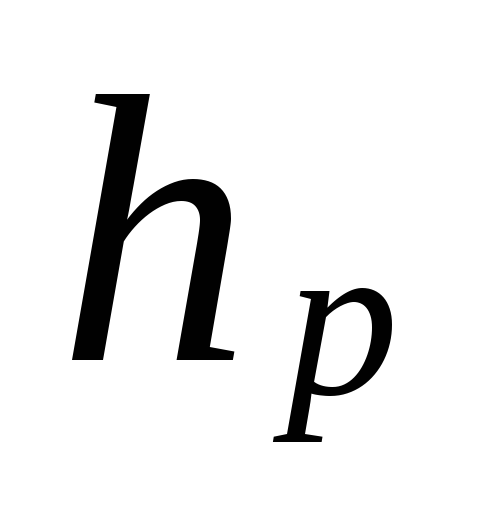
avstånd från pumpens centrum (hiss)
till mitten av enheten på nedre våningen, m.
Menande
koefficient möjligt
avgöra från tabell 5.1.
tabell
5.1 - Betydelse c
beroende på designtemperaturen
vatten i värmesystemet
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
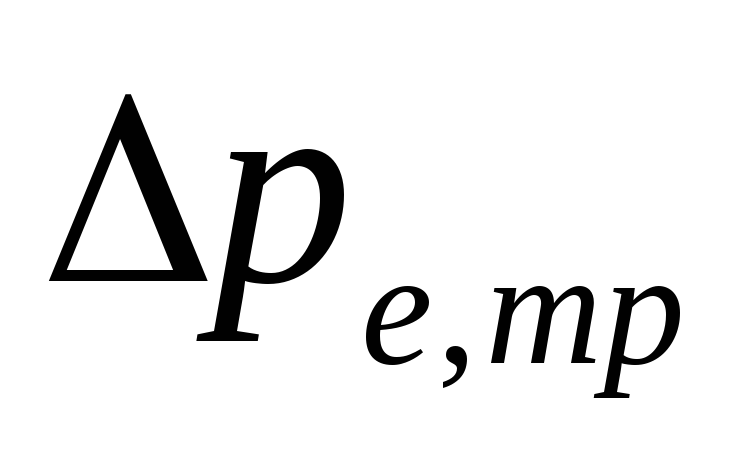
naturligt tryck in
till följd av vattenkylning i rörledningar
.
V
pumpsystem med bottenledningar
magnitud
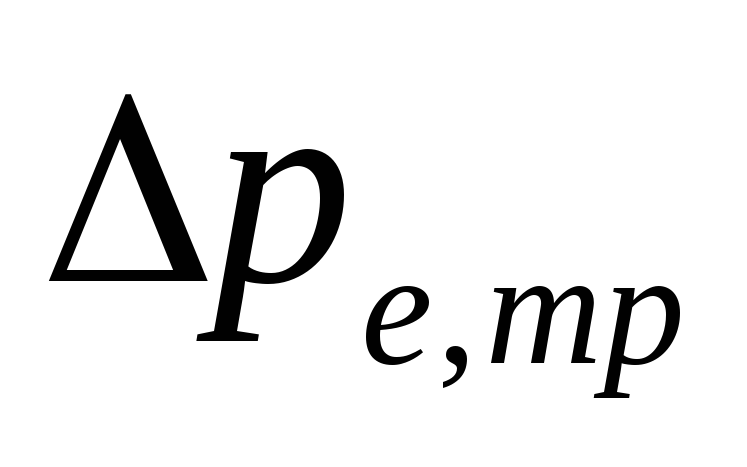
-
är bestämda
specifik friktionstrycksförlust
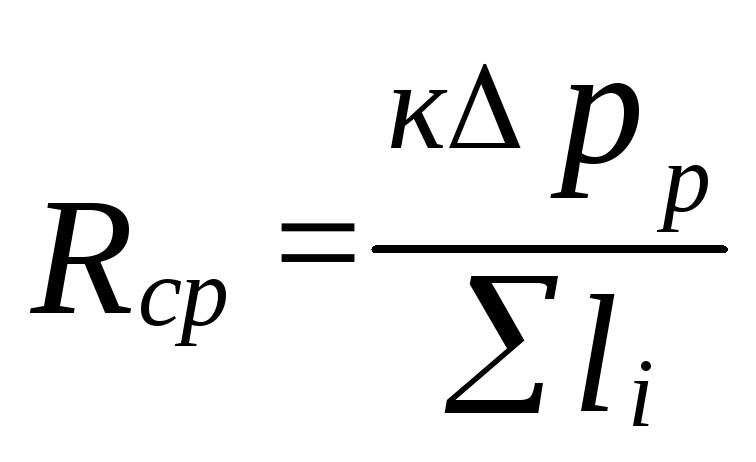
(5.4)
var
k=0,65 bestämmer andelen tryckförluster
för friktion.
5.
Vattenförbrukningen på platsen bestäms av
formel
 (5.5)
(5.5)
var
F
- värmebelastning på platsen, W:
(tG
— tO)
- temperaturskillnad på kylvätskan.
6.
Efter magnitud
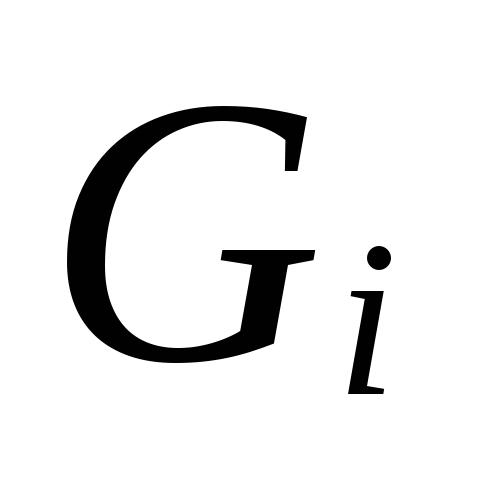
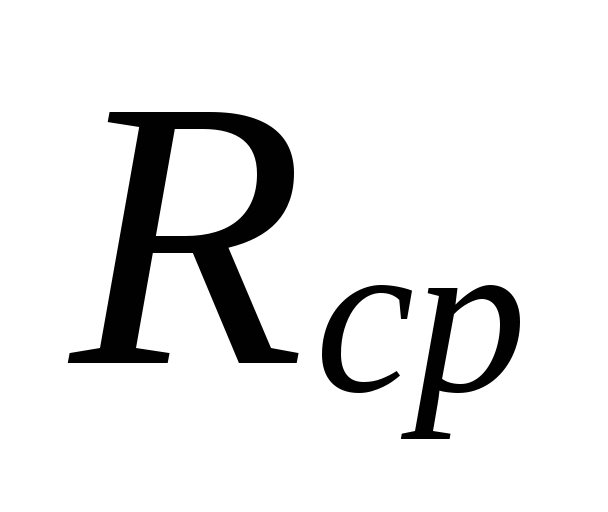
.

6.
För utvalda rörledningsdiametrar
och beräknad vattenförbrukning bestäms
kylvätskans hastighet v
och den faktiska specifika
friktionstrycksförlust Rf.
På
val av diametrar i områden med små
kylvätskeflöden kan vara
stora skillnader mellan
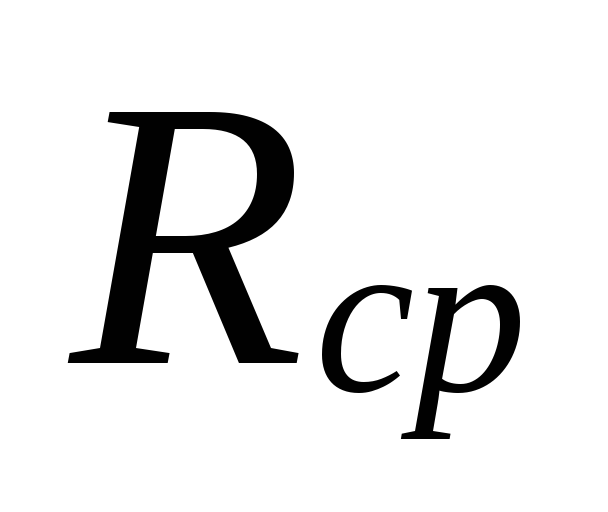
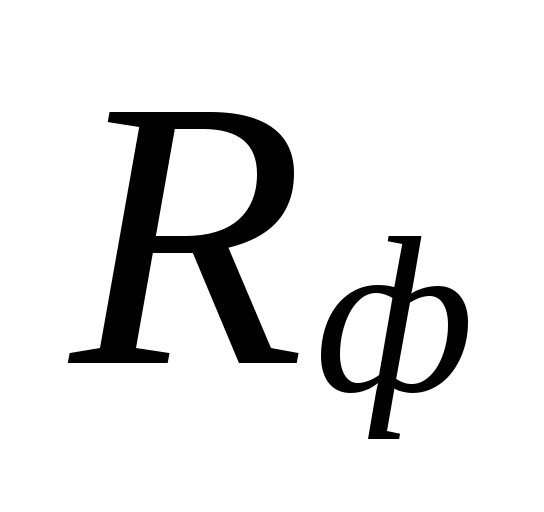
underskattade förluster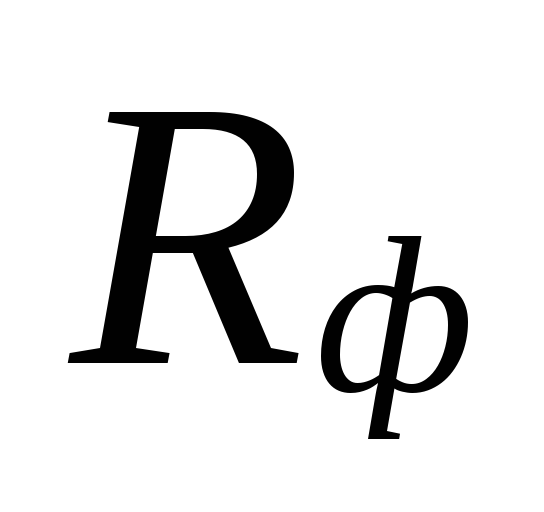
dessa områden kompenseras av en överskattning
kvantiteter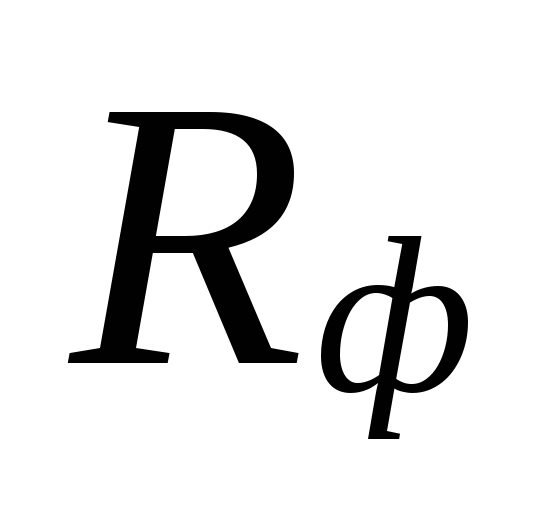
7.
Friktionstrycksförluster bestäms
på den beräknade arean, Pa:
 .
.
(5.6)
resultat
beräkningar förs in i tabell 5.2.
8.
Tryckförluster i lokal
motstånd med antingen formeln:
 ,
,
(5.7)
var
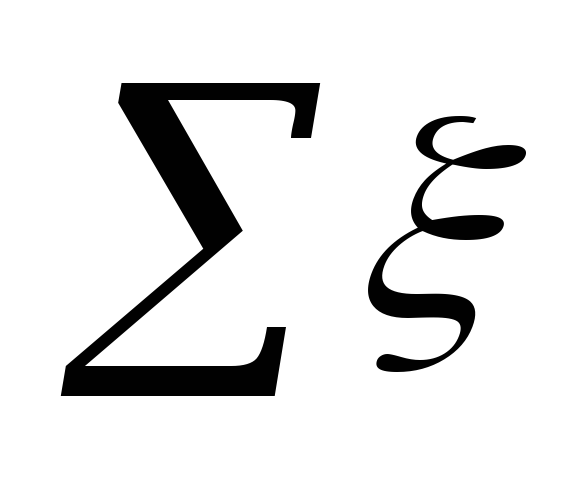
i bosättningsområdet.
Menande ξ
på varje plats sammanfattas i tabellen. 5.3.
Tabell 5.3 -
Lokala motståndskoefficienter
|
nr. p / p |
Namn |
Värderingar |
Anteckningar |
9.
Bestäm den totala tryckförlusten
inom varje område
 .
.
(5.8)
10. Definiera
total tryckförlust på grund av friktion och
i huvudsak i lokala motstånd
cirkulationsring
 .
.
(5.9)
11. Jämför Δp
Med ΔpR.
Total tryckförlust över ringen
måste vara mindre än ΔpR
på
 .
.
(5.10)
lager av engångsartiklar
tryck behövs på oredovisad in
beräkning av hydrauliskt motstånd.
Om förhållandena inte är det
utförs, är det nödvändigt på vissa
sektioner av ringen för att ändra diametern på rören.
12. Efter beräkning
huvudcirkulationsring
gör länkningen av de återstående ringarna. V
varje ny ring räknas endast
ytterligare icke-gemensamma områden,
kopplade parallellt med sektioner
huvudring.
Förlustdiskrepans
tryck på parallellkopplade
tomter tillåtna upp till 15 % med en återvändsgränd
rörelsen av vatten och upp till 5% - med förbigående.
tabell
5.2 - Resultat av hydraulisk beräkning
för värmesystem
|
På |
Förbi |
Förbi |
||||||||||||||
|
siffra |
Termisk |
Konsumtion |
Längd |
Diameter |
Fart |
Specifik |
Förluster |
Belopp |
Förluster |
d, |
v, |
R, |
Δptr, |
∑ξ |
Z, |
Rl+Z, |
Lektion 6
Förändring i gastemperatur längs gasledningens längd
I stationärt gasflöde, massan
flödeshastigheten i gasledningen är
 . (2.41)
. (2.41)
Faktum är att rörelsen av gas i gasledningen
är alltid icke-isotermisk. V
Under kompressionen värms gasen upp.
Även efter dess kylning vid COP, temperaturen
gas som kommer in i rörledningen
är cirka 2040С,
vilket är mycket högre än temperaturen
miljö (T).
I praktiken blir temperaturen på gasen
nära den omgivande temperaturen
endast för gasledningar med liten diameter
(Dy0.
Dessutom bör man ta hänsyn till det
rörledningsgas
är en riktig gas, som är inneboende
Joule-Thompson-effekten, som tar hänsyn till
absorption av värme under gasexpansion.
När temperaturen ändras längs längden
gasledningens gasrörelse beskrivs
ekvationssystem:
specifik energi ,
,
kontinuitet ,
,
stater ,
,
värmebalans .
.
Betrakta, i den första approximationen, ekvationen
värmebalans utan att ta hänsyn till effekten
Joule Thompson. Integrering av ekvationen
värmebalans
 ,
,
vi får
 , (2.42)
, (2.42)
var ;
;
KSR- genomsnitt på webbplatsen full
värmeöverföringskoefficient från gas till
miljö;
G är gasens massflödeshastighet;
cP–
genomsnittlig isobarisk värmekapacitet hos gasen.
ett värdetL kallas det dimensionslösa kriteriet
Shukhov
 (2.43)
(2.43)
Så gastemperaturen på slutet
gasledning kommer att vara
 . (2.44)
. (2.44)
På avstånd x från början
gasledningens gastemperatur bestäms
enligt formeln
 . (2.45)
. (2.45)
Förändring i temperatur längs gasledningens längd
är exponentiell (fig.
2.6).
Överväga
effekt av gastemperaturförändring på
pipelines prestanda.
Multiplicera båda sidor av den specifika ekvationen
energi på 2 och uttrycka ,
,
vi får
 . (2.46)
. (2.46)
Vi uttrycker gasens densitet på vänster sida
uttryck (2.46) från tillståndsekvationen
 ,
,
produktwfrån kontinuitetsekvationen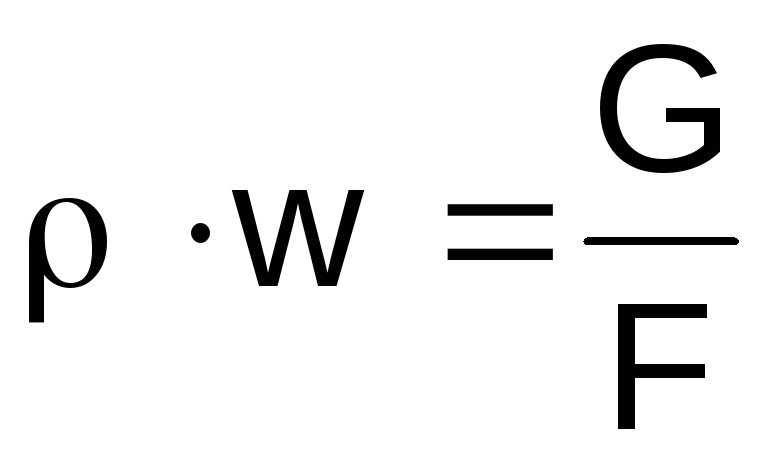
balans .
.
Med detta i åtanke, den specifika ekvationen
energi tar formen
 (2.47)
(2.47)
eller
 . (2.48)
. (2.48)
Betecknar
 och integrera den vänstra sidan av ekvationen
och integrera den vänstra sidan av ekvationen
(2.48) från PHdoPTILL, och till höger från THpunktTILL, vi får
 . (2.49)
. (2.49)
Genom att byta ut
 , (2.50)
, (2.50)
vi har
 . (2.51)
. (2.51)
Efter att ha integrerats i det angivna
gränser får vi

 . (2.52)
. (2.52)
Med hänsyn till (2,42)

eller
 , (2.53)
, (2.53)
var är en korrektionsfaktor som tar hänsyn till
är en korrektionsfaktor som tar hänsyn till
temperaturförändring längs gasledningens längd
(icke-isotermitet hos gasflödet).
Med hänsyn till (2.53), beroendet för att bestämma
massflödeshastighet av gas kommer att ta formen
 . (2.54)
. (2.54)
Värde Halltid större än en, alltså
gasens massflöde vid byte
temperatur längs gasledningens längd
(icke-isotermiskt flöde) alltid
mindre än i isotermiskt läge
(T=idem). Produkt THkallas medelintegralen
temperatur på gasen i rörledningen.
Med värdena för Shukhov-talet Shu4
gasflöde i rörledningen
överväg nästan isotermisk
vid T=idem. En sådan temperatur
läge är möjligt när man pumpar gas med
låga kostnader för gasledning
liten (mindre än 500 mm) diameter till en betydande
distans.
Effekt av ändrad gastemperatur
manifesterar sig för värdena för Shukhov-numret
Shu
På
gaspumpning närvaron av en gasspjäll
effekt leder till en djupare
gaskylning än bara med värmeväxling
med jord. I detta fall temperaturen
gas kan till och med falla under
temperatur T (Fig.
2.7).
Ris. 2.7. Inverkan av Joule-Thompson-effekten
på gastemperaturfördelningen över
rörledningens längd
1 - utan att ta hänsyn till Di; 2 - med
med hänsyn till Di
Sedan, med hänsyn till Joule-Thompson-koefficienten
lagen om temperaturförändring längs längden
tar formen
 , (2.55)
, (2.55)
5 Hydrauliska förluster
Skillnad
oljetryck i två sektioner av en
och samma pipeline, förutsatt att
den första är belägen uppströms, och
den andra - nedan, bestäms ekvation
Bernoulli
 ,
,
var
h2
– h1
- skillnaden i höjderna på tyngdpunkterna
avsnitt från en godtyckligt vald
horisontell nivå;
v1,
v2
– genomsnittliga hastigheter för olja i sektioner;
g - kraftacceleration
allvar;

hydrauliska förluster under rörelse
oljor från den första delen till den andra.
Ekvationen
Bernoulli i full användning
för beräkning av sugledningar för pumpar;
i andra fall första terminen,
vanligtvis försummat och övervägt:

hydraulisk
förluster brukar delas in i lokala
förluster och friktionsförluster längs längden
rörledningar (linjär).
1.5.1
lokala förluster
energier beror på lokala
hydrauliskt motstånd,
orsakar flödesförvrängning. Lokal
motstånd är: sammandragningar,
expansion, avrundning av rörledningar,
filter, styrutrustning och
reglering etc. Vid strömning
vätskor genom lokala motstånd
dess hastighet ändras och det är det vanligtvis
stora virvlar.
Förluster
tryck från lokala motstånd
bestäms av formeln Weisbach:
 MPa
MPa
(eller
 Pa),
Pa),
var

förlust,
v
är medelflödeshastigheten över tvärsnittet
i ett rör bakom lokalt motstånd, m/s;
,
N/m3;
g=9,81 m/s2.
Varje
lokalt motstånd karakteriseras
genom dess koefficientvärde

Med turbulent flöde, värdena
motstånd och mycket lite förändring
med en förändring av sektionens storlek, hastighet
vätskeflöde och viskositet. Så
anta att de inte beror på antalet
Reynolds Re.
Värderingar

till exempel för tees med samma
kanaldiametrar tas lika,
om:
strömmar
lägga ihop, divergera; flöde
godkänd;









på
rörböjning

Värderingar

i hydrauliska system av utrustning, hämtade från
referenslitteratur.
På
laminärt flöde (Re
Förluster
tryck från lokala motstånd kl
laminärt flöde bestäms av
formel:
 MPa
MPa
var

= a

Kvantiteter
tryckförlust i standard
hydrauliska anordningar för
nominellt flöde vanligtvis
anges i deras tekniska specifikationer.
1.5.2
Förlust på
längdfriktion
är den energiförlust som uppstår
i raka rör med konstant tvärsnitt,
de där. med jämnt vätskeflöde,
och öka i proportion till längden
rör. Dessa förluster beror på interna
friktion i en vätska, och har därför
placeras i både grova och släta rör.
Förluster
rörlednings friktionstryck
bestäms av formeln Darcy:
 MPa
MPa
var

l
och d
- rörledningens längd och inre diameter,
mm.
Detta
formeln är tillämplig både för laminär,
såväl som i turbulent flöde; skillnad
består endast av koefficientens värden

På
laminärt flöde (Re
På
friktionskoefficient för turbulent flöde
är inte bara en funktion av Re, utan
beror också på grovheten hos den inre
rörytan. För hydrauliskt
slät rör,
de där. med en grovhet som
praktiskt taget inte påverkar dess motstånd,
turbulent friktionskoefficient
läge kan bestämmas av formeln PC.
Konakova:

rör
anses hydrauliskt smidigt om
(d/k)>(Re/20),
där k är ekvivalent grovhet,
mm. Till exempel för nytt sömlöst stål
rör k≈0,03
mm, och efter flera års drift
k≈0,2
mm, för nya sömlösa rör av
icke-järnmetaller k≈0,005
mm. Dessa rör används ofta i
hydrauliska system av verktygsmaskiner.
Koefficient
friktion i den turbulenta regimen kan vara
bestämma med formeln Altshulya,
vara universell (dvs tillämplig
hur som helst):

2. Flödesegenskaper för rörledningsflödesmodulen
Låt oss komma ihåg
linjär förlustformel - Darcy-formel
- Weisbach:
 .
.
uttrycka
i denna formel, hastigheten V
genom flöde Q
från förhållandet
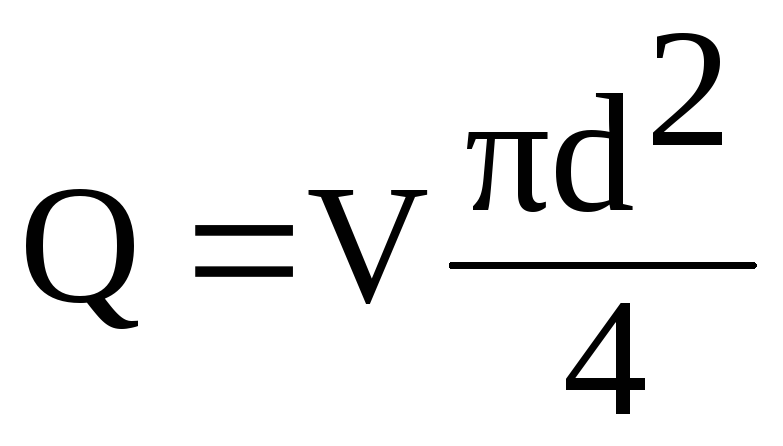
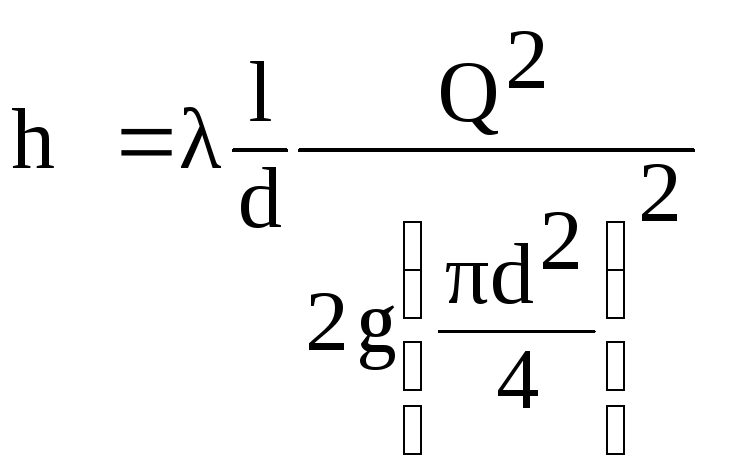
(6.1)
För
rörledning med en viss diameter
komplex av mängder
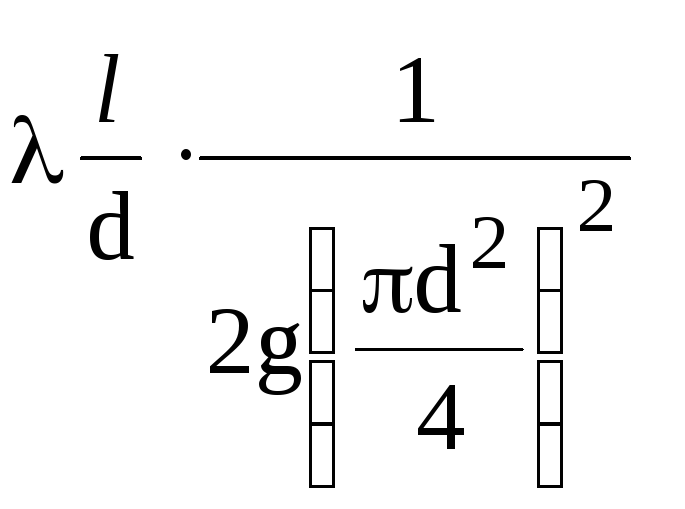
konstant (1/K2),
förutom den hydrauliska koefficienten
friktion λ. Baserat på konceptet
genomsnittlig ekonomisk hastighet Vt.ex
låt oss visa att den angivna koefficienten λ
kan hänföras till detta komplex, eftersom v
I det här fallet kommer Reynolds-numret att vara
har en specifik betydelse:
 ,
,
och på Nikuradze-diagrammet, koefficienten λ in
detta fall kommer att ha en specifik
menande.
Rättfärdiga
legitimiteten att införa konceptet
genomsnittlig ekonomisk hastighet enligt följande
resonemang.
hydraulisk
system, såsom VVS,
du kan hoppa över en viss utgift
gjorda av rör med olika diametrar. På
Samtidigt, med en ökning av diametern d,
därför en minskning av hastigheten V
kapitalutgifterna kommer att stiga, och
driftskostnaderna kommer
minskning på grund av en minskning av hydrauliken
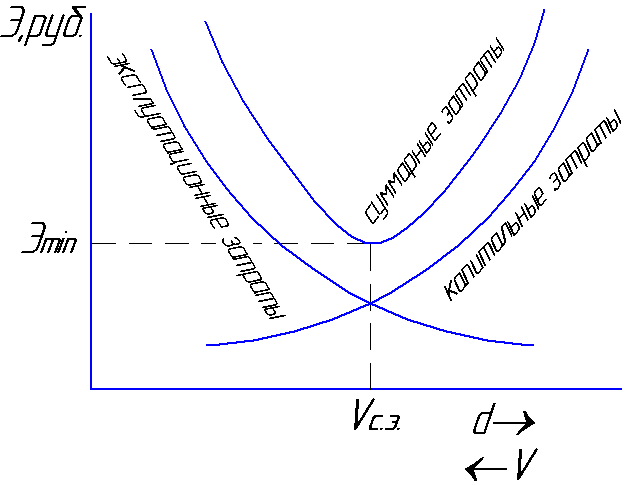
förluster. Den hastighet med vilken totalen
kostnaderna blir minimala
kommer att kallas den genomsnittliga ekonomiska
hastighet Vt.ex
= 0,8 ... 1,3 m/s (Fig. 6.1).
fig.6.1
Sedan
den linjära förlustformeln (6.1) tar formen
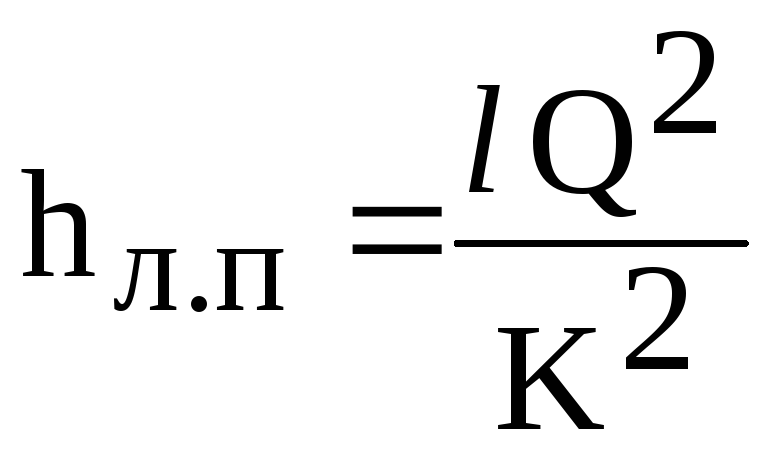
(6.2)
var
K - flödeskarakteristik för rörledningen
(flödesmodul), beroende på material
rörledning, diameter och flöde. är tagen
från borden.
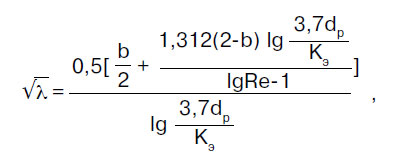
 ),C
),C ,
,