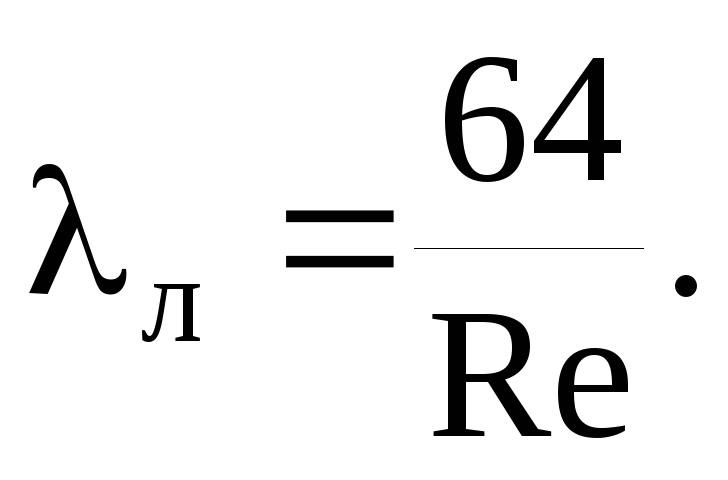1. แรงดันอุทกสถิต
ความดันอุทกสถิตคือ
แรงอัดภายในเนื่องจาก
โดยการกระทำของแรงภายนอกที่ใช้กับ
จุดที่กำหนดในของเหลว ความกดดันดังกล่าว
ในทุกทิศทุกทางก็เหมือนกันและขึ้นอยู่
บนตำแหน่งของจุดในของเหลวที่อยู่นิ่ง
มิติของแรงดันอุทกสถิต
ในระบบ MKGSS - kg / cm2 หรือ t / m2
ในระบบ SI - N/m2
อัตราส่วนหน่วยพื้นฐาน
ความดัน:
|
กก./ซม.2 |
N/m2 |
|
|
บรรยากาศทางเทคนิค |
1 |
98066,5 |
|
มิลลิเมตรน้ำคอลัมน์ |
0,0001 |
9,80665 |
|
มิลลิเมตรปรอท |
0,00136 |
133,32 |
ในการคำนวณเชิงปฏิบัติ 1 เทคนิค
บรรยากาศ \u003d 1 กก. / ซม. 2 \u003d น้ำ 10 เมตร ศิลปะ. =
735 mmHg ศิลปะ. = 98070 นิวตัน/ตารางเมตร
สำหรับของเหลวที่ไม่สามารถบีบอัดได้นั่นคือ
สมดุลภายใต้กำลัง
แรงโน้มถ่วงเต็มไฮโดรสแตติก
แรงดันจุด:
p=p+

โดยที่ p คือแรงกดดันต่อค่าว่าง
พื้นผิวของเหลว

สูง h กับพื้นที่
ภาพตัดขวางเท่ากับหนึ่ง;
h - ความลึกของการแช่
คะแนน;

สำหรับของเหลวบางชนิด ค่า
ความถ่วงจำเพาะที่ใช้ในการแก้
งานจะได้รับในภาคผนวก (แท็บ
P-3).
ค่าของแรงดันเกิน
บรรยากาศ (pเอ)
เรียกว่า manometric หรือ
แรงดันเกิน:

ถ้าแรงกดบนพื้นผิวที่ว่าง
เท่ากับบรรยากาศ แล้วเกิน
ความดัน pม=

ความกดอากาศต่ำ
ปริมาณเรียกว่าสูญญากาศ:
Rwack= pเอ- ร.
วิธีแก้ปัญหาส่วนใหญ่ของเรื่องนี้
ส่วนที่เกี่ยวข้องกับการใช้
สมการพื้นฐานของไฮโดรสแตติก

โดยที่ z คือพิกัดหรือ
เครื่องหมายจุด
1. ข้อมูลทั่วไปเกี่ยวกับการคำนวณไฮดรอลิกของท่อ
เมื่อคำนวณ
กำลังพิจารณาท่อ
แรงกดสม่ำเสมอ
การเคลื่อนที่ของของเหลวใดๆ
ระบอบเผด็จการในรูปทรงกระบอกกลม
ท่อ. ของเหลวในท่อแรงดัน
อยู่ภายใต้ความกดดันและ
ส่วนตัดขวางของพวกเขาสมบูรณ์
เติมเต็ม การเคลื่อนที่ของของไหลตามทาง
ไปป์ไลน์เกิดขึ้นเป็นผล
ความจริงที่ว่าแรงกดดันที่จุดเริ่มต้นนั้นมากกว่า
ในที่สุด.
ไฮดรอลิค
การคำนวณทำขึ้นเพื่อกำหนด
เส้นผ่าศูนย์กลางท่อ d
กับที่รู้จัก
ความยาวเพื่อให้แน่ใจว่าข้าม
อัตราการไหลที่แน่นอน คิว
หรือก่อตั้ง
ที่เส้นผ่านศูนย์กลางและความยาวที่กำหนด
ความดันและการไหลของของเหลว ท่อส่ง
ขึ้นอยู่กับความยาวและรูปแบบของพวกเขา
สถานที่แบ่งออกเป็นแบบง่าย
และซับซ้อน สู่ท่อธรรมดา
รวมถึงท่อที่ไม่มี
แตกกิ่งก้านตามยาวด้วยค่าคงที่
ค่าใช้จ่ายเดียวกัน
ท่อส่ง
ประกอบด้วยท่อที่มีเส้นผ่านศูนย์กลางเท่ากัน
ตามความยาวทั้งหมดหรือจากส่วนของท่อที่แตกต่างกัน
เส้นผ่านศูนย์กลางและความยาว คดีสุดท้าย
หมายถึงการเชื่อมต่อแบบอนุกรม
ท่อธรรมดา
ขึ้นอยู่กับความยาวด้วยพล็อตของท้องถิ่น
แนวต้านแบ่งออกเป็นระยะสั้นและ
ยาว. สั้น
ท่อ
เป็น
ท่อที่มีความยาวสั้นเพียงพอ
ซึ่งการต่อต้านในท้องถิ่น
ทำขึ้นมากกว่า 10% ของไฮดรอลิค
การสูญเสียความยาว ตัวอย่างเช่น พวกเขารวมถึง:
ท่อดูด ดูด
ท่อของปั๊มใบพัด กาลักน้ำ (ความดัน
ท่อน้ำใต้ตลิ่งถนน)
ท่อภายในอาคารและโครงสร้าง
ฯลฯ
ยาว
ท่อ
เรียกว่า
ท่อมีขนาดค่อนข้างใหญ่
ความยาวที่ศีรษะสูญเสียไปตามความยาว
มีจำนวนมากกว่าท้องถิ่นอย่างมาก
ความสูญเสีย การสูญเสียในท้องถิ่นคือ
น้อยกว่า 5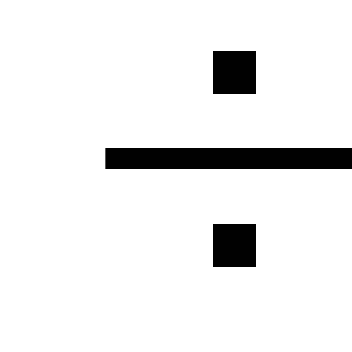
การสูญเสียตามความยาวของท่อและดังนั้น
สามารถละเลยหรือแนะนำได้ที่
การคำนวณไฮดรอลิกเพิ่มขึ้น
ค่าสัมประสิทธิ์เท่ากับ 1.05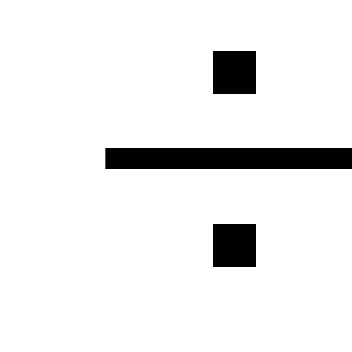
ท่อยาวเข้าสู่ระบบ
เครือข่ายน้ำประปาท่อสูบน้ำ
สถานี ท่อร้อยสาย และท่อส่ง
ผู้ประกอบการอุตสาหกรรมและ
วัตถุประสงค์ทางการเกษตรและ
ฯลฯ
ท่อที่ซับซ้อน
มีกิ่งก้านแตกต่างกันตามยาว
เหล่านั้น. ไปป์ไลน์ประกอบด้วยโครงข่ายท่อ
เส้นผ่านศูนย์กลางและความยาวที่แน่นอน ซับซ้อน
ท่อแบ่งออกเป็น
ขนาน, ทางตัน (แตกแขนง),
ท่อวงแหวน (ปิด)
รวมอยู่ในเครือข่ายน้ำประปา
ไฮดรอลิค
การคำนวณไปป์ไลน์ลดลงเป็น
มักจะแก้ปัญหาหลักสามประการ:
-
คำนิยาม
การไหลของท่อ คิว,
ถ้ารู้จัก
ความดัน ชม,
ระยะเวลา l
และเส้นผ่านศูนย์กลาง d
ท่อส่ง,
เนื่องจากความพร้อมใช้งานของท้องถิ่นบางอย่าง
การต่อต้านหรือขาดหายไป -
คำนิยาม
ความดันที่ต้องการ ชม,
จำเป็นในการรักษาความปลอดภัยผ่าน
รู้จักกระแส คิว
โดยท่อ
ระยะเวลา l
และเส้นผ่านศูนย์กลาง d; -
คำนิยาม
เส้นผ่าศูนย์กลางท่อ d
เมื่อไร
ค่าหัวที่รู้จัก ชม,
ค่าใช้จ่าย คิว
และความยาว l.
อัตราการไหลของของเหลวคือ
โดยที่ q > การออกแบบการไหลของของไหล m3/s;
- พื้นที่ส่วนสดของท่อ m2
ค่าสัมประสิทธิ์ความต้านทานแรงเสียดทาน λ ถูกกำหนดตามกฎของชุดของกฎ SP 40-102-2000 "การออกแบบและติดตั้งท่อสำหรับระบบน้ำประปาและระบบระบายน้ำทิ้งที่ทำจากวัสดุโพลีเมอร์ ข้อกำหนดทั่วไป":
โดยที่ b คือจำนวนความคล้ายคลึงกันของระบอบการไหลของของไหล สำหรับ b > 2 จะใช้ b = 2
โดยที่ Re คือหมายเลข Reynolds จริง
โดยที่ ν คือสัมประสิทธิ์ความหนืดจลนศาสตร์ของของเหลว m²/s เมื่อคำนวณท่อน้ำเย็นจะเท่ากับ 1.31 10-6 m² / s - ความหนืดของน้ำที่อุณหภูมิ +10 ° C;
Rekv > - หมายเลข Reynolds ที่สอดคล้องกับจุดเริ่มต้นของขอบเขตกำลังสองของความต้านทานไฮดรอลิก
โดยที่ Ke คือความขรุขระของไฮดรอลิกของวัสดุท่อ m สำหรับท่อที่ทำจากวัสดุโพลีเมอร์ Ke = 0.00002 m จะถูกนำมาหากผู้ผลิตท่อไม่ให้ค่าความหยาบอื่นๆ
ในกรณีของการไหลเมื่อ Re ≥ Rekv ค่าที่คำนวณได้ของพารามิเตอร์ b จะเท่ากับ 2 และสูตร (4) จะลดความซับซ้อนลงอย่างมาก โดยเปลี่ยนเป็นสูตร Prandtl ที่รู้จักกันดี:
ที่ Ke = 0.00002 m พื้นที่ความต้านทานกำลังสองเกิดขึ้นที่อัตราการไหลของน้ำ (ν = 1.31 10-6 m²/s) เท่ากับ 32.75 m/s ซึ่งในทางปฏิบัติไม่สามารถบรรลุได้ในระบบประปาสาธารณะ
สำหรับการคำนวณทุกวันแนะนำให้ใช้ nomograms และสำหรับการคำนวณที่แม่นยำยิ่งขึ้น - "ตารางสำหรับการคำนวณไฮดรอลิกของท่อที่ทำจากวัสดุโพลีเมอร์" เล่มที่ 1 "ท่อแรงดัน" (A.Ya. Dobromyslov, M. , VNIIMP, 2004)
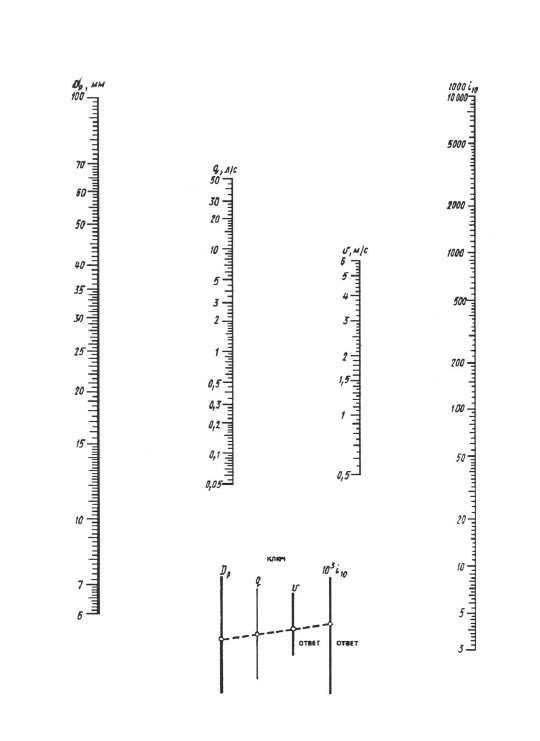
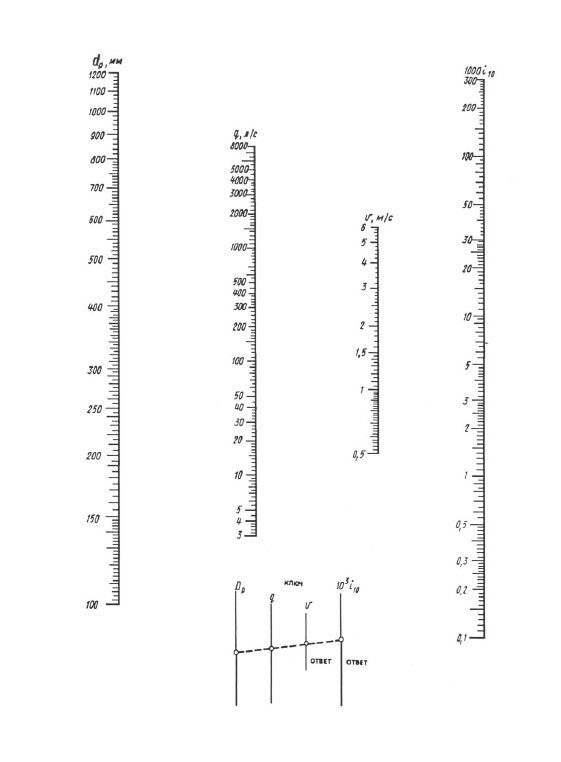
เมื่อคำนวณตาม nomograms ผลลัพธ์จะทำได้โดยการซ้อนทับของไม้บรรทัด - คุณควรเชื่อมต่อจุดกับค่าของเส้นผ่านศูนย์กลางที่คำนวณบนสเกล dp กับจุดที่มีค่าของอัตราการไหลที่คำนวณได้ใน q (l / s) มาตราส่วนด้วยเส้นตรง ต่อด้วยเส้นตรงนี้จนกว่าจะตัดกับมาตราส่วนความเร็ว V และค่าความสูญเสียจำเพาะ 1000 i (mm/m) จุดตัดของเส้นตรงที่มีมาตราส่วนเหล่านี้ให้ค่า V และ 1,000 i
ดังที่คุณทราบ ค่าไฟฟ้าสำหรับสูบของเหลวเป็นสัดส่วนโดยตรงกับค่าของ H (ceteris paribus) การแทนที่นิพจน์ ( 3 ) ลงในสูตร ( 2 ) จะเห็นได้ง่ายว่าค่าของ i (และด้วยเหตุนี้ H) เป็นสัดส่วนผกผันกับเส้นผ่านศูนย์กลางที่คำนวณได้ dp ถึงระดับที่ห้า
ดังที่แสดงไว้ข้างต้นว่าค่า dp นั้นขึ้นอยู่กับความหนาของผนังท่อ e: ยิ่งผนังยิ่งบาง dp สูงขึ้น และดังนั้น การสูญเสียแรงดันที่ลดลงอันเนื่องมาจากแรงเสียดทานและค่าไฟฟ้าก็จะยิ่งลดลง
หากค่า MRS ของท่อเปลี่ยนแปลงด้วยเหตุผลใดก็ตาม จะต้องคำนวณเส้นผ่านศูนย์กลางและความหนาของผนัง (SDR) ใหม่
โปรดทราบว่าในหลายกรณี การใช้ท่อที่มี MRS 10 แทนท่อที่มี MRS 8 โดยเฉพาะท่อที่มี MRS 6.3 ทำให้สามารถลดขนาดเส้นผ่านศูนย์กลางของท่อได้หนึ่งขนาด ดังนั้นในยุคของเราการใช้โพลิเอทิลีน PE 80 (MRS 8) และ PE 100 (MRS 10) แทนโพลิเอทิลีน PE 63 (MRS 6.3) ในการผลิตท่อจึงไม่เพียงช่วยลดความหนาของผนังท่อเท่านั้น แต่ยังลดน้ำหนักอีกด้วย และการใช้วัสดุ แต่ยังลดต้นทุนด้านพลังงานสำหรับการสูบของเหลว (ceteris paribus)
ในช่วงไม่กี่ปีที่ผ่านมา (หลังปี 2556) ท่อที่ทำจากโพลีเอทิลีน PE80 ถูกแทนที่เกือบทั้งหมดจากการผลิตด้วยท่อที่ทำจากโพลีเอทิลีนเกรด PE100 อธิบายได้จากข้อเท็จจริงที่ว่าวัตถุดิบที่ใช้ทำท่อส่งมาจากต่างประเทศด้วยยี่ห้อ PE100และความจริงที่ว่าเกรดโพลีเอทิลีน 100 มีลักษณะความแข็งแรงมากกว่าเนื่องจากผลิตท่อที่มีลักษณะเช่นเดียวกับท่อที่ทำจาก PE80 แต่มีผนังทินเนอร์จึงเพิ่มปริมาณงานของท่อโพลีเอทิลีน
Nomogram สำหรับกำหนดการสูญเสียแรงดันในท่อที่มีขนาดเส้นผ่าศูนย์กลาง 6, 100 มม.
Nomogram สำหรับกำหนดการสูญเสียแรงดันในท่อที่มีขนาดเส้นผ่าศูนย์กลาง 100, 1200 มม.
เกณฑ์ Reynolds
การพึ่งพาอาศัยกันนี้เกิดขึ้นโดยนักฟิสิกส์และวิศวกรชาวอังกฤษ Osborne Reynolds (1842-1912)
เกณฑ์ที่ช่วยตอบคำถามว่ามีความจำเป็นต้องพิจารณาความหนืดหรือไม่คือ Reynolds number Re มันเท่ากับอัตราส่วนของพลังงานของการเคลื่อนที่ขององค์ประกอบของของไหลที่ไหลต่อการทำงานของแรงเสียดทานภายใน
พิจารณาองค์ประกอบของเหลวลูกบาศก์ที่มีความยาวขอบ n พลังงานจลน์ของธาตุคือ:
ตามกฎของนิวตัน แรงเสียดทานที่กระทำต่อธาตุของไหลถูกกำหนดดังนี้:
การทำงานของแรงนี้เมื่อเคลื่อนที่องค์ประกอบของเหลวไปเป็นระยะทาง n is
และอัตราส่วนของพลังงานจลน์ของธาตุของไหลต่อการทำงานของแรงเสียดทานคือ
เราลดและรับ:
Re เรียกว่าหมายเลข Reynolds
ดังนั้น Re เป็นปริมาณไร้มิติที่กำหนดบทบาทสัมพัทธ์ของแรงหนืด
ตัวอย่างเช่น หากขนาดของร่างกายที่ของเหลวหรือก๊าซสัมผัสกันมีขนาดเล็กมาก แม้ว่าจะมีความหนืดต่ำ Re จะไม่มีนัยสำคัญและแรงเสียดทานจะมีบทบาทสำคัญ ในทางตรงกันข้าม หากขนาดของตัวเครื่องและความเร็วมีขนาดใหญ่ ดังนั้น Re >> 1 และแม้แต่ความหนืดที่มากก็แทบไม่มีผลกระทบต่อธรรมชาติของการเคลื่อนที่เลย
อย่างไรก็ตาม จำนวน Reynolds ที่ไม่ใหญ่เสมอไปหมายความว่าความหนืดไม่ได้มีบทบาทใดๆ ดังนั้นเมื่อถึงค่าจำนวน Re ที่มีขนาดใหญ่มาก (หลายหมื่นหรือหลายแสน) แผ่นเรียบ (จากลามินาลามินา - "จาน") จะกลายเป็นกระแสปั่นป่วน (จากภาษาละติน turbulentus - "พายุ" , "วุ่นวาย") พร้อมกับของเหลวที่เคลื่อนไหวไม่มั่นคง เอฟเฟกต์นี้สามารถสังเกตได้หากคุณค่อยๆ เปิดก๊อกน้ำ: กระแสน้ำบาง ๆ มักจะไหลอย่างราบรื่น แต่ด้วยความเร็วของน้ำที่เพิ่มขึ้น ความราบรื่นของการไหลจะถูกรบกวน ในเครื่องบินไอพ่นที่ไหลออกมาภายใต้ความกดอากาศสูง อนุภาคของเหลวจะเคลื่อนที่แบบสุ่ม สั่น การเคลื่อนไหวทั้งหมดมาพร้อมกับส่วนผสมที่เข้มข้น
การปรากฏตัวของความปั่นป่วนเพิ่มการลากอย่างมาก ในท่อส่ง ความเร็วการไหลแบบปั่นป่วนจะน้อยกว่าความเร็วการไหลแบบราบเรียบที่ความดันลดลงเท่ากัน แต่ความวุ่นวายก็ไม่ได้เลวร้ายเสมอไป เนื่องจากการผสมระหว่างความปั่นป่วนมีความสำคัญมาก การถ่ายเทความร้อน - การทำความเย็นหรือความร้อนของมวลรวม - เกิดขึ้นอย่างเข้มข้นมากขึ้น การแพร่กระจายของปฏิกิริยาเคมีจะเร็วขึ้น
สมการการเคลื่อนที่อยู่กับที่ของเบอร์นูลลี
หนึ่งในสมการที่สำคัญที่สุดของไฮโดรแมคคานิกส์ได้รับในปี ค.ศ. 1738 โดยนักวิทยาศาสตร์ชาวสวิส แดเนียล เบอร์นูลลี (ค.ศ. 1700-1782) ครั้งแรกที่เขาอธิบายการเคลื่อนที่ของของไหลในอุดมคติได้ แสดงไว้ในสูตรเบอร์นูลลี
ของไหลในอุดมคติคือของไหลที่ไม่มีแรงเสียดทานระหว่างองค์ประกอบของของไหลในอุดมคติ เช่นเดียวกับระหว่างของไหลในอุดมคติกับผนังของภาชนะ
สมการการเคลื่อนที่อยู่กับที่ที่มีชื่อของเขาคือ:
โดยที่ P คือความดันของของเหลว ρ คือความหนาแน่น v คือความเร็วของการเคลื่อนที่ g คือความเร่งของการตกอย่างอิสระ h คือความสูงที่องค์ประกอบของของเหลวตั้งอยู่
ความหมายของสมการเบอร์นูลลีคือภายในระบบที่เต็มไปด้วยของเหลว (ส่วนท่อ) พลังงานทั้งหมดของแต่ละจุดจะไม่เปลี่ยนแปลงเสมอ
สมการเบอร์นูลลีมีสามเทอม:
- ρ⋅v2/2 - แรงดันไดนามิก - พลังงานจลน์ต่อหน่วยปริมาตรของน้ำมันขับ
- ρ⋅g⋅h - แรงดันน้ำหนัก - พลังงานศักย์ต่อหน่วยปริมาตรของของเหลว
- P - แรงดันสถิตในต้นกำเนิดคืองานของแรงดันและไม่ได้เป็นตัวแทนของพลังงานสำรองชนิดพิเศษใด ๆ ("พลังงานแรงดัน")
สมการนี้อธิบายว่าทำไมในส่วนที่แคบของท่อความเร็วของการไหลจึงเพิ่มขึ้นและความดันบนผนังท่อจะลดลง ความดันสูงสุดในท่อถูกตั้งค่าไว้อย่างแม่นยำในตำแหน่งที่ท่อมีหน้าตัดที่ใหญ่ที่สุด ส่วนที่แคบของท่อมีความปลอดภัยในเรื่องนี้ แต่ความดันในนั้นสามารถลดลงได้มากจนของเหลวเดือด ซึ่งอาจนำไปสู่การเกิดโพรงอากาศและการทำลายวัสดุท่อ
สมการเนเวียร์-สโตกส์สำหรับของเหลวหนืด
ในสูตรที่เข้มงวดยิ่งขึ้น การพึ่งพาเชิงเส้นของแรงเสียดทานหนืดต่อการเปลี่ยนแปลงความเร็วของของไหลเรียกว่าสมการเนเวียร์-สโตกส์ โดยคำนึงถึงการอัดตัวของของเหลวและก๊าซ และต่างจากกฎของนิวตัน ไม่เพียงแต่จะใช้ได้กับพื้นผิวของวัตถุที่เป็นของแข็งเท่านั้น แต่ยังใช้ได้ทุกจุดในของเหลวด้วย (ใกล้พื้นผิวของวัตถุที่เป็นของแข็งในกรณีที่ไม่สามารถบีบอัดได้ ของเหลว สมการเนเวียร์-สโตกส์ และกฎของนิวตันตรงกัน)
ก๊าซใดๆ ที่ตรงตามเงื่อนไขของตัวกลางแบบต่อเนื่องจะเป็นไปตามสมการของเนเวียร์-สโตกส์ด้วย เช่น คือของไหลของนิวตัน
ความหนืดของของเหลวและก๊าซมักจะมีนัยสำคัญที่ความเร็วค่อนข้างต่ำ ดังนั้นบางครั้งจึงกล่าวกันว่าอุทกพลศาสตร์ของออยเลอร์เป็นกรณีพิเศษ (จำกัด) ของอุทกพลศาสตร์ Navier-Stokes ความเร็วสูง
ที่ความเร็วต่ำตามกฎความฝืดหนืดของนิวตัน แรงลากของร่างกายจะเป็นสัดส่วนกับความเร็ว ที่ความเร็วสูง เมื่อความหนืดหยุดมีบทบาทสำคัญ ความต้านทานของร่างกายจะเป็นสัดส่วนกับกำลังสองของความเร็ว (ซึ่งถูกค้นพบครั้งแรกและพิสูจน์โดยนิวตัน)
ลำดับการคำนวณไฮดรอลิก
1.
เลือกการไหลเวียนหลัก
ระบบทำความร้อนแบบวงแหวน (ส่วนใหญ่
อยู่ในตำแหน่งที่เสียเปรียบในไฮดรอลิก
สัมพันธ์) ในปลายท่อสองทางตัน
ระบบคือวงแหวนที่ลอดผ่าน
เครื่องมือที่ต่ำกว่าของระยะไกลที่สุดและ
ไรเซอร์โหลดในท่อเดียว -
ผ่านระยะไกลและโหลดมากที่สุด
ไรเซอร์
ตัวอย่างเช่น
ในระบบทำความร้อนแบบสองท่อด้วย
การเดินสายบน การไหลเวียนหลัก
แหวนจะผ่านจากจุดความร้อน
ผ่านไรเซอร์หลัก, สายอุปทาน,
ผ่านไรเซอร์ที่ห่างไกลที่สุด ให้ความร้อน
เครื่องใช้ไฟฟ้าชั้นล่าง สายกลับ
ถึงจุดให้ความร้อน
วี
ระบบที่มีการเคลื่อนที่ของน้ำที่เกี่ยวข้องใน
แหวนถูกนำมาเป็นแหวนหลัก
ผ่านตรงกลางมากที่สุด
ยืนโหลด
2.
วงแหวนหมุนเวียนหลักแตก
เป็นแปลง (เนื้อเรื่องมีลักษณะ
การไหลของน้ำคงที่และเหมือนกัน
เส้นผ่านศูนย์กลาง) แผนภาพแสดง
หมายเลขส่วน ความยาวและความร้อน
โหลด ภาระความร้อนของ main
แปลงถูกกำหนดโดยการสรุป
ภาระความร้อนที่ให้บริการโดยสิ่งเหล่านี้
แปลง เพื่อเลือกเส้นผ่านศูนย์กลางท่อ
ใช้สองปริมาณ:
ก)
ให้น้ำไหล;
ข)
การสูญเสียแรงดันจำเพาะโดยประมาณ
สำหรับแรงเสียดทานในการออกแบบหมุนเวียน
แหวน Rพุธ.
สำหรับ
การคำนวณ Rcp
ต้องรู้ความยาวของสายหลัก
แหวนหมุนเวียนและการคำนวณ
ความดันหมุนเวียน
3.
การไหลเวียนที่คำนวณได้
สูตรความดัน
 ,
,
(5.1)
ที่ไหน
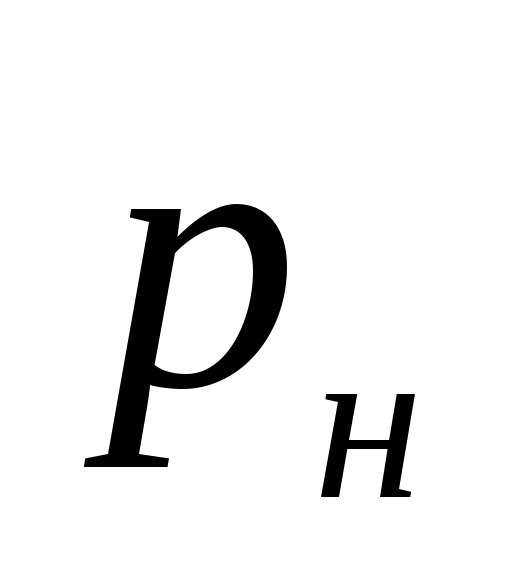
แรงดันที่เกิดจากปั๊ม Pa.
แนวทางปฏิบัติในการออกแบบระบบ
ความร้อนแสดงให้เห็นว่ามากที่สุด
ขอแนะนำให้ใช้แรงดันของปั๊ม
เท่ากัน
 ,
,
(5.2)
ที่ไหน
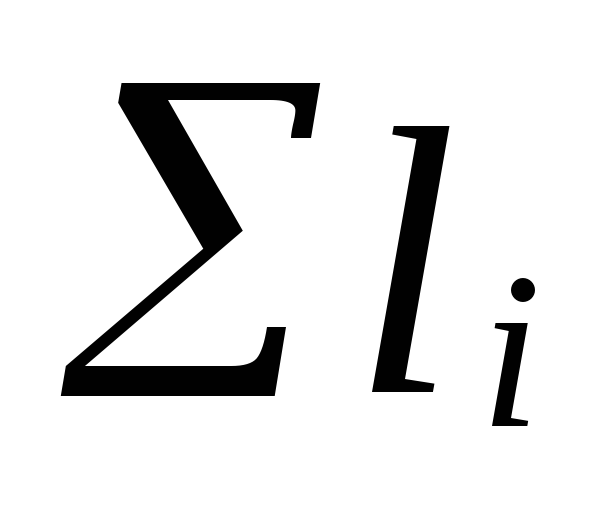
ผลรวมของความยาวของส่วนของการไหลเวียนหลัก
แหวน;
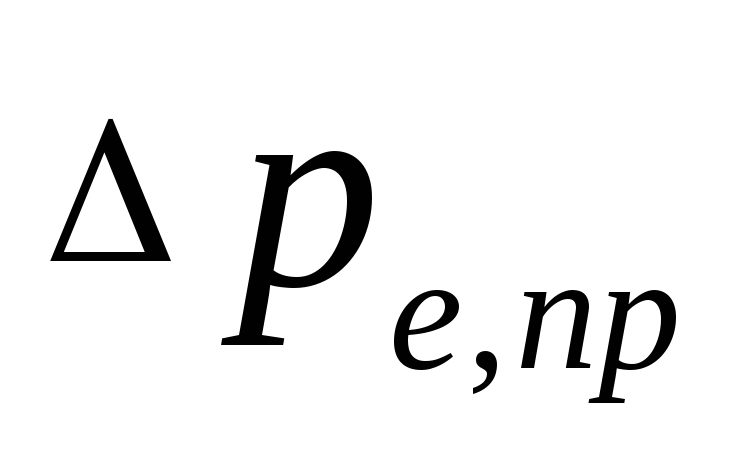
ความดันธรรมชาติที่เกิดขึ้นเมื่อ
ระบายความร้อนด้วยน้ำในเครื่องใช้ไฟฟ้า, ปะ, เป็นไปได้
กำหนดวิธีการ
 ,
,
(5.3)
ที่ไหน
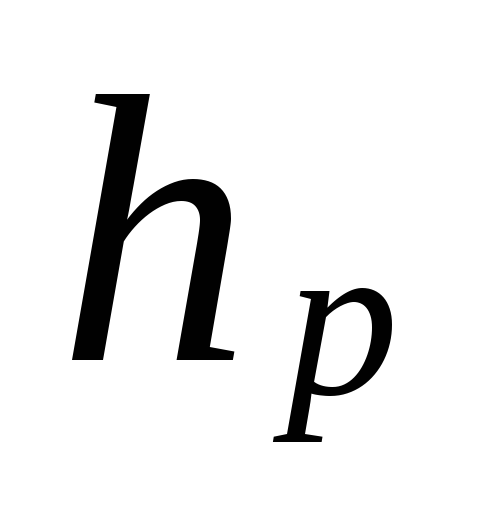
ระยะห่างจากจุดศูนย์กลางปั๊ม (ลิฟต์)
ถึงศูนย์กลางของอุปกรณ์ชั้นล่าง ม.
ความหมาย
ค่าสัมประสิทธิ์ เป็นไปได้
พิจารณาจากตารางที่ 5.1
ตาราง
5.1 - ความหมาย c
ขึ้นอยู่กับอุณหภูมิการออกแบบ
น้ำในระบบทำความร้อน
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
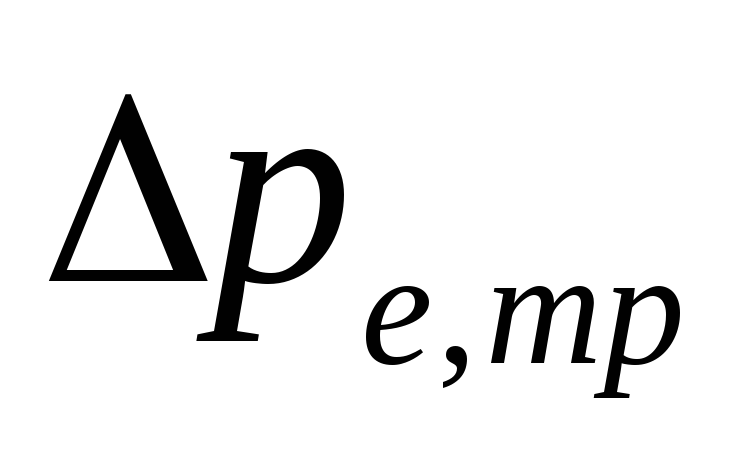
ความดันธรรมชาติใน
อันเป็นผลมาจากการระบายความร้อนด้วยน้ำในท่อ
.
วี
ระบบสูบน้ำพร้อมสายไฟด้านล่าง
ขนาด
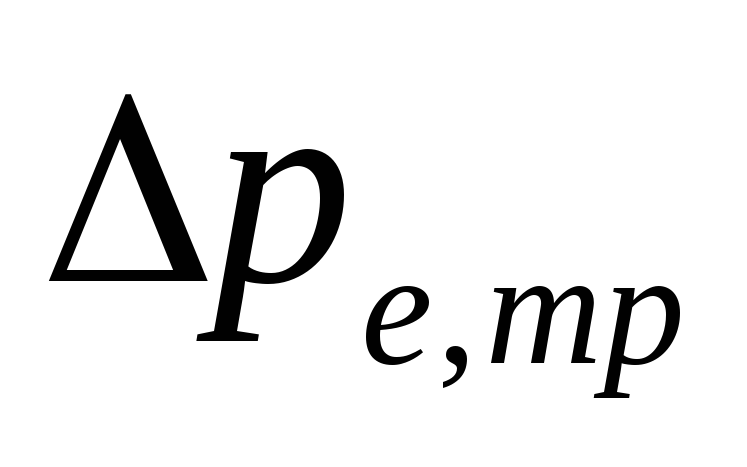
-
ถูกกำหนดแล้ว
การสูญเสียความดันแรงเสียดทานจำเพาะ
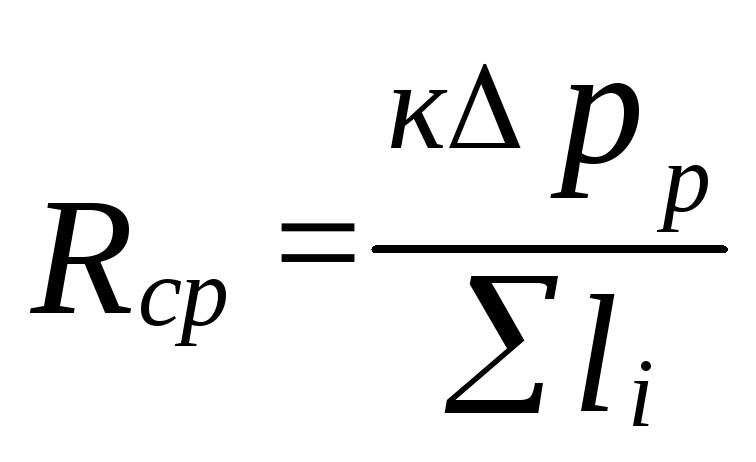
(5.4)
ที่ไหน
k=0.65 กำหนดสัดส่วนของการสูญเสียแรงดัน
สำหรับแรงเสียดทาน
5.
การไหลของน้ำในพื้นที่ถูกกำหนดโดย
สูตร
 (5.5)
(5.5)
ที่ไหน
คิว
- ภาระความร้อนบนไซต์ W:
(tจี
— tอู๋)
- ความแตกต่างของอุณหภูมิของน้ำหล่อเย็น
6.
ตามขนาด
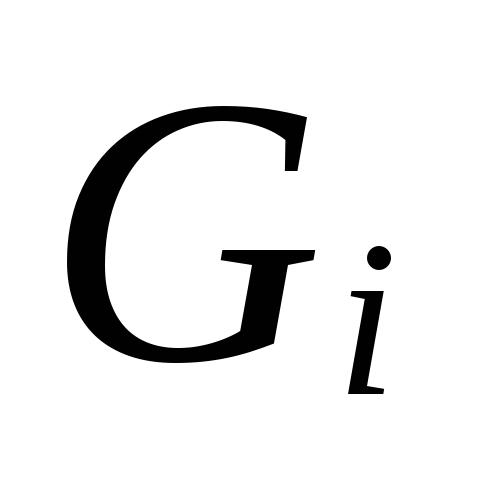
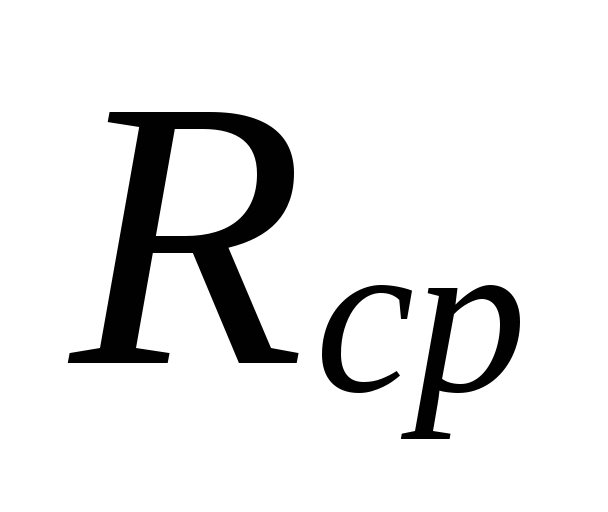
.

6.
สำหรับเส้นผ่านศูนย์กลางท่อที่เลือก
และกำหนดปริมาณการใช้น้ำโดยประมาณ
ความเร็วน้ำหล่อเย็น วี
และความเฉพาะเจาะจงที่แท้จริง
การสูญเสียความดันแรงเสียดทาน Rฉ.
ที่
การเลือกขนาดเส้นผ่านศูนย์กลางในพื้นที่ที่มีขนาดเล็ก
อัตราการไหลของน้ำหล่อเย็นสามารถ
ความแตกต่างใหญ่ระหว่าง
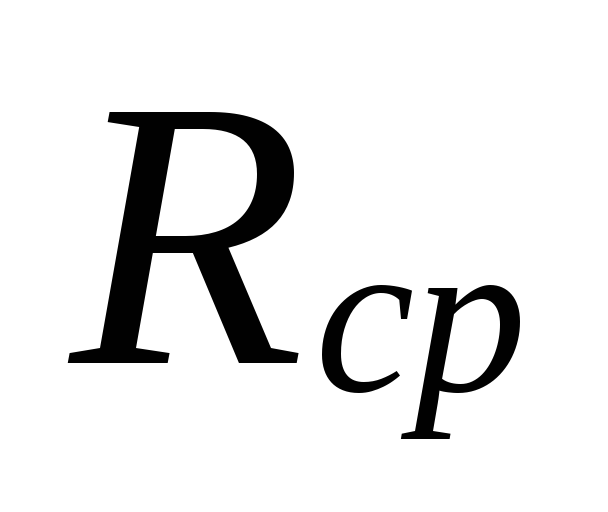
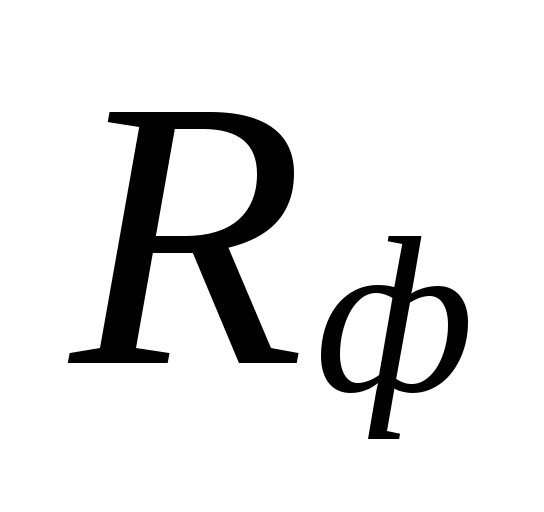
ประเมินความสูญเสียต่ำไป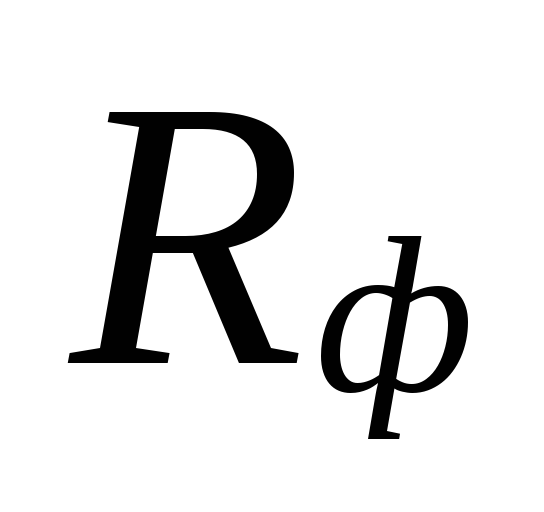
พื้นที่เหล่านี้ได้รับการชดเชยด้วยการประเมินค่าสูงไป
ปริมาณ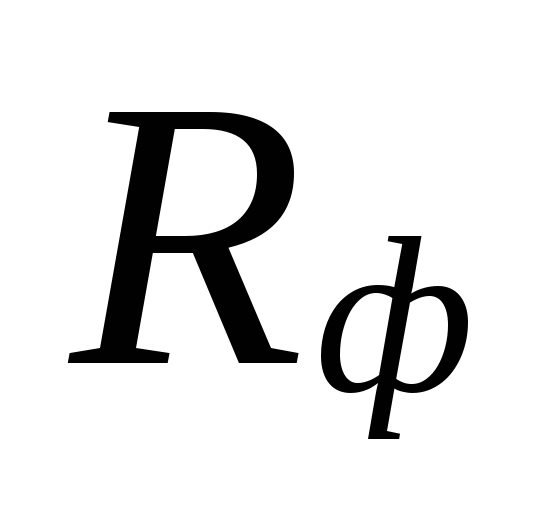
7.
การสูญเสียแรงดันแรงเสียดทานถูกกำหนด
บนพื้นที่คำนวณ ป่า:
 .
.
(5.6)
ผล
การคำนวณถูกป้อนในตารางที่ 5.2
8.
การสูญเสียแรงดันในท้องถิ่น
ความต้านทานโดยใช้สูตรอย่างใดอย่างหนึ่ง:
 ,
,
(5.7)
ที่ไหน
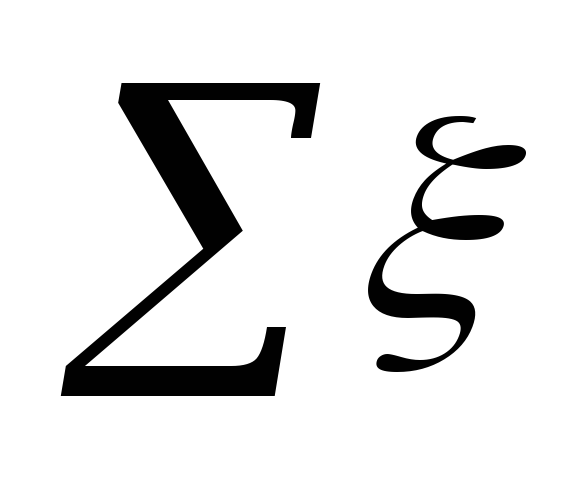
ในพื้นที่นิคม
ความหมาย ξ
ในแต่ละไซต์จะสรุปไว้ในตาราง 5.3.
ตารางที่ 5.3 -
ค่าสัมประสิทธิ์ความต้านทานท้องถิ่น
|
เลขที่ p / p |
ชื่อ |
ค่านิยม |
หมายเหตุ |
9.
กำหนดการสูญเสียแรงดันทั้งหมด
ในทุกพื้นที่
 .
.
(5.8)
10. กำหนด
การสูญเสียแรงดันทั้งหมดเนื่องจากแรงเสียดทานและ
ในการต่อต้านท้องถิ่นในหลัก
แหวนหมุนเวียน
 .
.
(5.9)
11. เปรียบเทียบ Δr
กับ ΔrR.
การสูญเสียแรงดันทั่วทั้งวงแหวน
ต้องน้อยกว่า ΔrR
บน
 .
.
(5.10)
สต็อกของใช้แล้วทิ้ง
ความดันเป็นสิ่งจำเป็นสำหรับ in
การคำนวณความต้านทานไฮดรอลิก
หากไม่เป็นไปตามเงื่อนไข
ถูกดำเนินการ มันเป็นสิ่งจำเป็นในบางส่วน
ส่วนของวงแหวนเพื่อเปลี่ยนขนาดเส้นผ่านศูนย์กลางของท่อ
12. หลังการคำนวณ
วงแหวนหมุนเวียนหลัก
ทำการเชื่อมโยงของวงแหวนที่เหลือ วี
แต่ละวงนับใหม่เท่านั้น
พื้นที่ไม่ส่วนกลางเพิ่มเติม
เชื่อมต่อแบบขนานกับส่วนต่างๆ
แหวนหลัก.
ความคลาดเคลื่อนของการสูญเสีย
แรงกดดันต่อการเชื่อมต่อแบบขนาน
แปลงได้ถึง 15% กับทางตัน
การเคลื่อนไหวของน้ำและมากถึง 5% - เมื่อผ่าน
ตาราง
5.2 - ผลการคำนวณไฮดรอลิก
สำหรับระบบทำความร้อน
|
บน |
โดย |
โดย |
||||||||||||||
|
ตัวเลข |
ความร้อน |
การบริโภค |
ความยาว |
เส้นผ่านศูนย์กลาง |
ความเร็ว |
เฉพาะเจาะจง |
ขาดทุน |
ซำ |
ขาดทุน |
d, |
วี, |
R, |
Δrtr, |
∑ξ |
Z, |
Rl+Z, |
บทที่ 6
การเปลี่ยนแปลงของอุณหภูมิก๊าซตามความยาวของท่อส่งก๊าซ
ในการไหลของก๊าซคงที่มวล
อัตราการไหลในท่อส่งก๊าซคือ
 . (2.41)
. (2.41)
อันที่จริงการเคลื่อนที่ของก๊าซในท่อส่งก๊าซ
ไม่เป็นอุณหภูมิความร้อนเสมอ วี
ในระหว่างการอัดแก๊สจะร้อนขึ้น
แม้จะเย็นลงที่ COP แล้ว อุณหภูมิ
ก๊าซเข้าสู่ท่อ
คือประมาณ2040С,
ซึ่งสูงกว่าอุณหภูมิมาก
สิ่งแวดล้อม (T).
ในทางปฏิบัติ อุณหภูมิของก๊าซจะกลายเป็น
ใกล้เคียงกับอุณหภูมิแวดล้อม
สำหรับท่อส่งก๊าซขนาดเล็กเท่านั้น
(Dy0.
นอกจากนี้ ควรคำนึงว่า
ท่อส่งก๊าซ
เป็นก๊าซจริงซึ่งมีอยู่ในตัว
เอฟเฟกต์ Joule-Thompson ซึ่งคำนึงถึง
การดูดซับความร้อนระหว่างการขยายตัวของก๊าซ
เมื่ออุณหภูมิเปลี่ยนแปลงไปตามความยาว
มีการอธิบายการเคลื่อนที่ของก๊าซในท่อส่งก๊าซ
ระบบสมการ:
พลังงานจำเพาะ ,
,
ความต่อเนื่อง ,
,
รัฐ ,
,
สมดุลความร้อน .
.
พิจารณาในการประมาณสมการแรก
สมดุลความร้อนโดยไม่คำนึงถึงผลกระทบ
จูล ทอมป์สัน. การบูรณาการสมการ
สมดุลความร้อน
 ,
,
เราได้รับ
 , (2.42)
, (2.42)
ที่ไหน ;
;
KSR- ค่าเฉลี่ยบนเว็บไซต์เต็ม
ค่าสัมประสิทธิ์การถ่ายเทความร้อนจากแก๊สถึง
สิ่งแวดล้อม;
G คืออัตราการไหลของมวลของก๊าซ
คพี–
ความจุความร้อนไอโซบาริกเฉลี่ยของก๊าซ
ค่าtL เรียกว่า เกณฑ์ไร้มิติ
ชูคอฟ
 (2.43)
(2.43)
ดังนั้นอุณหภูมิของแก๊สในตอนท้าย
ท่อส่งก๊าซจะเป็น
 . (2.44)
. (2.44)
ที่ระยะทาง x จากจุดเริ่มต้น
กำหนดอุณหภูมิของท่อส่งก๊าซ
ตามสูตร
 . (2.45)
. (2.45)
การเปลี่ยนแปลงของอุณหภูมิตามความยาวของท่อส่งก๊าซ
เป็นเลขชี้กำลัง (รูปที่
2.6).
พิจารณา
ผลของการเปลี่ยนแปลงอุณหภูมิของแก๊สต่อ
ประสิทธิภาพของท่อ
การคูณทั้งสองข้างของสมการจำเพาะ
พลังงานบน 2 และแสดง ,
,
เราได้รับ
 . (2.46)
. (2.46)
เราแสดงความหนาแน่นของก๊าซทางด้านซ้าย
นิพจน์ (2.46) จากสมการสถานะ
 ,
,
ผลิตภัณฑ์wจากสมการความต่อเนื่อง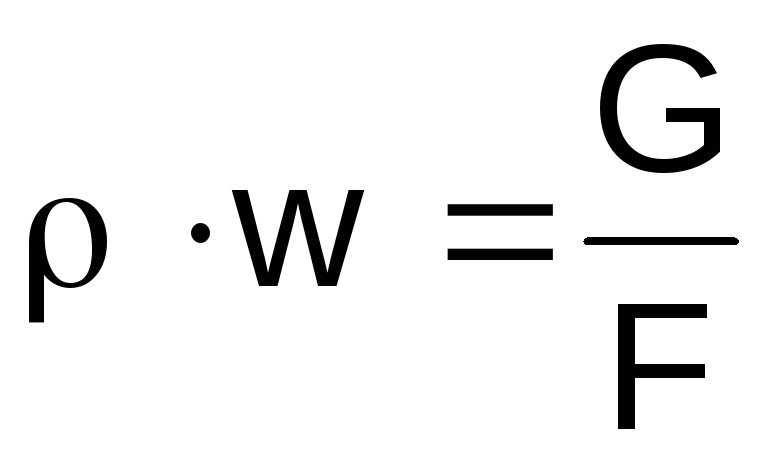
สมดุล .
.
ด้วยเหตุนี้ สมการจำเพาะ
พลังงานอยู่ในรูป
 (2.47)
(2.47)
หรือ
 . (2.48)
. (2.48)
แสดงถึง
 และรวมทางด้านซ้ายของสมการ
และรวมทางด้านซ้ายของสมการ
(2.48) จากพี่ชมdoPถึงและไปทางขวาจาก Tชมดอทถึง, เราได้รับ
 . (2.49)
. (2.49)
โดยแทนที่
 , (2.50)
, (2.50)
เรามี
 . (2.51)
. (2.51)
หลังจากรวมเข้ากับที่ระบุ
ขีดจำกัด เราได้รับ

 . (2.52)
. (2.52)
โดยคำนึงถึง (2.42)

หรือ
 , (2.53)
, (2.53)
ที่ไหน เป็นปัจจัยแก้ไขที่คำนึงถึง
เป็นปัจจัยแก้ไขที่คำนึงถึง
อุณหภูมิเปลี่ยนแปลงตามความยาวของท่อส่งก๊าซ
(ไม่ใช่ไอโซเทอร์มาลิตี้ของการไหลของก๊าซ)
โดยคำนึงถึง (2.53) การพึ่งพาอาศัยในการพิจารณา
อัตราการไหลของมวลของก๊าซจะอยู่ในรูป
 . (2.54)
. (2.54)
ความคุ้มค่า ชมมากกว่าหนึ่งเสมอ ดังนั้น
อัตราการไหลของมวลของก๊าซเมื่อมีการเปลี่ยนแปลง
อุณหภูมิตามความยาวของท่อส่งก๊าซ
(ระบบการไหลแบบไม่มีไอโซเทอร์มอล) เสมอ
น้อยกว่าในโหมดอุณหภูมิความร้อน
(ท=เดม). สินค้า Tชมเรียกว่า อินทิกรัลเฉลี่ย
อุณหภูมิของก๊าซในท่อ
ด้วยค่าของหมายเลข Shukhov Shu4
การไหลของก๊าซในท่อ
พิจารณาเกือบ isothermal
ที่ T=idem อุณหภูมิดังกล่าว
เป็นไปได้เมื่อปั๊มแก๊สด้วย
ต้นทุนท่อส่งก๊าซต่ำ
เส้นผ่านศูนย์กลางขนาดเล็ก (น้อยกว่า 500 มม.) เป็นนัยสำคัญ
ระยะทาง.
ผลของการเปลี่ยนแปลงอุณหภูมิของแก๊ส
แสดงออกถึงคุณค่าของหมายเลข Shukhov
ชู
ที่
ปั๊มแก๊สการปรากฏตัวของเค้น
ผลนำไปสู่ความลึก
ระบายความร้อนด้วยแก๊สมากกว่าการแลกเปลี่ยนความร้อนเท่านั้น
ด้วยดิน. ในกรณีนี้อุณหภูมิ
ก๊าซสามารถลดลงได้ด้านล่าง
อุณหภูมิ T (รูปที่
2.7).
ข้าว. 2.7. อิทธิพลของเอฟเฟกต์จูล-ทอมป์สัน
เกี่ยวกับการกระจายอุณหภูมิของแก๊สเกิน
ความยาวท่อ
1 - โดยไม่คำนึงถึง Di; 2 - กับ
โดยคำนึงถึง Di
จากนั้นพิจารณาสัมประสิทธิ์จูล-ทอมป์สัน
กฎของอุณหภูมิเปลี่ยนแปลงไปตามความยาว
ใช้แบบฟอร์ม
 , (2.55)
, (2.55)
5 การสูญเสียไฮดรอลิก
ความแตกต่าง
แรงดันน้ำมันในสองส่วนของหนึ่ง
และท่อเดียวกัน โดยมีเงื่อนไขว่า
ที่แรกตั้งอยู่ต้นน้ำและ
ที่สอง - ด้านล่างถูกกำหนด สมการ
เบอร์นูลลี
 ,
,
ที่ไหน
ชม2
- ชม1
- ความแตกต่างของความสูงของจุดศูนย์ถ่วง
ส่วนจากการเลือกโดยพลการ
ระดับแนวนอน
วี1,
วี2
– ความเร็วเฉลี่ยของน้ำมันในส่วน;
g - แรงเร่ง
แรงโน้มถ่วง;

การสูญเสียไฮดรอลิกระหว่างการเคลื่อนไหว
น้ำมันจากส่วนแรกไปส่วนที่สอง
สมการ
Bernoulli ใช้งานเต็มที่
สำหรับการคำนวณสายดูดของปั๊ม
ในกรณีอื่นๆ เทอมแรก
มักจะละเลยและถือว่า:

ไฮดรอลิค
การสูญเสียมักจะแบ่งออกเป็นท้องถิ่น
การสูญเสียและการสูญเสียความเสียดทานตามความยาว
ท่อ (เชิงเส้น)
1.5.1
การสูญเสียในท้องถิ่น
พลังงานเกิดจากท้องถิ่น
ความต้านทานไฮดรอลิก,
ทำให้เกิดการบิดเบือนการไหล ท้องถิ่น
ความต้านทานคือ: การหดตัว,
การขยายตัว, การปัดเศษของท่อ,
ตัวกรอง อุปกรณ์ควบคุม และ
ระเบียบ ฯลฯ เมื่อไหล
ของเหลวผ่านการต้านทานในท้องถิ่น
ความเร็วของมันเปลี่ยนไปและมักจะมี
กระแสน้ำวนขนาดใหญ่
ขาดทุน
แรงกดดันจากแนวต้านในท้องถิ่น
กำหนดโดยสูตร Weisbach:
 MPa
MPa
(หรือ
 ป้า),
ป้า),
ที่ไหน

การสูญเสีย,
วี
คือความเร็วการไหลเฉลี่ยเหนือหน้าตัด
ในท่อหลังความต้านทานในพื้นที่ m/s;
,
N/m3;
ก.=9.81 ม./วินาที2
แต่ละ
การต่อต้านในท้องถิ่นมีลักษณะเฉพาะ
โดยค่าสัมประสิทธิ์ของมัน

ด้วยกระแสความปั่นป่วน ค่า
ต้านทานและเปลี่ยนแปลงน้อยมาก
ด้วยการเปลี่ยนแปลงขนาดของส่วนความเร็ว
การไหลของของเหลวและความหนืด ดังนั้น
ถือว่าไม่ขึ้นกับจำนวน
เรโนลส์ รี
ค่านิยม

ตัวอย่างเช่นสำหรับทีออฟเดียวกัน
เส้นผ่านศูนย์กลางของช่องจะเท่ากัน
ถ้า:
ลำธาร
เพิ่ม, แตกต่าง; ไหล
ผ่าน;









ที่
ดัดท่อ

ค่านิยม

ในระบบไฮดรอลิกของอุปกรณ์ นำมาจาก
วรรณกรรมอ้างอิง
ที่
ไหลลื่น (Re
ขาดทุน
แรงกดดันจากแนวต้านในพื้นที่ที่
การไหลของลามิเนตถูกกำหนดโดย
สูตร:
 MPa
MPa
ที่ไหน

= อะ

ปริมาณ
การสูญเสียแรงดันในมาตรฐาน
อุปกรณ์ไฮดรอลิกสำหรับ
อัตราการไหลปกติ
ระบุไว้ในข้อกำหนดทางเทคนิค
1.5.2
ขาดทุน
แรงเสียดทานความยาว
คือการสูญเสียพลังงานที่เกิดขึ้น
ในท่อตรงที่มีหน้าตัดคงที่
เหล่านั้น. ด้วยการไหลของของเหลวสม่ำเสมอ
และเพิ่มสัดส่วนตามความยาว
ท่อ. การสูญเสียเหล่านี้เกิดจากภายใน
แรงเสียดทานในของเหลว ดังนั้นจึงมี
วางในท่อทั้งหยาบและเรียบ
ขาดทุน
ความดันแรงเสียดทานของท่อ
ถูกกำหนดโดยสูตร ดาร์ซี่:
 MPa
MPa
ที่ไหน

l
และ d
- ความยาวและเส้นผ่านศูนย์กลางภายในของท่อ
มม.
นี้
สูตรนี้ใช้ได้กับทั้งลามิเนต,
เช่นเดียวกับในกระแสน้ำปั่นป่วน ความแตกต่าง
ประกอบด้วยค่าสัมประสิทธิ์เท่านั้น

ที่
ไหลลื่น (Re
ที่
ค่าสัมประสิทธิ์การไหลปั่นป่วนของแรงเสียดทาน
ไม่ได้เป็นเพียงหน้าที่ของ Re แต่
ก็ขึ้นอยู่กับความหยาบของภายในด้วย
พื้นผิวท่อ สำหรับ ไฮดรอลิค
เรียบ ท่อ,
เหล่านั้น. ที่มีความหยาบกร้านนั้น
ในทางปฏิบัติไม่ส่งผลกระทบต่อความต้านทาน
ค่าสัมประสิทธิ์แรงเสียดทานปั่นป่วน
โหมดสามารถกำหนดได้โดยสูตร พีซี
โคนาโคว่า:

ท่อ
ถือว่าราบเรียบแบบไฮดรอลิกถ้า
(d/k)>(Re/20),
โดยที่ k คือความหยาบเท่ากัน
มม. ตัวอย่างเช่น สำหรับเหล็กไร้ตะเข็บใหม่
ท่อ k≈0.03
มม. และหลังจากใช้งานมาหลายปี
k≈0.2
มม. สำหรับท่อไร้รอยต่อใหม่ที่ทำจาก
โลหะที่ไม่ใช่เหล็ก k≈0.005
มม. ท่อเหล่านี้มักใช้ใน
ระบบไฮดรอลิกของเครื่องจักร
ค่าสัมประสิทธิ์
แรงเสียดทานในระบอบการปกครองที่ปั่นป่วนสามารถ
กำหนดโดยสูตร Altshulya,
เป็นสากล (เช่น ใช้บังคับ
ไม่ว่ากรณีใด ๆ):

2. ลักษณะการไหลของโมดูลการไหลของไปป์ไลน์
จำไว้นะ
สูตรการสูญเสียเชิงเส้น - สูตรดาร์ซี
- ไวส์บาค:
 .
.
ด่วน
ในสูตรนี้ ความเร็ว V
ผ่านกระแสQ
จากอัตราส่วน
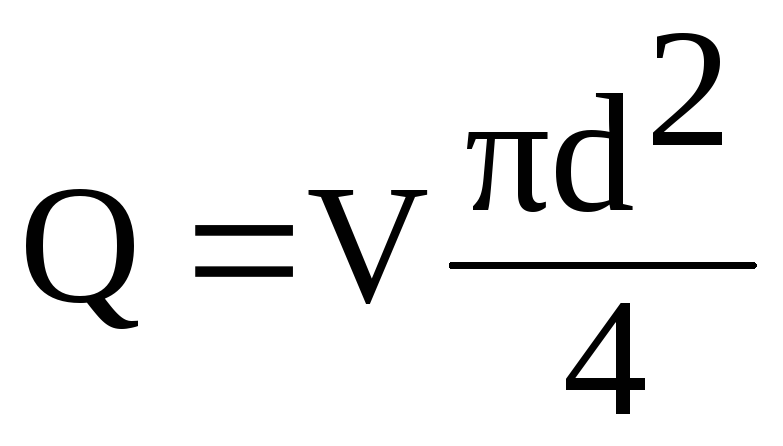
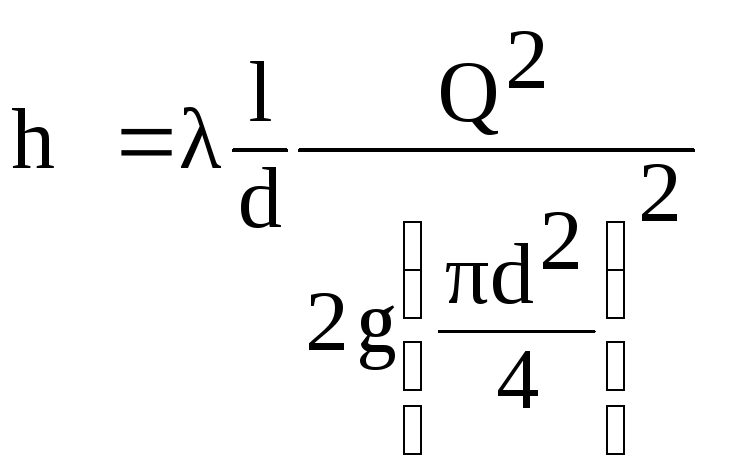
(6.1)
สำหรับ
ท่อที่มีเส้นผ่านศูนย์กลางที่กำหนด
ความซับซ้อนของปริมาณ
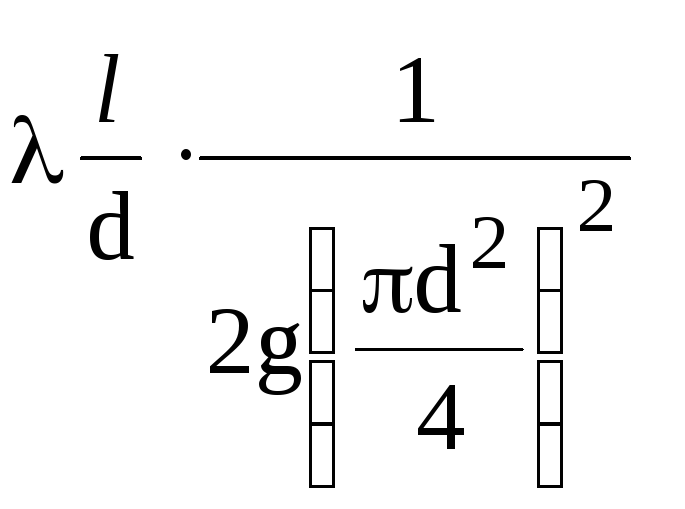
ค่าคงที่ (1/K2),
ยกเว้นค่าสัมประสิทธิ์ไฮดรอลิก
แรงเสียดทาน λ ตามแนวคิด
ความเร็วเศรษฐกิจเฉลี่ย Vs.e
ให้เราแสดงว่าสัมประสิทธิ์ที่ระบุ λ
สามารถนำมาประกอบกับความซับซ้อนนี้ได้เพราะ วี
ในกรณีนี้ หมายเลข Reynolds จะเป็น
มีความหมายเฉพาะ:
 ,
,
และบนพล็อต Nikuradze สัมประสิทธิ์ λ ใน
กรณีนี้จะมีความเฉพาะเจาะจง
ความหมาย.
ให้เหตุผล
ความถูกต้องของการแนะนำแนวคิด
ความเร็วเศรษฐกิจเฉลี่ยดังนี้
การให้เหตุผล
ไฮดรอลิค
ระบบต่างๆ เช่น ประปา,
คุณสามารถข้ามค่าใช้จ่ายบางอย่างได้
ทำจากท่อขนาดต่างๆ ที่
ในเวลาเดียวกัน เมื่อเส้นผ่านศูนย์กลาง d เพิ่มขึ้น
จึงทำให้ความเร็ว V . ลดลง
รายจ่ายฝ่ายทุนจะเพิ่มขึ้นและ
ค่าใช้จ่ายในการดำเนินงานจะ
ลดลงเนื่องจากการลดลงของไฮดรอลิก
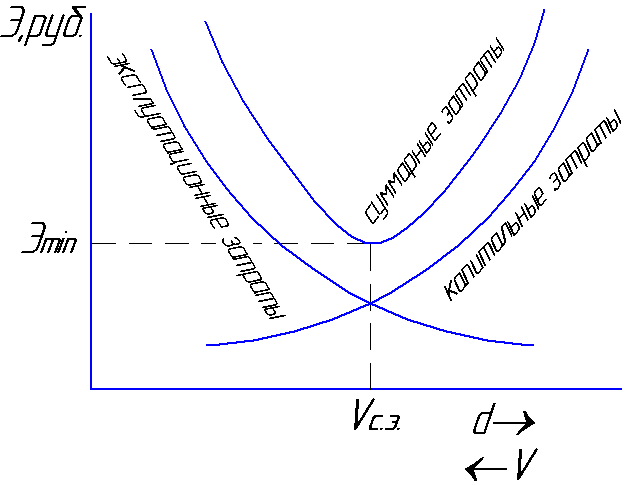
ความสูญเสีย ความเร็วที่ยอดรวม
ค่าใช้จ่ายจะน้อยที่สุด
จะเรียกว่าเศรษฐกิจเฉลี่ย
ความเร็ว Vs.e
= 0.8 ... 1.3 m / s (รูปที่ 6.1)
รูปที่ 6.1
แล้ว
สูตรการสูญเสียเชิงเส้น (6.1) ใช้รูปแบบ
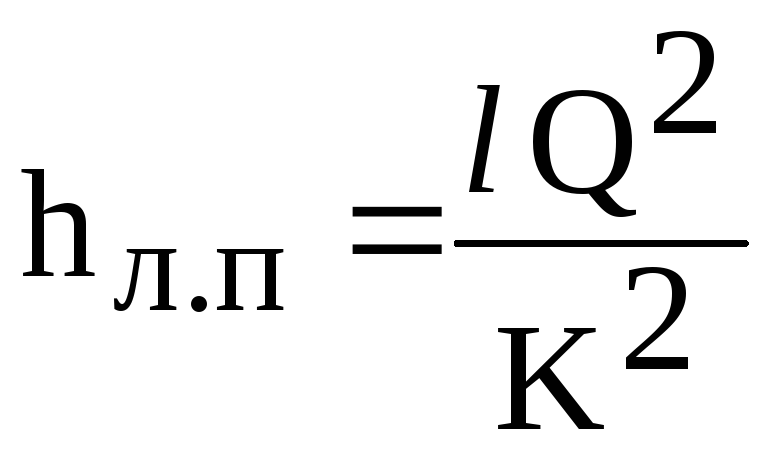
(6.2)
ที่ไหน
K - ลักษณะการไหลของท่อ
(โมดูลัสการไหล) ขึ้นอยู่กับวัสดุ
ท่อขนาดเส้นผ่านศูนย์กลางและการไหล ถูกถ่าย
จากตาราง
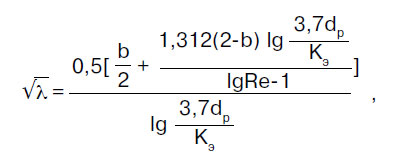
 ),ค
),ค ,
,