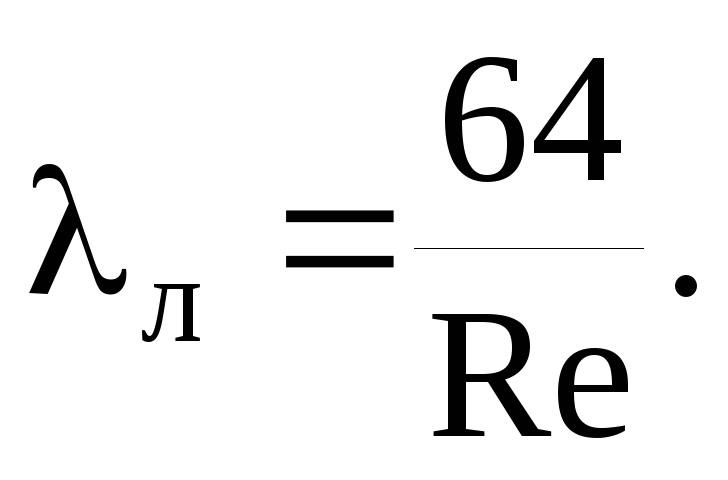1. Hidrostatik basınç
hidrostatik basınç
nedeniyle iç basınç kuvveti
uygulanan dış kuvvetlerin etkisiyle
sıvıda verilen nokta. Bu tür basınç
her yöne aynıdır ve bağlıdır
Duran bir sıvıdaki bir noktanın konumu hakkında.
Hidrostatik basıncın boyutu
MKGSS sisteminde - kg / cm2 veya t / m2,
SI sisteminde - N/m2.
Temel birim oranları
baskı yapmak:
|
kg/cm2 |
N/m2 |
|
|
teknik atmosfer |
1 |
98066,5 |
|
milimetre su sütunu |
0,0001 |
9,80665 |
|
milimetre cıva |
0,00136 |
133,32 |
Pratik hesaplamalarda 1 teknik
atmosfer \u003d 1 kg / cm2 \u003d 10 m su. Sanat. =
735 mmHg Sanat. = 98070 N/m2.
Sıkıştırılamaz bir akışkan için
kuvvet altında dengede
yerçekimi, tam hidrostatik
nokta basıncı:
p=p+

p serbest üzerindeki basınç nerede
sıvı yüzey;

alan ile yükseklik h
bire eşit kesit;
h - daldırma derinliği
puan;

Bazı sıvılar için değerler
çözmede kullanılan özgül ağırlık
görevler ekte verilmiştir (sekme.
P-3).
Aşırı basıncın değeri
atmosferik (pa)
manometrik olarak adlandırılan veya
aşırı basınç:

Serbest yüzeydeki basınç ise
atmosfere eşit, sonra fazla
basınç pm=

Atmosferik basınç altında
miktara vakum denir:
rkaçık= pa- R.
Bu sorunların çoğuna çözüm
bölüm kullanımla ilgilidir
hidrostatiğin temel denklemi

nerede z koordinattır veya
nokta işareti.
1. Boru hatlarının hidrolik hesaplanması hakkında genel bilgiler
Hesaplarken
boru hatları düşünülüyor
sabit, düzgün basınç
herhangi bir sıvının hareketi
türbülanslı rejim, yuvarlak-silindirik
borular. Basınçlı borularda sıvı
baskı altında ve
kesitleri tamamen
dolu. boyunca sıvının hareketi
sonuç olarak boru hattı oluşur
başlangıcındaki baskının daha büyük olduğu gerçeği
Sonunda.
Hidrolik
belirlemek için hesaplama yapılır.
boru hattı çapı D
bilinen biriyle
atlama sağlamak için uzunluk
belirli bir akış hızı Q
veya kurmak
belirli bir çapta ve gerekli uzunlukta
basınç ve sıvı akışı. boru hatları
uzunluklarına ve desenlerine bağlı olarak
konumlar basit olarak ayrılmıştır
ve karmaşık. Basit boru hatlarına
olmayan boru hatlarını içerir.
uzunluk boyunca dallar, sabit
aynı masraf.
boru hatları
aynı çaptaki borulardan oluşur
tüm uzunluk boyunca veya farklı boruların bölümlerinden
çaplar ve uzunluklar. son durum
seri bağlantı anlamına gelir.
Basit boru hatları
yerel bir arsa ile uzunluğa bağlı olarak
dirençler kısa ve
uzun. kısa
boru hatları
vardır
yeterince kısa uzunlukta boru hatları,
hangi yerel direnişte
hidroliklerin %10'undan fazlasını oluşturur
uzunluk kaybı. Örneğin, şunları içerirler:
sifon boruları, emme
kanatlı pompaların boruları, sifonlar (basınç
yol setinin altındaki su boruları),
binaların ve yapıların içindeki boru hatları
vb.
uzun
boru hatları
aranan
boru hatları nispeten büyük
uzunluk boyunca kafa kaybının olduğu uzunluklar
önemli ölçüde yerel sayıca fazla
kayıplar. Yerel kayıplar
5'ten az
boru hattının uzunluğu boyunca kayıplar ve dolayısıyla
ihmal edilebilirler veya tanıtılabilirler
artan hidrolik hesaplamalar
1.05'e eşit katsayı
Uzun boru hatları sisteme girer
su tedarik şebekeleri, pompalama kanalları
istasyonlar, kanallar ve boru hatları
sanayi kuruluşları ve
tarımsal amaçlı ve
vb.
Karmaşık boru hatları
uzunluk boyunca farklı dalları var,
şunlar. boru hattı bir boru ağından oluşur
belirli çaplar ve uzunluklar. karmaşık
boru hatları ikiye ayrılır
paralel, çıkmaz (dallı),
halka (kapalı) boru hatları,
su şebekesine dahildir.
Hidrolik
boru hattı hesaplama olarak azaltılır
genellikle üç ana sorunu çözmek için:
-
tanım
boru hattı akışı Q,
biliniyorsa
baskı yapmak H,
uzunluk ben
ve çap D
boru hattı,
belirli yerel mevcudiyeti göz önüne alındığında
dirençler veya yokluklarında; -
tanım
gerekli basınç H,
geçiş güvenliğini sağlamak için gerekli
bilinen akış Q
boru hattı ile
uzun ben
ve çap D; -
tanım
boru hattı çapı D
ne zaman
bilinen baş değerler H,
masraf Q
ve uzunluk ben.
Akışkan akış hızı
burada q > tasarım akışkan akışı, m3/s;
- borunun canlı bölümünün alanı, m2.
Sürtünme direnci katsayısı λ, SP 40-102-2000 “Polimerik malzemelerden yapılmış su temini ve kanalizasyon sistemleri için boru hatlarının tasarımı ve montajı” kurallarının düzenlemelerine göre belirlenir. Genel Gereksinimler":
burada b, akışkan akış rejimlerinin bazı benzerlik sayısıdır; b > 2 için b = 2 alınır.
burada Re, gerçek Reynolds sayısıdır.
burada ν sıvının kinematik viskozite katsayısıdır, m²/s. Soğuk su boruları hesaplanırken, 1,31 10-6 m² / s'ye eşit alınır - +10 ° C sıcaklıktaki suyun viskozitesi;
Rekv > - Hidrolik direncin ikinci dereceden bölgesinin başlangıcına karşılık gelen Reynolds sayısı.
burada Ke, boru malzemesinin hidrolik pürüzlülüğüdür, m.Polimer malzemelerden yapılmış borular için, boru üreticisi başka pürüzlülük değerleri vermezse Ke = 0.00002 m alınır.
Re ≥ Rekv olduğu akış durumlarında, b parametresinin hesaplanan değeri 2'ye eşit olur ve formül (4) önemli ölçüde basitleştirilir ve iyi bilinen Prandtl formülüne dönüşür:
Ke = 0.00002 m'de, ikinci dereceden direnç bölgesi, kamusal su tedarik sistemlerinde pratik olarak ulaşılamayan 32.75 m/s'ye eşit bir su akış hızında (ν = 1.31 10-6 m²/s) meydana gelir.
Günlük hesaplamalar için nomogramlar önerilir ve daha doğru hesaplamalar için - "Polimerik malzemelerden yapılmış boru hatlarının hidrolik hesaplamaları için tablolar", cilt 1 "Basınç boru hatları" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
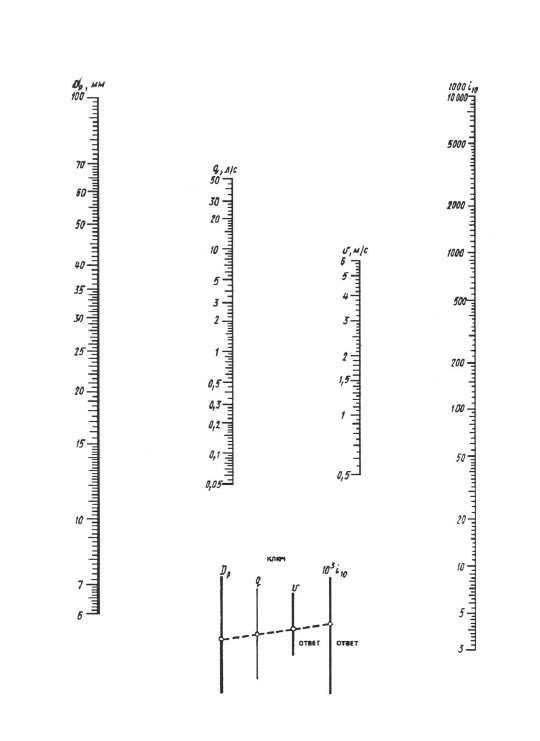
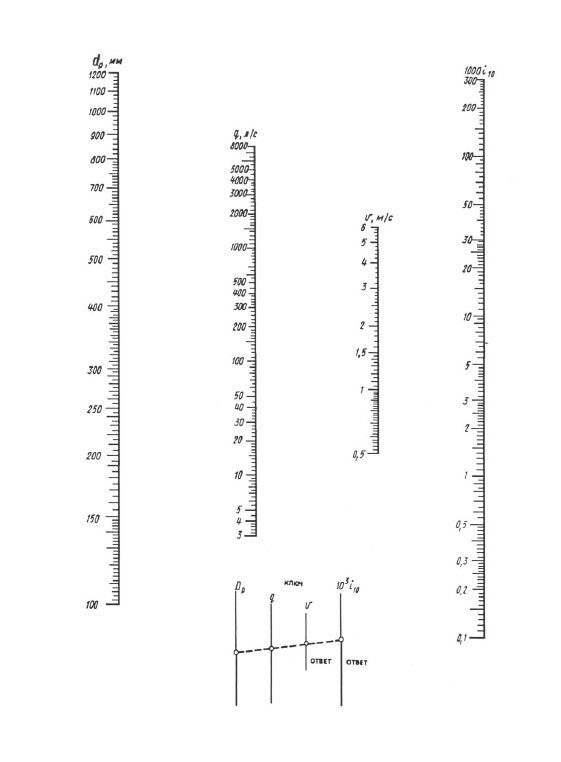
Nomogramlara göre hesaplarken, sonuç, cetvelin bir kaplaması ile elde edilir - dp ölçeğinde hesaplanan çapın değeri ile noktayı, q (l / l / s) düz bir çizgi ile ölçekleyin, bu düz çizgiyi, hız V ölçekleri ve 1000 i (mm/m) özgül kayıplar ölçekleriyle kesişene kadar devam ettirin. Düz bir çizginin bu ölçeklerle kesiştiği noktalar V ve 1000 i değerini verir.
Bildiğiniz gibi, sıvı pompalamak için elektriğin maliyeti H (ceteris paribus) değeri ile doğru orantılıdır. ( 3 ) ifadesini formül ( 2 ) ile değiştirerek, i (ve dolayısıyla H) değerinin, beşinci derece ile hesaplanan çap dp ile ters orantılı olduğunu görmek kolaydır.
Yukarıda dp değerinin boru duvarının e kalınlığına bağlı olduğu gösterilmiştir: duvar ne kadar ince olursa, dp o kadar yüksek olur ve buna bağlı olarak sürtünmeden kaynaklanan basınç kaybı ve elektrik maliyeti o kadar düşük olur.
Herhangi bir nedenle borunun MRS değeri değişirse çapı ve et kalınlığı (SDR) yeniden hesaplanmalıdır.
Bazı durumlarda, MRS 8'li borular, özellikle MRS 6.3'lü borular yerine MRS 10'lu boruların kullanılmasının, boru hattının çapını bir boyutta küçültmeyi mümkün kıldığı akılda tutulmalıdır. Bu nedenle, zamanımızda, boru üretimi için polietilen PE 63 (MRS 6.3) yerine polietilen PE 80 (MRS 8) ve PE 100 (MRS 10) kullanımı, yalnızca boruların duvar kalınlığını değil, ağırlıklarını da azaltmaya izin verir. ve malzeme tüketimi değil, aynı zamanda sıvı pompalamak için enerji maliyetlerini azaltmak (ceteris paribus).
Son yıllarda (2013'ten sonra), PE80 polietilenden imal edilen borular, üretimden neredeyse tamamen PE100 dereceli polietilenden imal edilen borularla değiştirilmiştir. Bu, boruların yapıldığı hammaddelerin PE100 markası ile yurt dışından tedarik edilmesi ile açıklanmaktadır.Ayrıca, polietilen 100 sınıfının, PE80'den yapılmış borularla aynı özelliklere sahip, ancak daha ince bir duvarla üretildiği ve böylece polietilen boru hatlarının verimini artırdığı için daha fazla mukavemet özelliklerine sahip olması nedeniyle.
6,100 mm çaplı borularda basınç kayıplarını belirlemek için nomogram.
100, 1200 mm çaplı borularda basınç kayıplarını belirlemek için nomogram.
Reynolds kriteri
Bu bağımlılık, İngiliz fizikçi ve mühendis Osborne Reynolds (1842-1912) tarafından ortaya çıkarıldı.
Viskoziteyi dikkate almaya gerek var mı sorusunun yanıtlanmasına yardımcı olan kriter Reynolds sayısı Re'dir. Akan bir akışkanın bir elemanının hareket enerjisinin iç sürtünme kuvvetlerinin çalışmasına oranına eşittir.
Kenar uzunluğu n olan bir kübik akışkan elemanı düşünün. Bir elementin kinetik enerjisi:
Newton yasasına göre, bir akışkan elemanına etkiyen sürtünme kuvveti şu şekilde tanımlanır:
Bu kuvvetin, bir akışkan elemanını n mesafesi boyunca hareket ettirirken yaptığı iş;
ve akışkan elemanın kinetik enerjisinin sürtünme kuvvetinin işine oranıdır.
Azaltıyoruz ve şunları elde ediyoruz:
Re, Reynolds sayısı olarak adlandırılır.
Böylece Re, viskoz kuvvetlerin göreceli rolünü karakterize eden boyutsuz bir niceliktir.
Örneğin, sıvı veya gazın temas ettiği cismin boyutları çok küçükse, düşük viskozitede bile Re önemsiz olacaktır ve sürtünme kuvvetleri baskın bir rol oynar. Aksine, cismin boyutları ve hızı büyükse, Re >> 1 ve hatta büyük bir viskozite bile hareketin doğası üzerinde neredeyse hiçbir etkiye sahip olmayacaktır.
Bununla birlikte, her zaman büyük Reynolds sayıları, viskozitenin herhangi bir rol oynamadığı anlamına gelmez. Böylece, Re sayısının çok büyük (birkaç on veya yüzbinlerce) değerine ulaşıldığında, pürüzsüz bir laminer (Latince laminadan - “plaka”) akış çalkantılı bir akışa (Latince türbülans - “fırtınalı” dan) dönüşür. , “kaotik”), kaotik, kararsız hareketlerin eşlik ettiği sıvılar. Bu etki, bir su musluğunu kademeli olarak açarsanız gözlemlenebilir: ince bir akış genellikle düzgün akar, ancak suyun hızındaki bir artışla akışın düzgünlüğü bozulur. Yüksek basınç altında dışarı akan bir jette, sıvı parçacıklar rastgele hareket eder, salınım yapar, tüm harekete güçlü karıştırma eşlik eder.
Türbülansın görünümü sürtünmeyi büyük ölçüde artırır. Bir boru hattında, türbülanslı akış hızı, aynı basınç düşüşlerinde laminer akış hızından daha azdır. Ancak türbülans her zaman kötü değildir. Türbülans sırasında karıştırmanın çok önemli olması nedeniyle, ısı transferi - agregaların soğutulması veya ısıtılması - çok daha yoğun bir şekilde gerçekleşir; kimyasal reaksiyonlar daha hızlı yayılır.
Bernoulli'nin Durağan Hareket Denklemi
Hidromekaniğin en önemli denklemlerinden biri 1738'de İsviçreli bilim adamı Daniel Bernoulli (1700-1782) tarafından elde edildi. İlk önce Bernoulli formülünde ifade edilen ideal bir sıvının hareketini tanımlamayı başardı.
İdeal bir akışkan, ideal bir akışkanın elemanları arasında ve ayrıca ideal akışkan ile kabın duvarları arasında hiçbir sürtünme kuvvetinin olmadığı bir akışkandır.
Adını taşıyan durağan hareket denklemi:
burada P sıvının basıncıdır, ρ yoğunluğudur, v hareket hızıdır, g serbest düşüşün ivmesidir, h sıvının elemanının bulunduğu yüksekliktir.
Bernoulli denkleminin anlamı, sıvı ile dolu bir sistemin (boru hattı bölümü) içinde her noktanın toplam enerjisinin her zaman değişmediğidir.
Bernoulli denkleminin üç terimi vardır:
- ρ⋅v2/2 - dinamik basınç - tahrik sıvısının birim hacmi başına kinetik enerji;
- ρ⋅g⋅h - ağırlık basıncı - birim hacimdeki sıvının potansiyel enerjisi;
- P - statik basınç, kökeninde basınç kuvvetlerinin işidir ve herhangi bir özel enerji türünün (“basınç enerjisi”) rezervini temsil etmez.
Bu denklem, borunun dar bölümlerinde akış hızının neden arttığını ve boru duvarlarındaki basıncın neden azaldığını açıklar. Borulardaki maksimum basınç, tam olarak borunun en büyük kesite sahip olduğu yerde ayarlanır. Borunun dar kısımları bu konuda güvenlidir ancak içlerindeki basınç o kadar düşebilir ki sıvı kaynar ve bu da boru malzemesinin kavitasyona ve tahribatına neden olabilir.
Viskoz sıvılar için Navier-Stokes denklemi
Daha titiz bir formülasyonda, viskoz sürtünmenin sıvı hızındaki değişime doğrusal bağımlılığı Navier-Stokes denklemi olarak adlandırılır. Sıvıların ve gazların sıkıştırılabilirliğini hesaba katar ve Newton yasasından farklı olarak, yalnızca katı bir cismin yüzeyinin yakınında değil, aynı zamanda sıvının her noktasında (sıkıştırılamaz durumda katı bir cismin yüzeyinin yakınında) geçerlidir. sıvı, Navier-Stokes denklemi ve Newton yasası çakışır).
Sürekli bir ortamın koşulunun sağlandığı herhangi bir gaz da Navier-Stokes denklemine uyar, yani. Newton akışkanlarıdır.
Sıvıların ve gazların viskozitesi genellikle nispeten düşük hızlarda önemlidir, bu nedenle bazen Euler hidrodinamiğinin Navier-Stokes hidrodinamiğinin yüksek hızlarının özel (sınırlayıcı) bir durumu olduğu söylenir.
Düşük hızlarda, Newton'un viskoz sürtünme yasasına göre, cismin sürükleme kuvveti hız ile orantılıdır. Yüksek hızlarda, viskozite önemli bir rol oynamayı bıraktığında, vücudun direnci hızın karesiyle orantılıdır (ilk olarak Newton tarafından keşfedilmiş ve doğrulanmıştır).
Hidrolik Hesap Sırası
1.
Ana sirkülasyon seçildi
halka ısıtma sistemi (çoğu
hidrolikte dezavantajlı bir şekilde konumlandırılmış
ilişki). Çıkmaz iki borulu
sistemler içinden geçen bir halkadır
en uzak cihazın alt enstrümanı ve
tek borulu yüklü yükseltici -
en uzak ve yüklü aracılığıyla
yükseltici.
Örneğin,
ile iki borulu bir ısıtma sisteminde
üst kablolama ana sirkülasyonu
halka ısı noktasından geçecek
ana yükseltici, besleme hattı aracılığıyla,
en uzak yükseltici aracılığıyla, ısıtma
alt kattaki cihaz, dönüş hattı
ısıtma noktasına.
V
ilişkili su hareketi olan sistemler
halka ana olarak alınır,
en ortasından geçen
yüklü stand.
2.
Ana sirkülasyon halkası kırılır
parsellere (arsa karakterize edilir
sabit su akışı ve aynı
çap). diyagram gösterir
bölüm numaraları, uzunlukları ve termal
yükler. Ana termal yük
parseller toplanarak belirlenir
bunlar tarafından sunulan termal yükler
araziler. Boru çapını seçmek için
iki miktar kullanılır:
a)
verilen su akışı;
B)
yaklaşık özgül basınç kayıpları
tasarım dolaşımındaki sürtünme için
yüzük revlenmek.
İçin
hesaplama rcp
ana uzunluğu bilmek gerekir
sirkülasyon halkası ve hesaplanan
dolaşım basıncı.
3.
hesaplanan sirkülasyon
formül basıncı
 ,
,
(5.1)
nerede
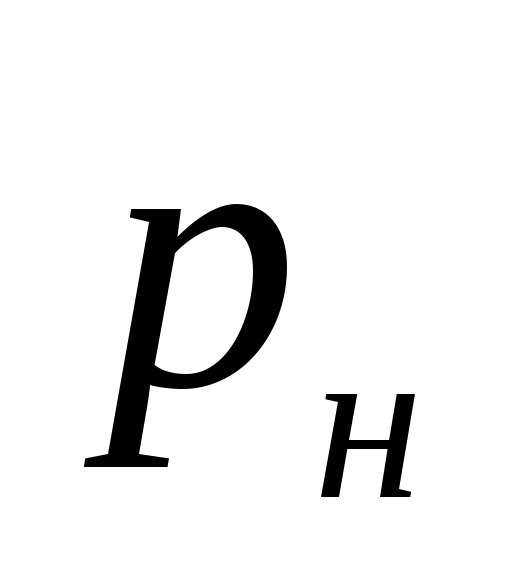
pompa tarafından oluşturulan basınç, Pa.
Sistem Tasarım Uygulaması
ısıtma gösterdi ki en
pompa basıncının alınması tavsiye edilir,
eşit
 ,
,
(5.2)
nerede
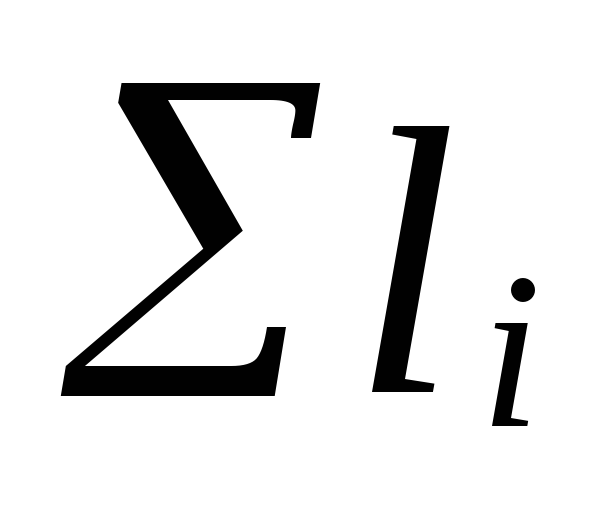
ana dolaşımın bölümlerinin uzunluklarının toplamı
yüzükler;
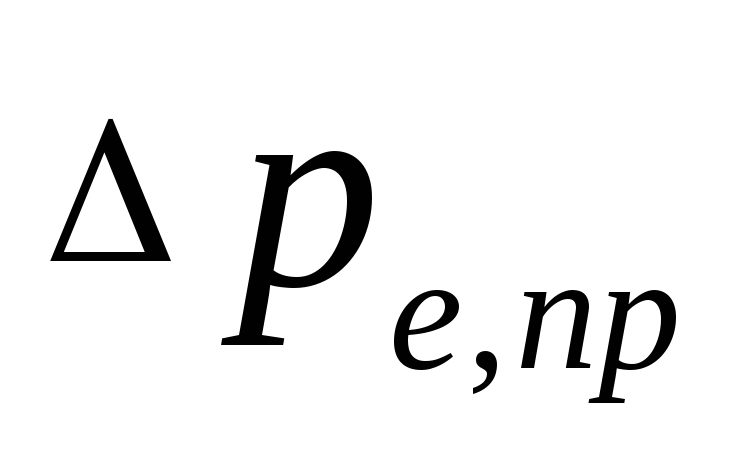
meydana gelen doğal basınç
cihazlarda su soğutma, Pa, mümkün
nasıl olduğunu belirlemek
 ,
,
(5.3)
nerede
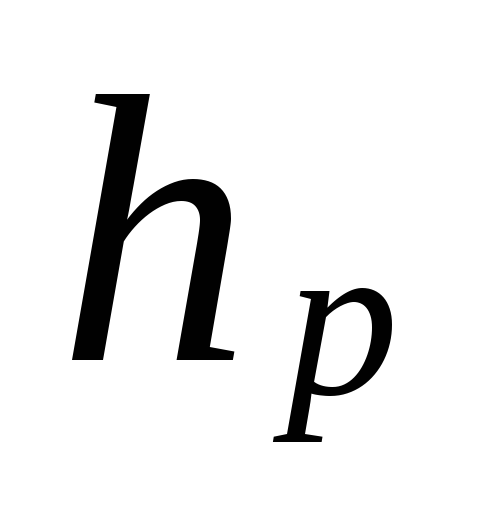
pompanın merkezine olan mesafe (asansör)
alt katın cihazının ortasına, m.
Anlam
katsayı mümkün
Tablo 5.1'den belirleyin.
tablo
5.1 - Anlamı c
tasarım sıcaklığına bağlı olarak
ısıtma sisteminde su
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
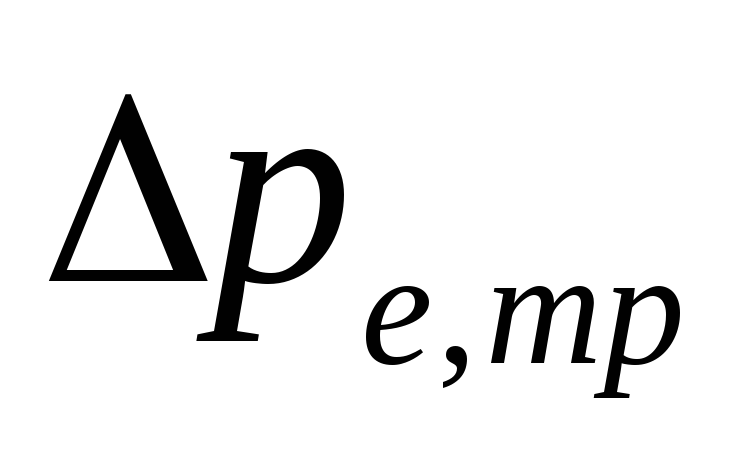
doğal basınç
boru hatlarında su soğutması sonucu
.
V
alt kablolamalı pompalama sistemleri
büyüklük
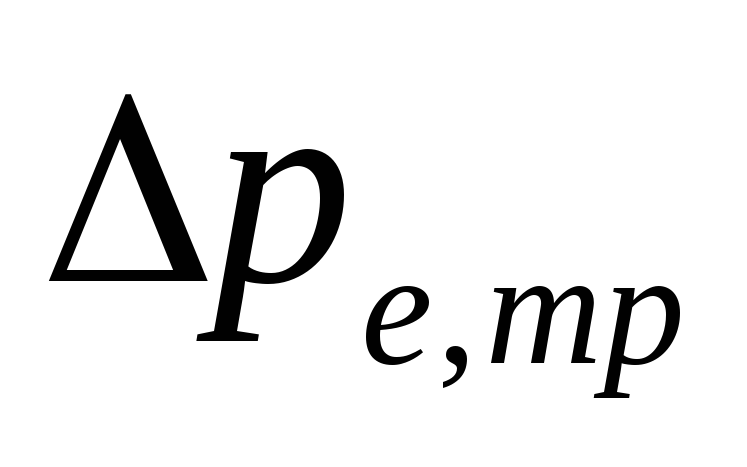
-
belirlenir
özgül sürtünme basıncı kaybı
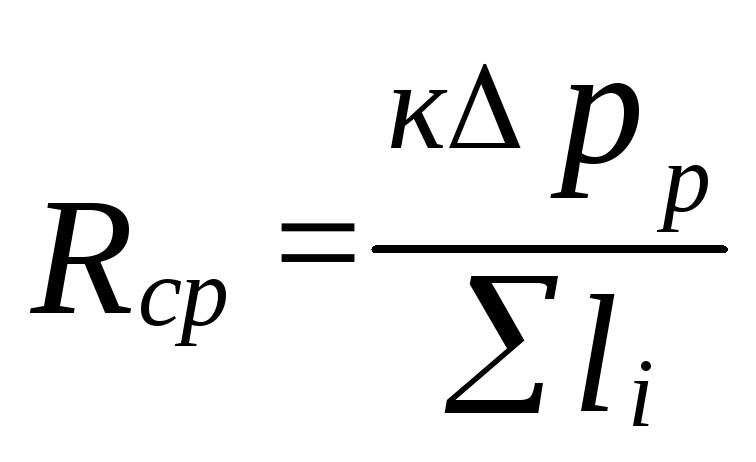
(5.4)
nerede
k=0.65, basınç kayıplarının oranını belirler
sürtünme için.
5.
Bölgedeki su akışı belirlenir.
formül
 (5.5)
(5.5)
nerede
Q
- sitedeki ısı yükü, W:
(TG
- TÖ)
- soğutucunun sıcaklık farkı.
6.
büyüklüğe göre
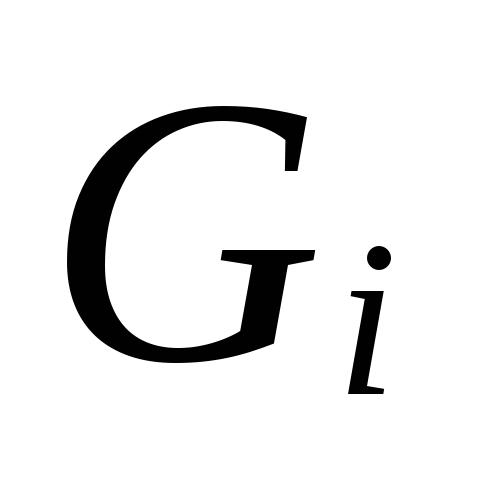
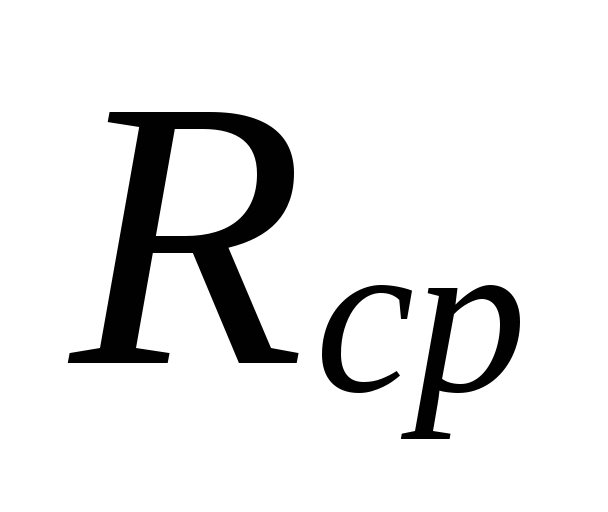
.

6.
Seçilen boru hattı çapları için
ve tahmini su tüketimi belirlenir
soğutucu hızı v
ve gerçek özel
sürtünme basıncı kaybı rF.
saat
küçük alanlarda çap seçimi
soğutucu akış hızları olabilir
arasında büyük farklılıklar
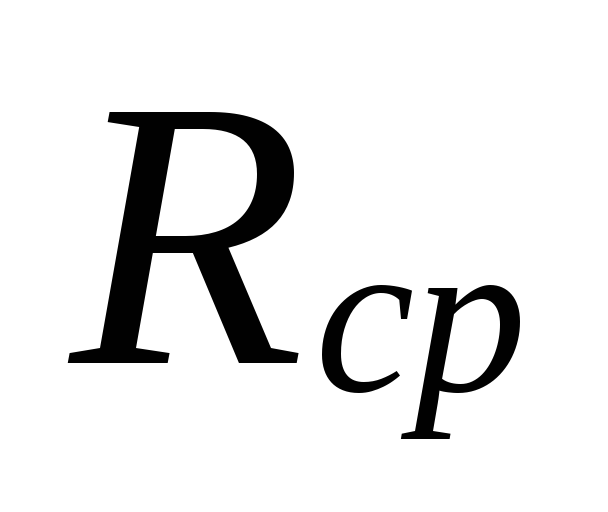
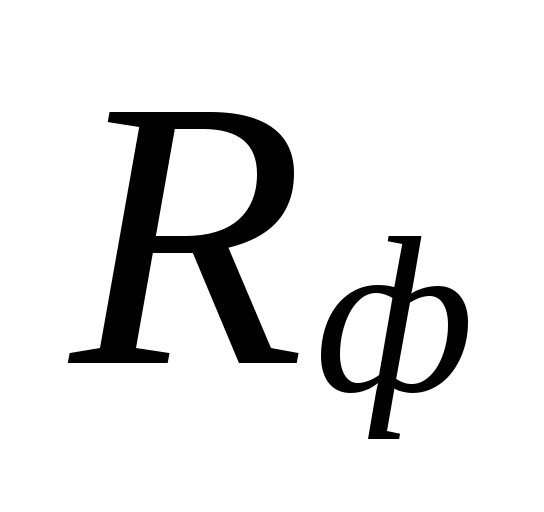
hafife alınan kayıplar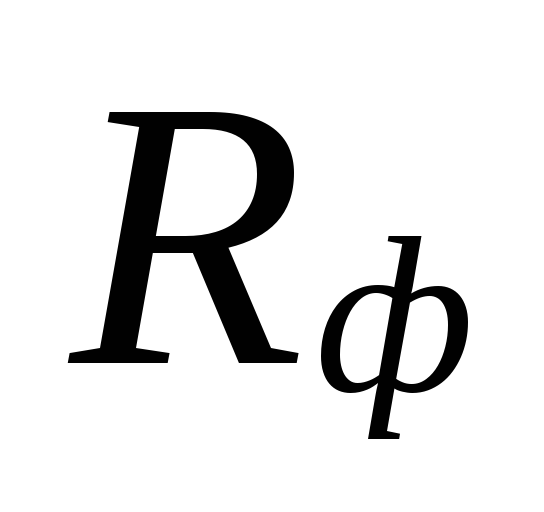
bu alanlar fazla tahmin ile telafi edilir
miktarları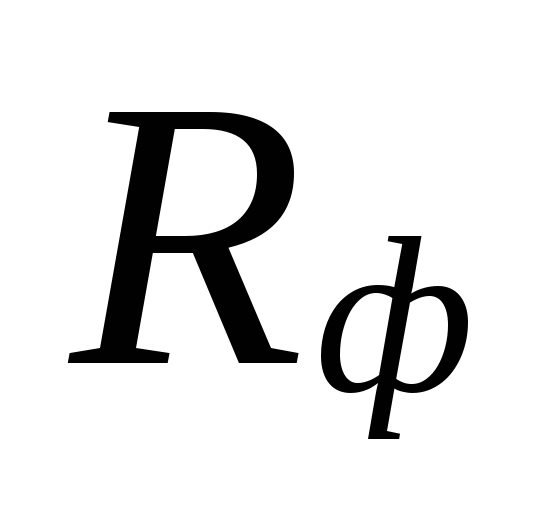
7.
Sürtünme basıncı kayıpları belirlenir
hesaplanan alanda, Pa:
 .
.
(5.6)
Sonuçlar
hesaplamalar Tablo 5.2'ye girilmiştir.
8.
Yerel basınç kayıpları
aşağıdaki formülü kullanarak dirençler:
 ,
,
(5.7)
nerede
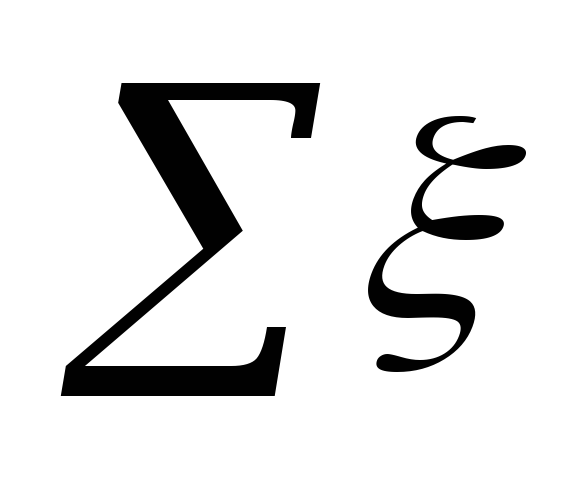
yerleşim bölgesinde.
Anlam ξ
her sitede tabloda özetlenmiştir. 5.3.
Tablo 5.3 -
Yerel direnç katsayıları
|
hayır. p / p |
İsimler |
değerler |
notlar |
9.
Toplam basınç kaybını belirleyin
her alanda
 .
.
(5.8)
10. Belirle
sürtünme nedeniyle toplam basınç kaybı ve
esas olarak yerel direnişlerde
sirkülasyon halkası
 .
.
(5.9)
11. Karşılaştır Δp
İle Δpr.
Halka boyunca toplam basınç kaybı
daha az olmalı Δpr
üzerinde
 .
.
(5.10)
tek kullanımlık stok
açıklanamayan için baskı gereklidir
hidrolik direncin hesaplanması.
şartlar uygun değilse
yapılır, bazılarında gereklidir
boruların çaplarını değiştirmek için halkanın bölümleri.
12. Hesaplamadan sonra
ana sirkülasyon halkası
kalan halkaların bağlantısını yapın. V
her yeni çalma sayısı yalnızca
ek ortak olmayan alanlar,
bölümlere paralel olarak bağlı
ana halka.
kayıp tutarsızlığı
paralel bağlı basınçlar
çıkmaz sokaklarla %15'e kadar izin verilen arsalar
suyun hareketi ve %5'e kadar - geçerek.
tablo
5.2 - Hidrolik hesaplama sonuçları
ısıtma sistemi için
|
Üzerinde |
İle |
İle |
||||||||||||||
|
Numara |
termal |
Tüketim |
Uzunluk |
Çap |
Hız |
Özel |
kayıplar |
toplam |
kayıplar |
D, |
v, |
r, |
Δptr, |
∑ξ |
Z, |
rl+Z, |
6. Ders
Gaz boru hattının uzunluğu boyunca gaz sıcaklığındaki değişiklik
Sabit gaz akışında, kütle
gaz boru hattındaki akış hızı
 . (2.41)
. (2.41)
Aslında, gaz boru hattındaki gazın hareketi
her zaman izotermal değildir. V
Sıkıştırma sırasında gaz ısınır.
COP'de soğutulduktan sonra bile, sıcaklık
boru hattına giren gaz
yaklaşık 2040С,
sıcaklıktan çok daha yüksek olan
çevre (T).
Pratikte, gazın sıcaklığı
ortam sıcaklığına yakın
sadece küçük çaplı gaz boru hatları için
(Dy0.
Ayrıca, dikkate alınmalıdır ki
boru hattı gaz
doğasında bulunan gerçek bir gazdır.
dikkate alan Joule-Thompson etkisi
gaz genleşmesi sırasında ısı emilimi.
Sıcaklık uzunluk boyunca değiştiğinde
gaz boru hattı gaz hareketi anlatılıyor
denklem sistemi:
spesifik enerji ,
,
süreklilik ,
,
devletler ,
,
ısı dengesi .
.
İlk yaklaşımda denklemi düşünün
etkisini hesaba katmadan ısı dengesi
Joule Thompson. denklemi entegre etme
ısı dengesi
 ,
,
alırız
 , (2.42)
, (2.42)
nerede ;
;
KSR- sitede ortalama dolu
gazdan ısı transfer katsayısı
Çevre;
G, gazın kütle akış hızıdır;
CP–
gazın ortalama izobarik ısı kapasitesi.
bir değerTL boyutsuz kriter olarak adlandırılır.
Şuhov
 (2.43)
(2.43)
Yani sonunda gaz sıcaklığı
doğalgaz boru hattı olacak
 . (2.44)
. (2.44)
Başlangıçtan x uzaklıkta
gaz boru hattı gaz sıcaklığı belirlenir
formüle göre
 . (2.45)
. (2.45)
Gaz boru hattının uzunluğu boyunca sıcaklıktaki değişiklik
üsteldir (Şek.
2.6).
Düşünmek
gaz sıcaklık değişiminin etkisi
boru hattı performansı.
Belirli bir denklemin her iki tarafını çarpma
2'deki enerji ve ifade ,
,
alırız
 . (2.46)
. (2.46)
Sol taraftaki gazın yoğunluğunu ifade ediyoruz
durum denkleminden ifadeler (2.46)
 ,
,
ürünw süreklilik denkleminden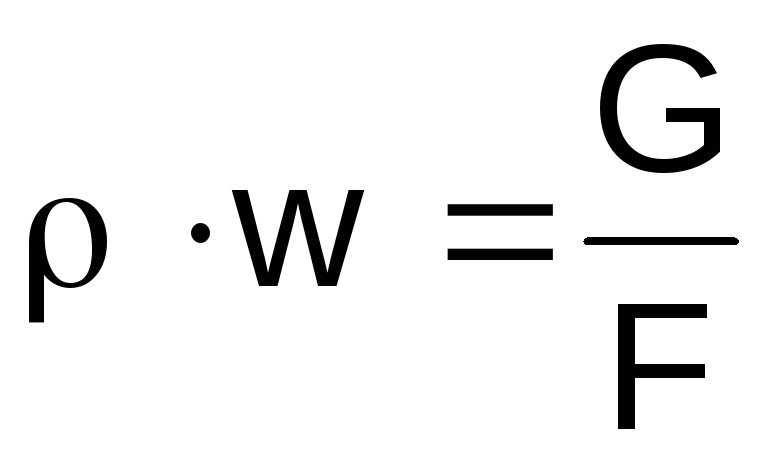
denge .
.
Bunu akılda tutarak, özel denklem
enerji şeklini alır
 (2.47)
(2.47)
veya
 . (2.48)
. (2.48)
ifade eden
 ve denklemin sol tarafını entegre etmek
ve denklemin sol tarafını entegre etmek
(2.48) P'denHdoPİLE, ve T'den sağaHnoktaİLE, alırız
 . (2.49)
. (2.49)
Değiştirerek
 , (2.50)
, (2.50)
sahibiz
 . (2.51)
. (2.51)
Belirtilen entegrasyondan sonra
limitler, elde ederiz

 . (2.52)
. (2.52)
(2.42) dikkate alındığında

veya
 , (2.53)
, (2.53)
nerede dikkate alan bir düzeltme faktörüdür
dikkate alan bir düzeltme faktörüdür
gaz boru hattının uzunluğu boyunca sıcaklık değişimi
(gaz akışının izotermal olmaması).
(2.53) dikkate alındığında, bağımlılığı belirleme
gazın kütle akış hızı şeklini alacak
 . (2.54)
. (2.54)
Değer Hher zaman birden büyüktür, yani
değiştirirken gazın kütle akış hızı
gaz boru hattının uzunluğu boyunca sıcaklık
(izotermal olmayan akış rejimi) her zaman
izotermal moddan daha az
(T=idem). Ürün THortalama integral denir
boru hattındaki gazın sıcaklığı.
Shukhov sayısının Shu4 değerleri ile
boru hattındaki gaz akışı
neredeyse izotermal düşünün
T=idem'de. Böyle bir sıcaklık
ile gaz pompalarken mod mümkündür
düşük gaz boru hattı maliyetleri
önemli bir küçük (500 mm'den az) çap
mesafe.
Değişen gaz sıcaklığının etkisi
Shukhov sayısının değerleri için kendini gösterir
Şu
saat
bir gaz kelebeğinin varlığını pompalayan gaz
etkisi daha derine yol açar
sadece ısı değişimi ile gaz soğutması
toprak ile. Bu durumda sıcaklık
gaz aşağıya bile düşebilir
sıcaklık T (Şek.
2.7).
Pirinç. 2.7. Joule-Thompson etkisinin etkisi
üzerinde gaz sıcaklık dağılımı üzerinde
boru hattı uzunluğu
1 - Di'yi hesaba katmadan; 2 - ile
Di'yi dikkate alarak
Daha sonra Joule-Thompson katsayısı dikkate alınarak
uzunluk boyunca sıcaklık değişimi yasası
formu alır
 , (2.55)
, (2.55)
5 Hidrolik kayıplar
Fark
yağ basıncı tek parçanın iki bölümünde
ve aynı boru hattı, şartıyla
ilki akış yukarısında bulunur ve
ikinci - aşağıda belirlenir denklem
Bernoulli
 ,
,
nerede
H2
- H1
- ağırlık merkezlerinin yüksekliklerindeki fark
keyfi olarak seçilmiş bölümlerden
yatay seviye;
v1,
v2
- bölümlerdeki ortalama yağ hızları;
g - kuvvet ivmesi
yer çekimi;

hareket sırasında hidrolik kayıplar
birinci bölümden ikinciye yağlar.
denklem
Bernoulli tam kullanımda
pompaların emiş hatlarının hesaplanması için;
diğer durumlarda, ilk terim,
genellikle ihmal edilir ve dikkate alınır:

hidrolik
kayıplar genellikle yerel olarak ayrılır
uzunluk boyunca kayıplar ve sürtünme kayıpları
boru hatları (doğrusal).
1.5.1
yerel kayıplar
enerjiler yerel kaynaklıdır
hidrolik direnç,
akış bozulmasına neden olur. Yerel
dirençler şunlardır: daralmalar,
boru hatlarının genişletilmesi, yuvarlatılması,
filtreler, kontrol ekipmanları ve
düzenleme, vb. Akarken
yerel dirençler aracılığıyla sıvılar
hızı değişir ve genellikle
büyük girdaplar.
kayıplar
yerel direnişlerden gelen baskı
formül tarafından belirlenir Weisbach:
 MPa
MPa
(veya
 Pa),
Pa),
nerede

kayıp,
v
kesit üzerindeki ortalama akış hızıdır
yerel direncin arkasındaki bir boruda, m/s;
,
N/m3;
g=9.81 m/s2.
Her biri
yerel direnç karakterize edilir
katsayı değeri ile

Türbülanslı akışta, değerler
direnç ve çok az değişiklik
bölümün boyutunda bir değişiklikle, hız
Akışkan akışı ve viskozite. Böyle
sayıya bağlı olmadıklarını varsayalım
Reynolds Re.
değerler

örneğin, aynı tees için
kanal çapları eşit alınır,
Eğer:
Canlı Yayınlar
toplamak, ayrılmak; akış
geçen;









de
boru dirseği

değerler

hidrolik sistem ekipmanlarında, alınan
referans literatürü.
saat
laminer akış (Re
kayıplar
yerel direnişlerden gelen baskı
laminer akış tarafından belirlenir
formül:
 MPa
MPa
nerede

= a

Miktarları
standart basınç kaybı
için hidrolik cihazlar
nominal akış hızı genellikle
teknik özelliklerinde listelenmiştir.
1.5.2
üzerinde kayıp
uzunluk sürtünmesi
meydana gelen enerji kaybıdır
sabit kesitli düz borularda,
şunlar. üniform sıvı akışı ile,
ve uzunlukla orantılı olarak artar
borular. Bu kayıplar iç
bir sıvıda sürtünme ve bu nedenle
hem kaba hem de pürüzsüz borulara yerleştirin.
kayıplar
boru hattı sürtünme basıncı
formül tarafından belirlenir Darcy:
 MPa
MPa
nerede

ben
ve
- boru hattının uzunluğu ve iç çapı,
mm.
Bu
formül hem laminer için geçerlidir,
türbülanslı akışta olduğu gibi; fark
sadece katsayı değerlerinden oluşur

saat
laminer akış (Re
saat
türbülanslı akış sürtünme katsayısı
sadece Re'nin bir fonksiyonu değil, aynı zamanda
ayrıca iç yüzeyin pürüzlülüğüne de bağlıdır.
boru yüzeyi. İçin hidrolik olarak
düz borular,
şunlar. öyle bir sertlikle
pratik olarak direncini etkilemez,
türbülanslı sürtünme katsayısı
mod formülle belirlenebilir bilgisayar.
Konakova:

boru
hidrolik olarak pürüzsüz kabul edilir, eğer
(d/k)>(Re/20),
burada k eşdeğer pürüzlülüktür,
mm. Örneğin, yeni dikişsiz çelik için
borular k≈0.03
mm ve birkaç yıl çalıştıktan sonra
k≈0.2
mm, yeni dikişsiz borular için
demir dışı metaller k≈0,005
mm. Bu borular genellikle
takım tezgahlarının hidrolik sistemleri.
katsayı
türbülanslı rejimde sürtünme olabilir
formülle belirlemek Altşulya,
evrensel olmak (yani uygulanabilir
her halükârda):

2. Boru hattı akış modülünün akış özellikleri
Hatırlayalım
doğrusal kayıp formülü - Darcy formülü
-Weisbach:
 .
.
ifade etmek
bu formülde V hızı
akış boyunca Q
orandan
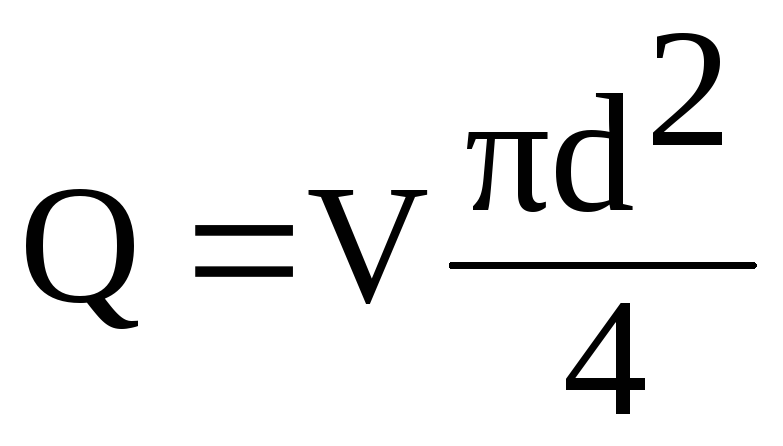
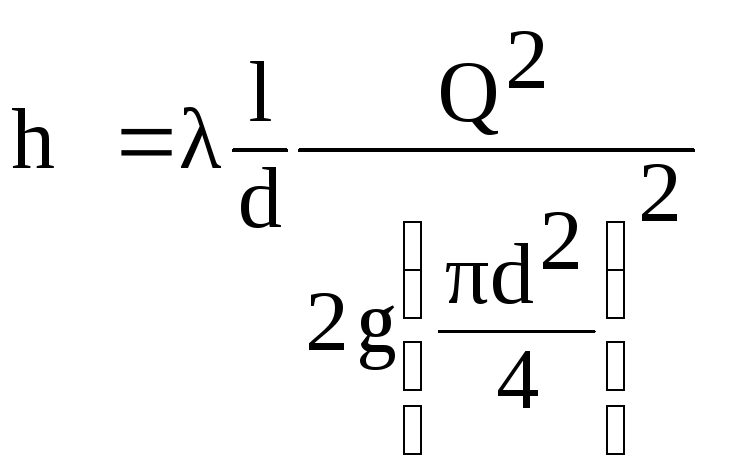
(6.1)
İçin
belirli bir çapta boru hattı
miktarlar kompleksi
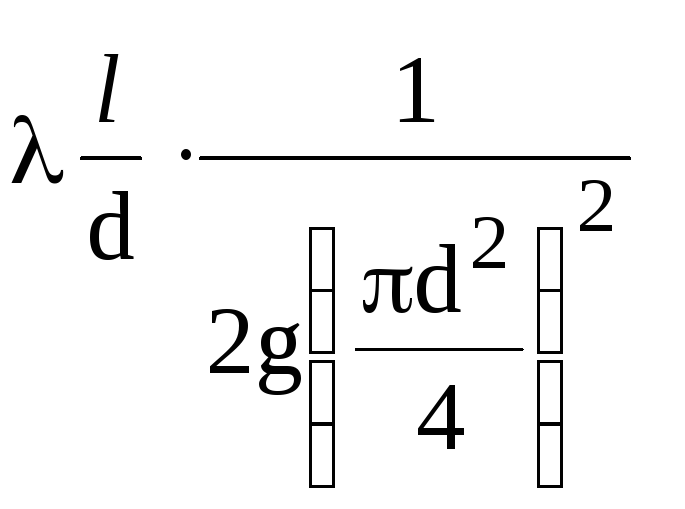
sabit (1/K2),
hidrolik katsayı hariç
sürtünme λ. Konsepte dayalı
ortalama ekonomik hız Vben
gösterilen katsayının λ olduğunu gösterelim
bu komplekse atfedilebilir, çünkü v
Bu durumda Reynolds sayısı
belirli bir anlamı var:
 ,
,
ve Nikuradze grafiğinde, λ katsayısı
bu davanın belirli bir özelliği olacak
anlam.
Savunmak
kavramı tanıtmanın meşruiyeti
ortalama ekonomik hız aşağıdaki gibidir
akıl yürütme.
hidrolik
sıhhi tesisat gibi sistem
belirli bir masrafı atlayabilirsiniz
farklı çaplarda borulardan yapılmıştır. saat
Aynı zamanda, d çapındaki bir artışla,
bu nedenle, V hızında bir azalma
sermaye harcamaları artacak ve
işletme maliyetleri
hidrolik düşüş nedeniyle azalma
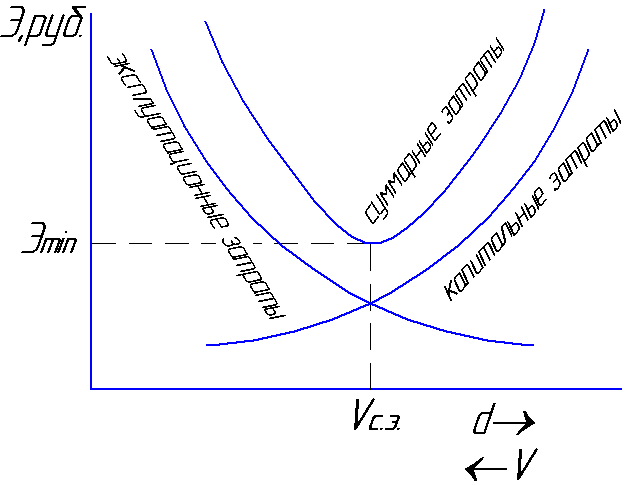
kayıplar. Toplamın hangi hızda
maliyetler minimum olacak
ortalama ekonomik olarak adlandırılacak
hız Vben
= 0.8 ... 1.3 m / s (Şekil 6.1).
şek.6.1
O zamanlar
lineer kayıp formülü (6.1) şeklini alır
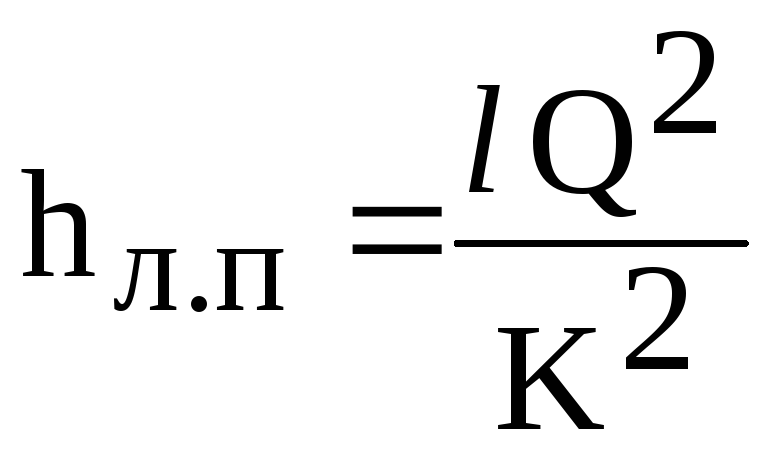
(6.2)
nerede
K - boru hattının akış özelliği
(akış modülü), malzemeye bağlı
boru hattı, çap ve akış. alınmış
tablolardan.
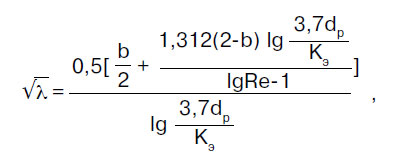
 ),C
),C ,
,