Calculation of the useful supply of thermal energy ESO PE table N P1.7

6 Calculation of economic damage associated with failures of heating networks

General economic damage,

AND_yi
= AND_y1
+and_y2
+and_bonds
,

where I_y1
— losses of thermal energy in pipelines associated with coolant leaks (lost profits), thousand rubles/year;

AND_y2
— compensation for losses to consumers of thermal energy, thousand rubles/year;

AND_bonds
— expenses for unscheduled repairs of heating network equipment, thousand rubles/year.

2.6 1 Heat losses in pipelines, thousand rubles/year

AND_y1
= Q_sweat
* C_te

where Q_sweat
— the amount of lost thermal energy associated with failures of the heating network, Gcal per year;

C_te
— price of 1 Gcal of heat supplied to the consumer, rub/Gcal;

Q_sweat.open
= q_sweati
*l _i
*n_i
* T_{feces i}

where q_sweati
— the specific number of heat energy leakages for a given failure mode of the heating system, Gcal/rm-day-unit of the failure type, is determined according to the data in Table 4;

n_i
- the number of failures of the heating network of a given nature, is determined by the results of processing statistical data;

T_{cal i}
- the time elapsed from the moment the failure was detected to its elimination, days;

l_i
- the length of the replaced section of the heating network when the failure is eliminated, running meters.

Table 2.6.1 Calculation of Q_sweat
for each failure mode

The nature of the failure	qsweat	n	Tfeces	l	Qsweat
Fistula	0,05	34	6	0,4	4,08
pipe rupture	0,279	14	5	5	97,65
Weld rupture	0,015	14	5	3	3,15
Damage to the stuffing box compensator	0,005	10	3	0,1	0,015
Valve failure	0,001	9	3	0,2	0,0054

Q_sweat
= 104.9 Gcal/year

C_te
\u003d 227.04 rubles / Gcal

AND_y1
= 227.04 * 104.9 = 23816.5 rubles / year

AND_y1
=0.0238165 million rubles/year

2.6.2 Compensation for losses to heat consumers

Compensation for losses to consumers for undersupply or reduction of coolant parameters is determined in accordance with the terms of commercial contracts between the energy supply organization and the consumer of thermal energy, million rubles / year,

AND_y2
= C_{great dane}
*Q_sweat
. _open
.

where C_{great dane}
— the contractual price of industrial damage per 1 Gcal of unsupplied heat energy, thousand rubles/Gcal.

C_{great dane}
= 227.64 rubles / year

AND_y2
= AND_y1
=0.0238165 million rubles/year

2.6.3 Costs for unscheduled equipment repairs

This item includes the costs of detecting a leak, earthworks, direct repairs (installation of patches, welding, etc.) and does not include the cost of construction and installation work related to the replacement of heating network equipment.

AND_bonds
= EC_{rem i}
*n _i
*l _i

Where is C _{rem i}
— specific cost of repair work to eliminate water leaks in heating networks with a given failure mode, thousand rubles/linear meter;

n_i
- the number of failures of the heating network of a given nature;

l_i
- the length of the replaced section of the heating system, running meters.

Table 2.6.3 Calculation of AND_bonds
for each failure mode

The nature of the failure	n	l	C rem	ANDbonds
Fistula	34	0,5	0,9	15,3
pipe rupture	14	4	0,5	28
Weld rupture	14	3	0,5	21
Damage to the stuffing box compensator	10	0,3	0,5	1,5
Valve failure	9	0,3	0,5	1,35

AND_bonds
= 67.15 thousand rubles / year

AND_yi
=0.0238165 + 0.0238165 + 0.06715= 0.114783 million rubles/year

General operating costs, thousand rubles / year,

AND_{the ex}
= AND_sign
+and_lane
+and_sn
+and_am
+and_rem
+and_yi

AND_{the ex}
= 5.85 +10.95679013 + 5.321122 + 3.332 + 7.981683 + 0.114783 = 33.556378 million rubles/year

Disclosure obligation

According to Decree of the Government of the Russian Federation No. 570 dated July 5, 2013, heat supply organizations are required to disclose information about their activities on the Committee's website in the form of UIAS templates. To do this, it is necessary to download and send the completed templates in the EIAS system within the following terms:

one-time (or within 10 days from the date of changes) - information about the organization (JKH.OPEN.INFO.ORG);

within 10 days from the date of filing an application for setting tariffs (JKH.OPEN.INFO.REQUEST);

within 30 calendar days from the date of adoption of the order on setting tariffs (JKH.OPEN.INFO.PRICE);

within 30 calendar days from the date of submission of the balance sheet to the Federal Tax Service, but no later than April 30 (for organizations that do not submit the annual balance sheet to the tax authorities (JKH.OPEN.INFO.BALANCE);

within 30 calendar days after the end of the quarter (except for MSW operators) (JKH.OPEN.INFO.QUARTER).

If there have been changes in the disclosed information, information about these changes shall be published in the same sources in which the relevant information was originally published within 10 calendar days from the date of the information change.

In addition, heat supply organizations, as part of the disclosure of information, are obliged to publish the following information on their official website on the Internet:

- Until March 1 annually - On the conditions under which the supply of goods (rendering of services), as well as information on contracts concluded in accordance with Parts 2.1 and 2.2 of Article 8 of the Federal Law "On Heat Supply";

— Quarterly, before the 10th day of the month following the reporting quarter — On the decommissioning of thermal energy sources, heating networks; On the grounds for suspension, restriction and termination of the mode of consumption of thermal energy in the cases provided for in paragraphs 70 and 76 of the Rules for organizing heat supply in the Russian Federation.

Full information about the information disclosure standards and the procedure for their implementation is available on the Committee's website in the "Other Information" section - the "Information Disclosure" subsection (or the "Information Disclosure" banner).

Regulation 2018 in the field of heat supply

Information Letter of the Tariff Regulation Committee of the Volgograd Region dated March 23, 2017 No. 31-06-08/643
Sample statement on the choice of the method of regulation Sample statement on the adjustment Sample statement on the establishment of tariffs Reports on the results of work on the regulated type of activityList of documents for correcting long-term Calculation of tariffs for heat energy Calculation tables when choosing an indexation method

Instructions for filling out economic justification forms Long-term tariff Economic justification

transcript

1

2 Calculation of useful supply of heat carrier Appendix 4.2 p.p. Indicators (thousand m³) Period (plan for 2015) including total water steam Heat carrier production, total, 690, .465 25.124 including: -CHP 25 MW and more CHP less than 25 MW. 690, .465 25.124 — boiler electric boilers Purchased heat carrier Consumption of heat carrier for household needs. 2.212 2, Coolant supply to the network (clause 1+clause 2-clause 3). 688, ,253 25, Regulatory losses in the transfer of coolant. 170, , Volume of returned coolant Useful supply of coolant to consumers (p.4 - p.5.-p.6). 518, .892 25.124

3 Annex 5.2 Calculation of operating (controllable) costs for each year of the long-term period for water coolant Parameters for calculating costs Unit of measurement Long-term period Consumer price index for the billing period (CPI) 1.047 1.047 assets (IAC) the number of conventional units related to c.u. 1443, , ,113 to assets required for activities 3.2 installed thermal capacity of a heat source 4 Cost elasticity coefficient for asset growth (K el ) 5 Operating (controlled) Gcal/h thousand rubles

4 Appendix 5.2 Calculation of operating (controllable) costs for each year of the long-term period for steam coolant Cost calculation parameters Unit of measurement Long-term period Consumer price index for the billing period (CPI) 1.047 1.047 assets (IAC) the number of conventional units related to c.u. 1443, , ,113 to assets required for activities 3.2 installed thermal capacity of a heat source 4 Cost elasticity coefficient for asset growth (K el ) 5 Operating (controlled) Gcal/h thousand rubles

5 Appendix 5.9 Calculation of the required gross revenue by indexing the established tariffs for water coolant Expense year i0 to year i0 + 1 to year i1 to n 1 Operating (controlled) Uncontrolled Costs for the acquisition (production) of energy resources,cold water and heat carrier 4 Profit 5 Results of activities before the transition to price (tariff) regulation based on long-term parameters 6 Adjustment to take into account the deviation of the actual values ​​of tariff calculation parameters from the values ​​taken into account when setting tariffs 7 Adjustment taking into account the reliability and quality of goods sold (services rendered), subject to accounting in the RGR 8 Adjustment of the RGR in connection with a change (non-fulfillment) of the investment program 9 Adjustment subject to accounting in the RGR and taking into account the deviation of the actual indicators of energy saving and energy efficiency increase from the established planned (calculated) indicators and the deviation of the terms of the program implementation in the field of energy saving and energy efficiency improvement from the established deadlines for the implementation of such a program 10 TOTAL required gross revenue 11 Commodity revenue

6 Appendix 5.9 Calculation of the required gross revenue by indexing the established tariffs for the heat carrier steam Name of consumption year i0 to year i0 + 1 to year i1 to n 1 Operating (controlled) Non-controlled Performance results before the transition to price (tariff) regulation based on long-term parameters 6 Adjustment to take into account the deviation of the actual values ​​of tariff calculation parameters from the values ​​taken into account when setting tariffs 7 Adjustment taking into account the reliability and quality of goods sold (rendered services), subject to accounting in the NGR 8 Adjustment of the NRV in connection with the change (failure) of the investment program 10 TOTAL required gross revenue 11 Commodity revenue

2 We calculate the annual payroll fund for two additionally hired operators in connection with the expansion of the boiler house

№	Name indicator	unit of measurement	Value
1	Worker Fund time	Hour	1986
2	Medium rank		5
3	Average tariff bid	rub./hour	45
4	Quantity workers	people	2
5	Number of people hour worked at the rate	people hour	3972
6	Number of people hours worked per night	people hour	1324
7	Quantity holiday people. hour	people hour	87,384
8	Number of people hour for processing	people hour	130
9	payroll fund tariff fees	rub.	178740
10	Award for implementation of a plan	rub.	71496
11	Additional pay for work at night	rub.	23832
12	Additional pay for work on holidays	rub.	1966,14
13	Surcharge for processing	rub.	2925
14	Total core wages	rub.	278959,14
15	Additional wage	rub.	27895,914
16	annual fund wages	rub.	306855,054
17	annual fund wages, taking into account the district coefficient	rub.	352883,312
18	Average monthly one worker's wages	rub.	14703,47
Expenses to pay basic wages Szp = 352883,312 rub./year

7.
Deductions for social needs, rub./year.

Sn =
Szp ·
Tsv, rub./year

Szp - costs for
payment
basic salary,
rub./year;

Tsv - Tariff
insurance rates, %

№	Names deductions	unit of measurement	Value
1	Deductions in the Pension Fund at a rate of 22%	rub.	77634,32
2	Deductions in the FSS at a rate of 2.9%	rub.	10233,61
3	Deductions in FFOMS at a rate of 5.1%	rub.	17997,04
4	Deductions in the Federal Social Security Service at a rate of 0.2%	rub.	705,76
	Total:	rub.	106570,73

8.
Costs
maintenance and operation of equipment,
rub./year:

We accept the standard
for this article 10% of the purchase price
equipment

rub./year

9.
Depreciation deductions, rub./year

(According to
regulation on accounting "Accounting
fixed assets" PBU
6/01)

№	Name fixed assets	Estimated period	Notes
initial cost, thousand rubles	norm depreciation charges, %	Sum depreciation charges, thousand rubles
1	2	3	4	5	6
1	Hot water boiler KVGM-10-150	2480	10	248	OKOF code 14 2897030
	Total:	2480	10	248

10.
Property tax expenses

,
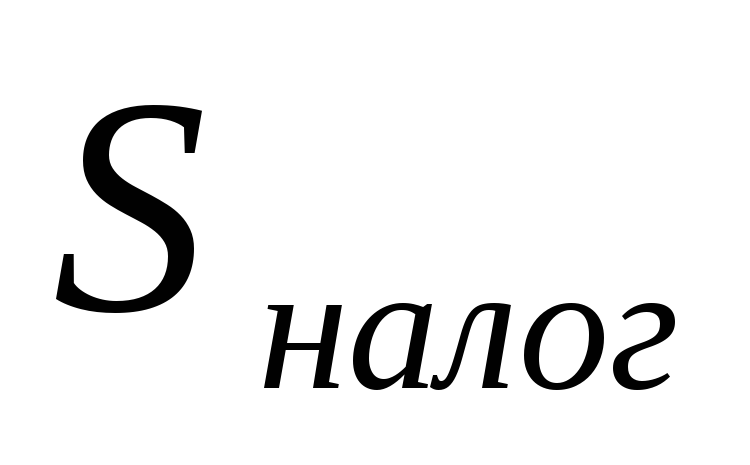
rub./year:

Property tax
is 2.2% of the cost of equipment

rub./year

10.
Expenses for other needs

,
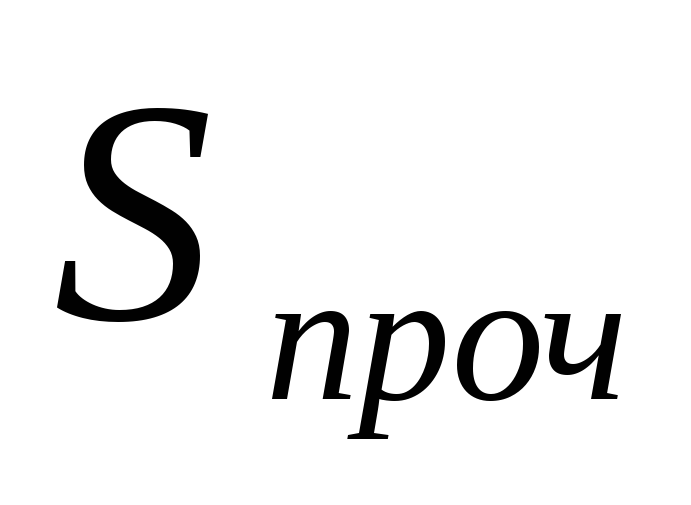
rub./year:

This
item includes expenses not included
in other items (including costs
for repairs and maintenance).

,
rub./year,

thousand
rub./year

11.
Full cost of annual volume
thermal energy production,
thousand rubles/year:

,
rub./year

№	Articles costs	Designation	Sum, thousand rubles/year
1	Expenses for materials	Sm	45,9
2	Expenses for fuel	ST	9685,36
3	Expenses for electricity	Se	1038,28
4	Expenses on the water	Sv	242,21
5	Salary staff pay	Szp	352,88
6	Deductions for social needs	Sw	106,57
7	depreciation deductions	Sam	248
8	RSEO	Srseo	248
9	Expenses to pay property tax	Stax	54,56
10	Other expenses	Spr	1202,17

12.
Total unit cost of production
thermal energy, rub./year:

,
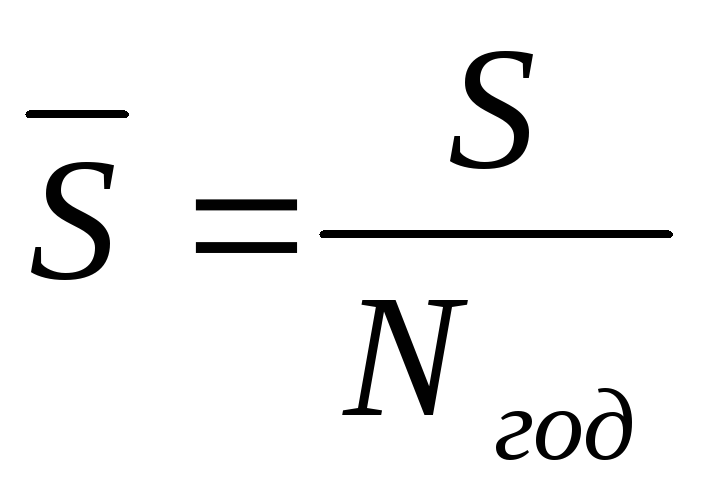
RUB/GJ,

where

GJ/year
– total annual heat supply
consumers.

RUB/GJ, (481.81
RUB/Gcal)

To determine the main development trend, the values ​​of empirical levels are depicted on the graph y f t.

The change in the number of failures of heat networks for the proposed period of time, depending on the nature of the failure, is taken as a dynamic series. Empirical levels of the series are smoothed by the moving average method. The smoothed levels are plotted on the chart.

Failure Mode - Pipe Burst

Failure Mode - Weld Break

Failure mode - Damage to the stuffing box compensator

Failure mode - valve failure

1.2 DERIVATION OF THE TREND EQUATION

The graphic representation of the smoothed levels clearly shows the main trend in the number of failures of heat networks for various reasons.

The next stage of work is to obtain a generalized statistical assessment of the trend by the method of analytical alignment.

The main development trend y_t
as a function of time:

y_ti
= f(t_i
).

Determination of theoretical (calculated) levels y_ti
is produced on the basis of an adequate mathematical model, which most accurately reflects the main trend of the dynamics series - the number of heating system failures for this reason.

The selection of a mathematical function is based on determining the type of development of an economic phenomenon in time.

When the trend type is set, it is necessary to calculate the optimal values ​​of the trend parameters based on the actual levels, i.e. get the values ​​of the coefficients of the equation. Based on the requirements of the least squares method (LSM), a system of normal equations is compiled, solving which, we calculate the trend parameters.

For a linear trend, the normal MKT equations have the form:

n*a + b*St _i
= Sy _i

a*St _i
+ b*St2_i
= S y_i
*t_i

where y_i
are the levels of the initial series of dynamics;

t_i
– numbers of periods or moments of time;

Normal MKT equations for a trend in the form of a 2nd order parabola:

n*a + b*St_i
+ c*St_i2
= Sy_i

a*St_i
+ b*St_i2
+ c*St_i3
= Sy_i
*t_i

a*St_i2
+ b*St_i3
+ c*St_i4
= Sy_i
*t_i2

where y_i
– levels of a series of dynamics;

t_i
– numbers of periods or moments of time;

a, b, c are the constants of the equations.

Table 1.2.1 Formation of data for the derivation of the trend equation - the nature of the failure of the fistula

fistula	Yi	moving average (3 years)	Ti	Yi*Ti	Ti*Ti	Yi*Ti 2	Ti 3	Ti 4	Ti 2
1991	25	—	1	25	1	25	1	1	1
1992	31	30,33333333	2	62	4	124	8	16	4
1993	35	31,66666667	3	105	9	315	27	81	9
1994	29	31,66666667	4	116	16	464	64	256	16
1995	31	30	5	155	25	775	125	625	25
1996	30	32,66666667	6	180	36	1080	216	1296	36
1997	37	33,33333333	7	259	49	1813	343	2401	49
1998	33	34,33333333	8	264	64	2112	512	4096	64
1999	33	33,66666667	9	297	81	2673	729	6561	81
2000	35	—	10	350	100	3500	1000	10000	100
total	319	257,6666667	55	1813	385	12881	3025	25333	385

For a linear trend:

10*a +55*b = 319; a = 28;

55*a + 385*b = 1813; b = 0.71;

y \u003d 28 + 0.71 * t;

For a trend in the form of a second-order parabola:

10*a + 55*b + 385*c = 319; a = 26.02;

55*a + 385*b + 3025*c = 1813; b = 1.7;

385*a + 3025*b + 25333*c = 12881; c = -0.09;

y = 26.02 + 1.7*t -0.09*t2
;

pipe rupture	Yi	slip cf. for 3 years	Ti	Yi*Ti	Ti*Ti	Yi*Ti 2	Ti 3	Ti 4	Ti 2
1991	12	1	12	1	12	1	1	1
1992	8	10	2	16	4	32	8	16	4
1993	10	9,666667	3	30	9	90	27	81	9
1994	11	11,33333	4	44	16	176	64	256	16
1995	13	11,33333	5	65	25	325	125	625	25
1996	10	11,66667	6	60	36	360	216	1296	36
1997	12	11,33333	7	84	49	588	343	2401	49
1998	12	13	8	96	64	768	512	4096	64
1999	15	12,66667	9	135	81	1215	729	6561	81
2000	11	10	110	100	1100	1000	10000	100
total	114	91	55	652	385	4666	3025	25333	385

For a linear trend:

y \u003d 9.75 + 0.3 * t;

For a trend in the form of a second-order parabola:

y = 9.82 + 0.26*t + 0.004*t2
;

Table 1.2.3 Formation of data for the derivation of the trend equation - the nature of the failure weld rupture.

seam rupture	Yi	cf. rolling for 3 years	Ti	Yi*Ti	Ti*Ti	Yi*Ti 2	Ti 3	Ti 4	Ti 2
1991	10	1	10	1	10	1	1	1
1992	6	7,666667	2	12	4	24	8	16	4
1993	7	6,666667	3	21	9	63	27	81	9
1994	7	8,333333	4	28	16	112	64	256	16
1995	11	9	5	55	25	275	125	625	25
1996	9	10,33333	6	54	36	324	216	1296	36
1997	11	11,66667	7	77	49	539	343	2401	49
1998	15	12	8	120	64	960	512	4096	64
1999	10	12,33333	9	90	81	810	729	6561	81
2000	12	10	120	100	1200	1000	10000	100
total	98	78	55	587	385	4317	3025	25333	385

For a linear trend:

y \u003d 6.61 + 0.58 * t;

For a trend in the form of a second-order parabola:

y = 7.27+ 0.25*t + 0.03*t2
;

S/c	Yi	avg moving for 3 years	Ti	Yi*Ti	Ti*Ti	Yi*Ti 2	Ti 3	Ti 4	Ti 2
1991	7	1	7	1	7	1	1	1
1992	12	9,666667	2	24	4	48	8	16	4
1993	10	11	3	30	9	90	27	81	9
1994	11	12	4	44	16	176	64	256	16
1995	15	12,66667	5	75	25	375	125	625	25
1996	12	13	6	72	36	432	216	1296	36
1997	12	10,33333	7	84	49	588	343	2401	49
1998	7	9,666667	8	56	64	448	512	4096	64
1999	10	10	9	90	81	810	729	6561	81
2000	13	10	130	100	1300	1000	10000	100
total	109	88,33333	55	612	385	4274	3025	25333	385

y = 9.69 + 0.22*t;

For a trend in the form of a second-order parabola:

y \u003d 7.66 + 1.36 * t - 0.11 * t2
;