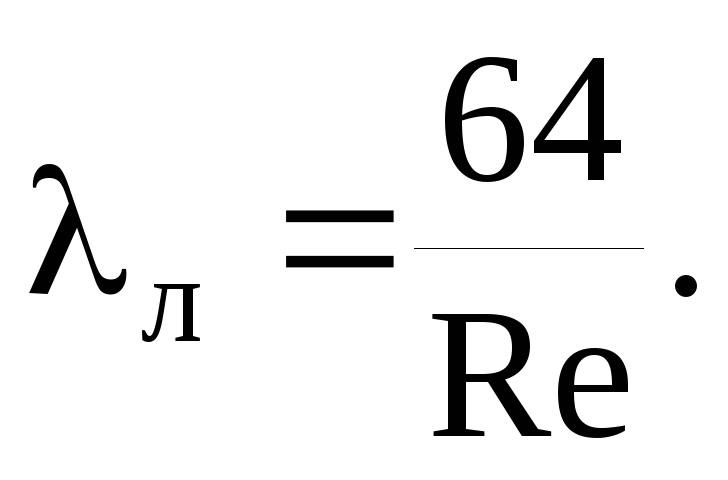1. Hidrostatički tlak
Hidrostatički tlak je
unutarnja tlačna sila zbog
djelovanjem vanjskih sila primijenjenih na
zadana točka u tekućini. Takav pritisak
u svim smjerovima je isti i ovisi
o položaju točke u tekućini koja miruje.
Dimenzija hidrostatskog tlaka
u sustavu MKGSS - kg / cm2 ili t / m2,
u SI sustavu - N/m2.
Omjeri osnovnih jedinica
pritisak:
|
kg/cm2 |
N/m2 |
|
|
tehnička atmosfera |
1 |
98066,5 |
|
milimetar vodenog stupca |
0,0001 |
9,80665 |
|
milimetar žive |
0,00136 |
133,32 |
U praktičnim proračunima, 1 tehnički
atmosfera \u003d 1 kg / cm2 \u003d 10 m vode. Umjetnost. =
735 mmHg Umjetnost. = 98070 N/m2.
Za nestlačivu tekućinu koja je
u ravnoteži pod snagom
gravitacijski, potpuno hidrostatski
točkasti pritisak:
p=p+

gdje je p pritisak na slobodnu
površina tekućine;

visina h s površinom
presjek jednak jedan;
h - dubina uranjanja
bodovi;

Za neke tekućine, vrijednosti
specifična težina korištena u rješavanju
zadaci su dati u dodatku (tab.
P-3).
Vrijednost viška tlaka preko
atmosferski (stra)
naziva se manometrijskim, ili
nadtlak:

Ako je pritisak na slobodnu površinu
jednak atmosferskom, zatim višak
pritisak strm=

Pod atmosferskim tlakom
količina se zove vakuum:
Rotkačiti= stra- R.
Rješenje za većinu problema ovog
dio se odnosi na uporabu
osnovna jednadžba hidrostatike

gdje je z koordinata ili
oznaka točke.
1. Opći podaci o hidrauličkom proračunu cjevovoda
Prilikom izračunavanja
cjevovodi koji se razmatraju
stabilan, ujednačen pritisak
kretanje bilo koje tekućine
turbulentni režim, u okruglo-cilindričnom
cijevi. Tekućina u tlačnim cijevima
je pod pritiskom i
presjeci su im potpuno
ispunjena. Kretanje tekućine uzduž
kao rezultat toga nastaje cjevovod
činjenica da je pritisak na početku toga veći od
na kraju.
Hidraulični
izračun se radi kako bi se utvrdilo
promjer cjevovoda d
s poznatim
duljina kako bi se osiguralo preskakanje
određeni protok P
ili uspostavljanje
kod zadanog promjera i duljine potrebne
tlaka i protoka tekućine. Cjevovodi
ovisno o duljini i uzorku njihova
mjesta se dijele na jednostavne
i složena. Za jednostavne cjevovode
uključuje cjevovode koji nemaju
grane po dužini, s konstantom
isti trošak.
Cjevovodi
sastoje se od cijevi istog promjera
cijelom dužinom ili iz dijelova cijevi različitih
promjera i duljina. Zadnji slučaj
odnosi se na serijsku vezu.
Jednostavni cjevovodi
ovisno o duljini s parcelom mjesnog
otpori se dijele na kratke i
dugo. kratak
cjevovodi
su
cjevovodi dovoljno kratke duljine,
u kojem lokalni otpor
čine više od 10% hidrauličkih
gubitak dužine. Na primjer, oni uključuju:
sifonske cijevi, usisne
cijevi krilnih pumpi, sifona (tlačni
vodovodne cijevi ispod nasipa ceste),
cjevovodi unutar zgrada i građevina
itd.
dugo
cjevovodi
pozvao
cjevovodi su relativno veliki
duljine u kojima je gubitak glave po dužini
znatno nadmašuju lokalne
gubici. Lokalni gubici su
manje od 5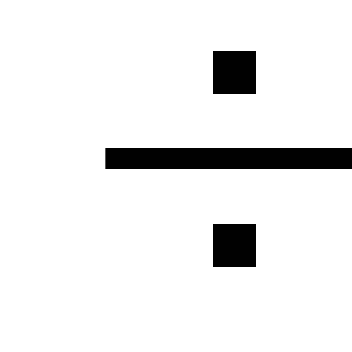
gubici duž duljine cjevovoda, a samim tim
mogu se zanemariti ili uvesti kod
povećavaju se hidraulički proračuni
koeficijent jednak 1,05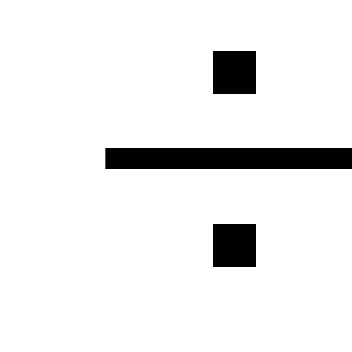
Dugi cjevovodi ulaze u sustav
vodovodne mreže, crpni kanali
stanice, kanali i cjevovodi
industrijska poduzeća i
poljoprivredne namjene i
itd.
Složeni cjevovodi
imaju različite grane po dužini,
oni. cjevovod se sastoji od mreže cijevi
određenim promjerima i duljinama. Kompleks
cjevovodi se dijele na
paralelna, slijepa ulica (razgranat),
prstenasti (zatvoreni) cjevovodi,
uključeni u vodovodnu mrežu.
Hidraulični
proračun cjevovoda se smanjuje kao
obično za rješavanje tri glavna problema:
-
definicija
protok cjevovoda P,
ako je poznato
pritisak H,
duljina l
i promjera d
cjevovod,
s obzirom na dostupnost određenih lokalnih
otpori ili u njihovoj odsutnosti; -
definicija
potreban pritisak H,
potrebno za osiguranje propusnice
poznati tok P
cjevovodom
duljina l
i promjera d; -
definicija
promjer cjevovoda d
kada
poznate vrijednosti glave H,
trošak P
i duljina l.
Brzina protoka tekućine je
gdje je q > projektni protok tekućine, m3/s;
- površina živog dijela cijevi, m2.
Koeficijent otpora trenja λ utvrđuje se u skladu s propisima skupa pravila SP 40-102-2000 „Projektiranje i montaža cjevovoda za vodoopskrbne i kanalizacijske sustave od polimernih materijala. Opći zahtjevi":
gdje je b neki broj sličnosti režima strujanja fluida; za b > 2 uzima se b = 2.
gdje je Re stvarni Reynoldsov broj.
gdje je ν koeficijent kinematičke viskoznosti tekućine, m²/s. Prilikom izračunavanja cijevi za hladnu vodu, uzima se jednako 1,31 10-6 m² / s - viskoznost vode na temperaturi od +10 ° C;
Rekv > - Reynoldsov broj koji odgovara početku kvadratne regije hidrauličkog otpora.
gdje je Ke hidraulička hrapavost materijala cijevi, m. Za cijevi od polimernih materijala uzima se Ke = 0,00002 m ako proizvođač cijevi ne daje druge vrijednosti hrapavosti.
U onim slučajevima protoka kada je Re ≥ Rekv, izračunata vrijednost parametra b postaje jednaka 2, a formula (4) se značajno pojednostavljuje, pretvarajući se u dobro poznatu Prandtlovu formulu:
Kod Ke = 0,00002 m, kvadratna regija otpora javlja se pri protoku vode (ν = 1,31 10-6 m²/s) jednakoj 32,75 m/s, što je praktički nedostižno u javnim vodoopskrbnim sustavima.
Za svakodnevne proračune preporučuju se nomogrami, a za točnije izračune - "Tablice za hidraulične proračune cjevovoda od polimernih materijala", svezak 1 "Tlačni cjevovodi" (A.Ya. Dobromyslov, M., VNIIMP, 2004).
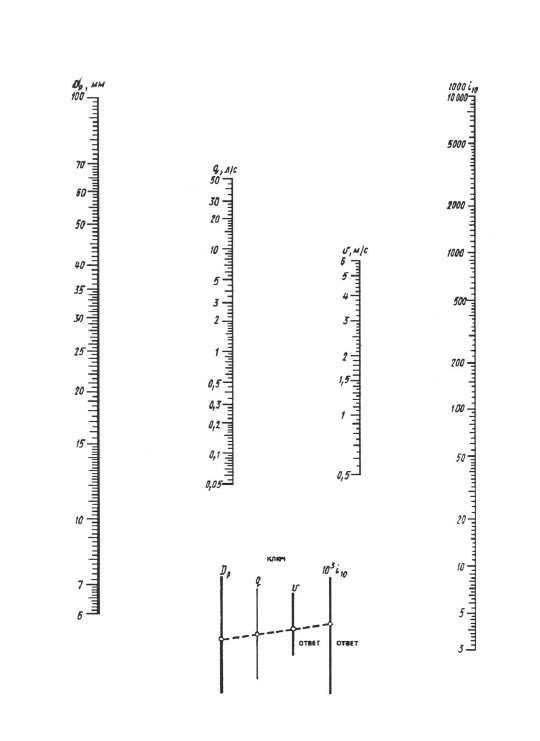
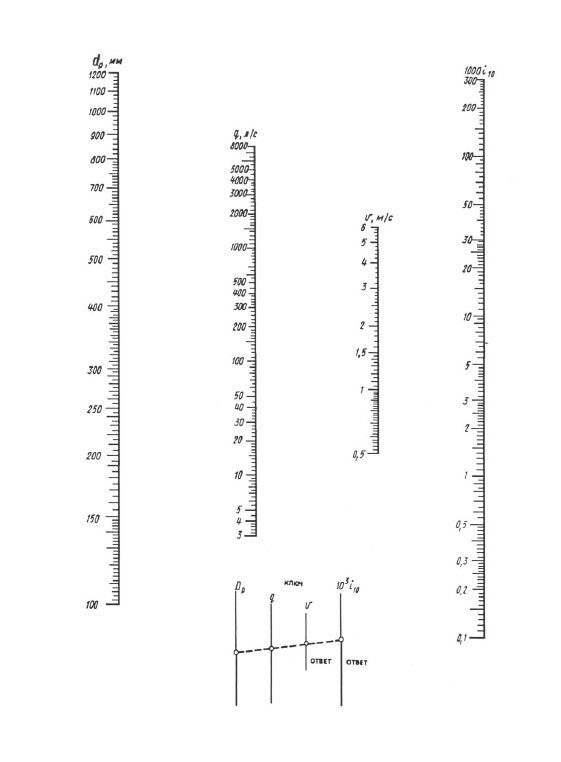
Prilikom izračuna prema nomogramima, rezultat se postiže jednim prekrivanjem ravnala - trebate povezati točku s vrijednošću izračunatog promjera na dp skali s točkom s vrijednošću izračunate brzine protoka na q (l / s) skala s ravnom linijom, ovu ravnu liniju nastaviti sve dok se ne siječe s ljestvicama brzine V i specifičnih gubitaka glave 1000 i (mm/m). Točke sjecišta ravne linije s ovim mjerilima daju vrijednost V i 1000 i.
Kao što znate, trošak električne energije za crpljenje tekućine izravno je proporcionalan vrijednosti H (ceteris paribus). Zamijenivši izraz (3) u formulu (2), lako je vidjeti da je vrijednost i (i, posljedično, H) obrnuto proporcionalna izračunatom promjeru dp do petog stupnja.
Gore je prikazano da vrijednost dp ovisi o debljini stijenke cijevi e: što je stijenka tanja, to je veći dp i, sukladno tome, manji je gubitak tlaka zbog trenja i trošak električne energije.
Ako se vrijednost MRS cijevi iz bilo kojeg razloga promijeni, njezin promjer i debljina stijenke (SDR) moraju se ponovno izračunati.
Treba imati na umu da u nizu slučajeva korištenje cijevi s MRS 10 umjesto cijevi s MRS 8, posebno cijevi s MRS 6.3, omogućuje smanjenje promjera cjevovoda za jednu veličinu. Stoga, u naše vrijeme, upotreba polietilena PE 80 (MRS 8) i PE 100 (MRS 10) umjesto polietilena PE 63 (MRS 6.3) za proizvodnju cijevi omogućuje ne samo smanjenje debljine stijenke cijevi, već i njihovu težinu i potrošnju materijala, ali i za smanjenje troškova energije za crpljenje tekućine (ceteris paribus).
Posljednjih godina (nakon 2013.) cijevi od polietilena PE80 gotovo su potpuno izmijenjene iz proizvodnje cijevima od polietilena razreda PE100. To se objašnjava činjenicom da se sirovine od kojih se izrađuju cijevi isporučuju iz inozemstva s markom PE100.A također i činjenica da polietilen 100 razreda ima više karakteristika čvrstoće, zbog čega se cijevi proizvode s istim karakteristikama kao cijevi od PE80, ali s tanjom stijenkom, čime se povećava propusnost polietilenskih cjevovoda.
Nomogram za određivanje gubitaka tlaka u cijevima promjera 6 100 mm.
Nomogram za određivanje gubitaka tlaka u cijevima promjera 100, 1200 mm.
Reynoldsov kriterij
Ovu ovisnost iznio je engleski fizičar i inženjer Osborne Reynolds (1842-1912).
Kriterij koji pomaže odgovoriti na pitanje postoji li potreba za razmatranjem viskoznosti je Reynoldsov broj Re. Jednaka je omjeru energije gibanja elementa tekućine koja teče i rada sila unutarnjeg trenja.
Razmotrimo element kubične tekućine s duljinom ruba n. Kinetička energija elementa je:
Prema Newtonovom zakonu, sila trenja koja djeluje na fluidni element definira se na sljedeći način:
Rad ove sile pri pomicanju fluidnog elementa na udaljenosti n je
a omjer kinetičke energije fluidnog elementa i rada sile trenja je
Smanjujemo i dobivamo:
Re se zove Reynoldsov broj.
Dakle, Re je bezdimenzionalna veličina koja karakterizira relativnu ulogu viskoznih sila.
Na primjer, ako su dimenzije tijela s kojim je tekućina ili plin u kontaktu vrlo male, tada će čak i uz nisku viskoznost Re biti beznačajan, a sile trenja imaju prevladavajuću ulogu. Naprotiv, ako su dimenzije tijela i brzina velike, tada Re >> 1, pa čak i velika viskoznost neće imati gotovo nikakav utjecaj na prirodu gibanja.
Međutim, ne uvijek veliki Reynoldsovi brojevi znače da viskoznost ne igra nikakvu ulogu. Dakle, kada se postigne vrlo velika (nekoliko desetaka ili stotina tisuća) vrijednost Re broja, glatko laminarno (od latinskog lamina - "ploča") tok prelazi u turbulentno (od latinskog turbulentus - "olujan" , “kaotično”), popraćeno kaotičnim, nestalnim pokretima tekućine. Taj se učinak može primijetiti ako postupno otvorite slavinu za vodu: tanki mlaz obično teče glatko, ali s povećanjem brzine vode, glatkoća protoka je poremećena. U mlazu koji istječe pod visokim tlakom, čestice tekućine kreću se nasumično, osciliraju, svo kretanje je popraćeno snažnim miješanjem.
Pojava turbulencije uvelike povećava otpor. U cjevovodu je brzina turbulentnog strujanja manja od brzine laminarnog strujanja pri istim padovima tlaka. Ali turbulencija nije uvijek loša. Zbog činjenice da je miješanje tijekom turbulencije vrlo značajno, prijenos topline - hlađenje ili zagrijavanje agregata - događa se mnogo intenzivnije; širenje kemijskih reakcija je brže.
Bernoullijeva jednadžba stacionarnog gibanja
Jednu od najvažnijih jednadžbi hidromehanike dobio je 1738. švicarski znanstvenik Daniel Bernoulli (1700-1782). Prvi je uspio opisati gibanje idealne tekućine, izraženo u Bernoullijevoj formuli.
Idealna tekućina je tekućina u kojoj ne postoje sile trenja između elemenata idealne tekućine, kao ni između idealne tekućine i stijenki posude.
Jednadžba stacionarnog gibanja koja nosi njegovo ime je:
gdje je P tlak tekućine, ρ je njezina gustoća, v je brzina kretanja, g je akceleracija slobodnog pada, h je visina na kojoj se nalazi element tekućine.
Značenje Bernoullijeve jednadžbe je da je unutar sustava ispunjenog tekućinom (presjek cjevovoda) ukupna energija svake točke uvijek nepromijenjena.
Bernoullijeva jednadžba ima tri člana:
- ρ⋅v2/2 - dinamički tlak - kinetička energija po jedinici volumena pogonske tekućine;
- ρ⋅g⋅h - težinski tlak - potencijalna energija po jedinici volumena tekućine;
- P - statički tlak, po svom nastanku je rad tlačnih sila i ne predstavlja rezervu neke posebne vrste energije („energija tlaka“).
Ova jednadžba objašnjava zašto se u uskim dijelovima cijevi povećava brzina protoka, a smanjuje se pritisak na stijenke cijevi. Maksimalni tlak u cijevima se postavlja upravo na mjestu gdje cijev ima najveći presjek. Uski dijelovi cijevi su u tom pogledu sigurni, ali tlak u njima može pasti toliko da tekućina proključa, što može dovesti do kavitacije i uništenja materijala cijevi.
Navier-Stokesova jednadžba za viskozne tekućine
U rigoroznijoj formulaciji, linearna ovisnost viskoznog trenja o promjeni brzine tekućine naziva se Navier-Stokesova jednadžba. Uzima u obzir stišljivost tekućina i plinova i, za razliku od Newtonovog zakona, vrijedi ne samo blizu površine čvrstog tijela, već i u svakoj točki tekućine (blizu površine čvrstog tijela u slučaju nestlačivog tijela). tekućina, Navier-Stokesova jednadžba i Newtonov zakon se podudaraju).
Svi plinovi za koje je zadovoljen uvjet kontinuiranog medija također podliježu Navier-Stokesovoj jednadžbi, t.j. su Newtonove tekućine.
Viskoznost tekućina i plinova obično je značajna pri relativno malim brzinama, pa se ponekad kaže da je Eulerova hidrodinamika poseban (granični) slučaj velikih brzina Navier-Stokesove hidrodinamike.
Pri malim brzinama, u skladu s Newtonovim zakonom viskoznog trenja, sila otpora tijela proporcionalna je brzini. Pri velikim brzinama, kada viskoznost prestane igrati značajnu ulogu, otpor tijela je proporcionalan kvadratu brzine (što je prvi otkrio i potkrijepio Newton).
Slijed hidrauličkog proračuna
1.
Odabrana je glavna cirkulacija
prstenasti sustav grijanja (većina
nepovoljan položaj u hidrauličnom
odnos). U slijepoj ulici s dvije cijevi
sustavi je prsten koji prolazi kroz njega
donji instrument najudaljenijeg i
opterećen uspon, u jednocijevnom -
kroz najudaljenije i napunjene
uspona.
Na primjer,
u dvocijevnom sustavu grijanja s
gornje ožičenje glavna cirkulacija
prsten će proći od toplinske točke
kroz glavni uspon, dovodni vod,
kroz najudaljeniji uspon, grijanje
uređaj u prizemlju, povratni vod
do mjesta grijanja.
V
sustavi s povezanim kretanjem vode u
prsten se uzima kao glavni,
prolazeći kroz sredinu većinu
napunjen stalak.
2.
Pukao je glavni cirkulacijski prsten
u zaplete (zaplet je karakteriziran
konstantan protok vode i isto
promjer). Dijagram pokazuje
brojevi sekcija, njihove duljine i toplinske
opterećenja. Toplinsko opterećenje glavnog
parcele se određuju zbrajanjem
toplinska opterećenja kojima ovi služe
parcele. Za odabir promjera cijevi
koriste se dvije količine:
a)
dati protok vode;
b)
približne specifične gubitke tlaka
za trenje u projektnoj cirkulaciji
prsten Roženiti se.
Za
izračun Rk.č
treba znati duljinu glavnog
cirkulacijski prsten i izračunati
cirkulacijski tlak.
3.
Izračunata cirkulacija
formula tlaka
 ,
,
(5.1)
gdje
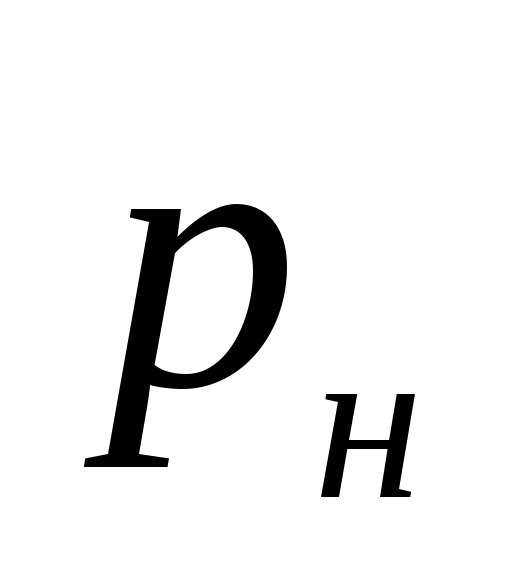
tlak koji stvara pumpa, Pa.
Praksa projektiranja sustava
grijanje je pokazalo da je najviše
preporučljivo je izmjeriti tlak pumpe,
jednak
 ,
,
(5.2)
gdje
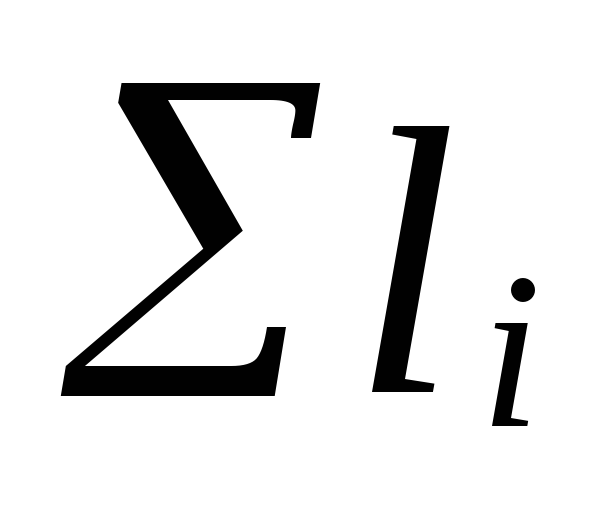
zbroj duljina presjeka glavne cirkulacije
prstenovi;
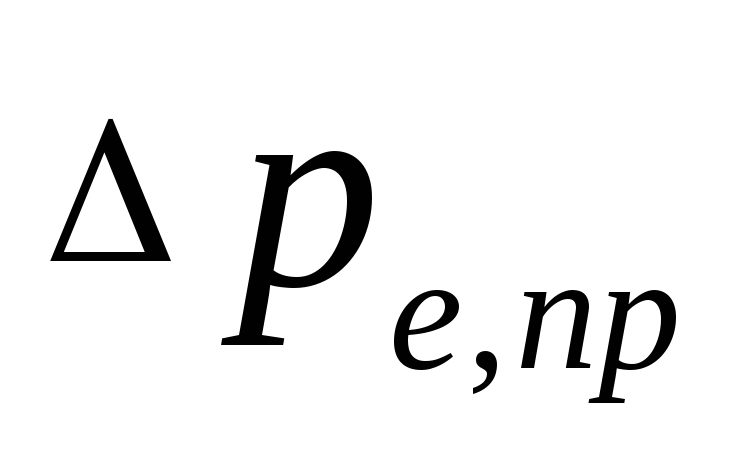
prirodni pritisak koji nastaje kada
vodeno hlađenje u aparatima, Pa, moguće
odrediti kako
 ,
,
(5.3)
gdje
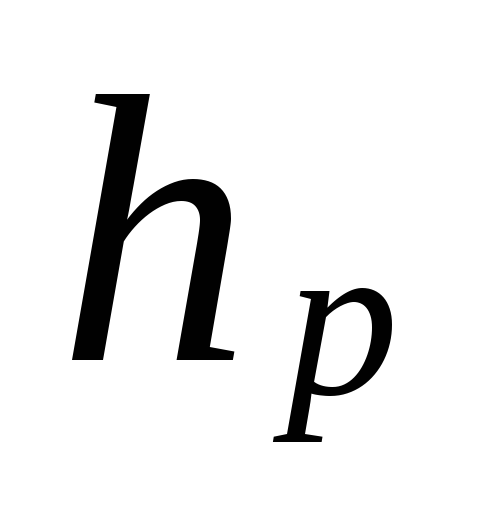
udaljenost od središta pumpe (dizala)
do središta uređaja donjeg kata, m.
Značenje
koeficijent moguće
odrediti iz tablice 5.1.
stol
5.1 - Značenje c
ovisno o projektiranoj temperaturi
vode u sustavu grijanja
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
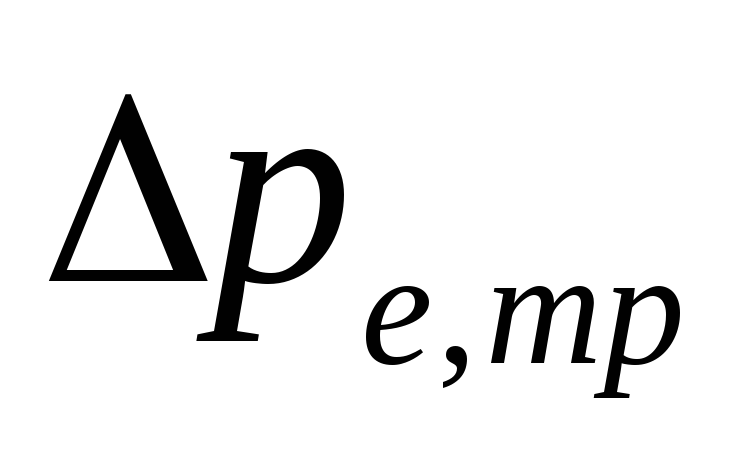
prirodni pritisak u
kao rezultat hlađenja vode u cjevovodima
.
V
crpni sustavi s donjim ožičenjem
veličina
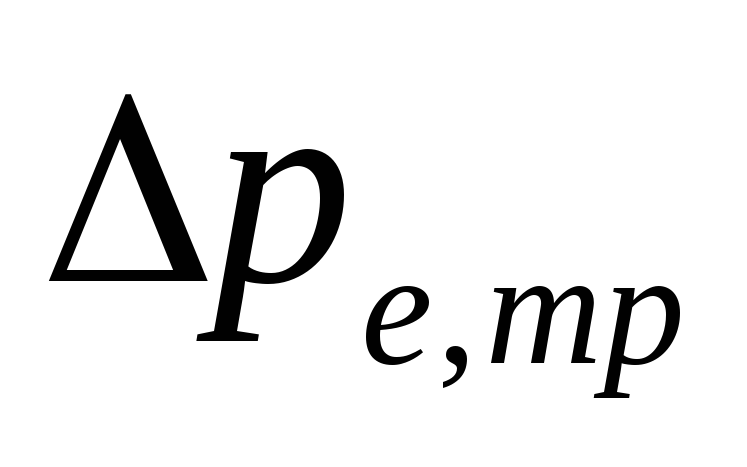
-
Odlučni su
specifični gubitak tlaka trenjem
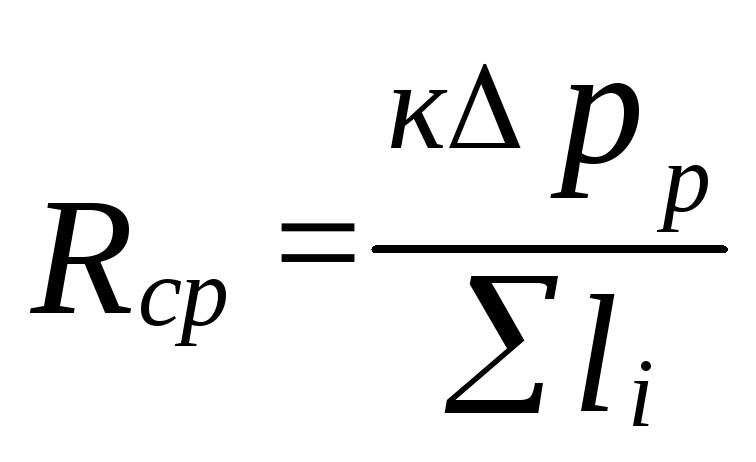
(5.4)
gdje
k=0,65 određuje udio gubitaka tlaka
za trenje.
5.
Protok vode u tom području je određen prema
formula
 (5.5)
(5.5)
gdje
P
- toplinsko opterećenje na gradilištu, W:
(tG
— tO)
- temperaturna razlika rashladne tekućine.
6.
Po veličini
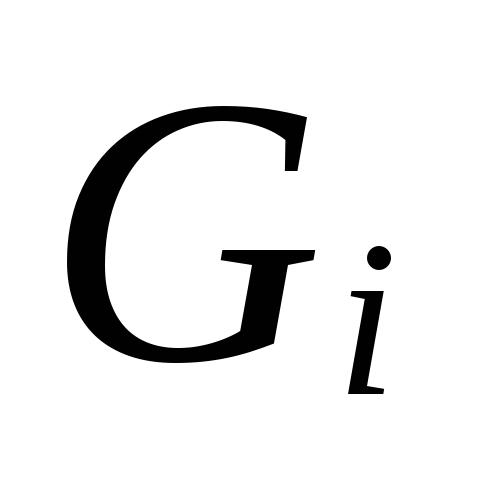
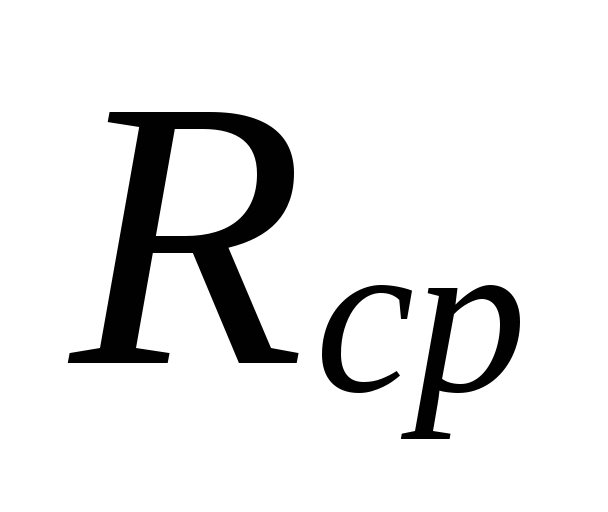
.

6.
Za odabrane promjere cjevovoda
te se utvrđuje procijenjena potrošnja vode
brzina rashladne tekućine v
a stvarna specifična
gubitak tlaka trenjem Rf.
Na
izbor promjera u područjima s malim
brzine protoka rashladne tekućine mogu biti
velika neslaganja između
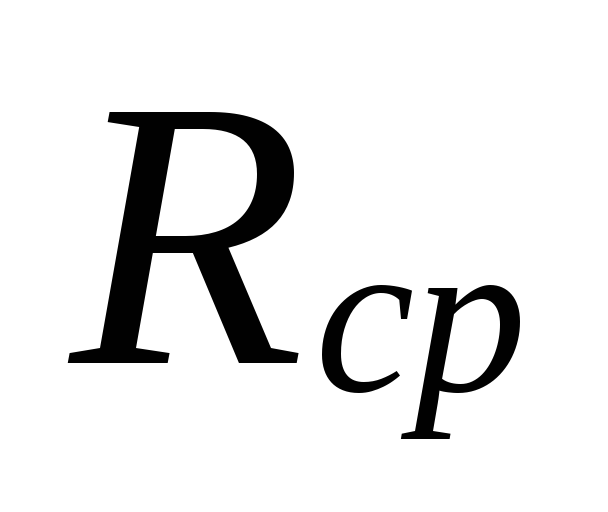
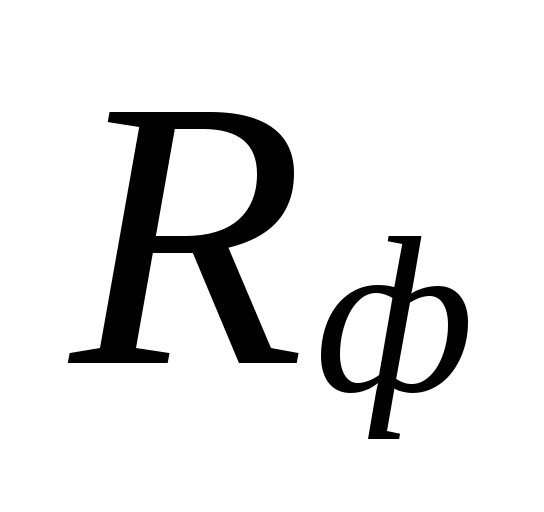
podcijenjeni gubici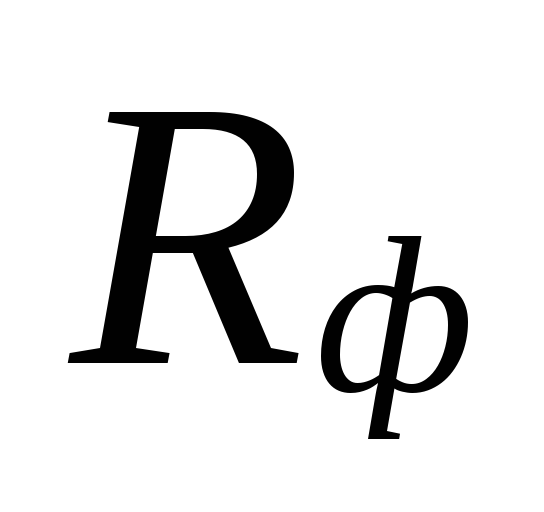
ta su područja nadoknađena precijenjenjem
količine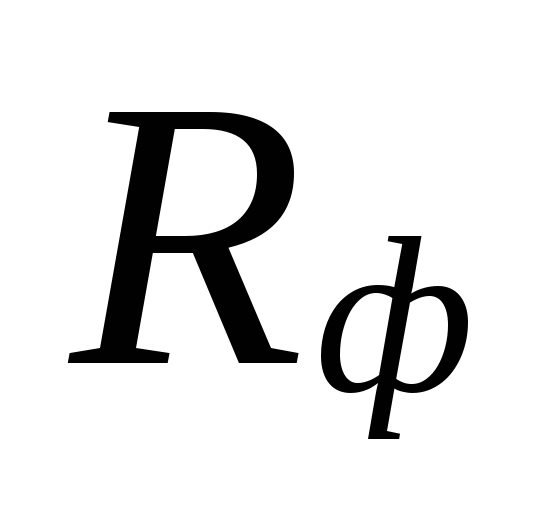
7.
Određuju se gubici tlaka zbog trenja
na izračunatoj površini, Pa:
 .
.
(5.6)
rezultate
proračuni su uneseni u tablicu 5.2.
8.
Gubici tlaka u lokalnoj
otpori pomoću formule:
 ,
,
(5.7)
gdje
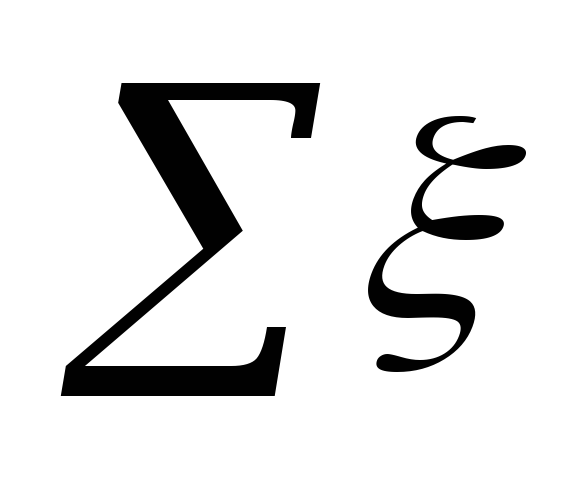
na području naselja.
Značenje ξ
na svakom mjestu sažeti su u tablici. 5.3.
Tablica 5.3 -
Lokalni koeficijenti otpora
|
br. p / str |
Imena |
vrijednosti |
Bilješke |
9.
Odredite ukupni gubitak tlaka
u svakom području
 .
.
(5.8)
10. Odredite
ukupni gubitak tlaka zbog trenja i
u lokalnim otporima u glavnom
cirkulacijski prsten
 .
.
(5.9)
11. Usporedi Δr
S ΔrR.
Ukupni gubitak tlaka u prstenu
mora biti manji od ΔrR
na
 .
.
(5.10)
zaliha jednokratnih
potreban je pritisak na neuračunate in
proračun hidrauličkog otpora.
Ako uvjeti nisu
se izvode, potrebno je na nekima
dijelove prstena za promjenu promjera cijevi.
12. Nakon izračuna
glavni cirkulacijski prsten
spojite preostale prstenove. V
broji se samo svaki novi prsten
dodatna ne-zajednička područja,
spojena paralelno sa sekcijama
glavni prsten.
Neusklađenost gubitka
pritisci na paralelno spojenim
parcele dopuštene do 15% uz slijepu ulicu
kretanje vode i do 5% - s prolaskom.
stol
5.2 - Rezultati hidrauličkog proračuna
za sustav grijanja
|
Na |
Po |
Po |
||||||||||||||
|
Broj |
toplinski |
Potrošnja |
Duljina |
Promjer |
Ubrzati |
Specifično |
Gubici |
Iznos |
Gubici |
d, |
v, |
R, |
Δrtr, |
∑ξ |
Z, |
Rl+Z, |
Lekcija 6
Promjena temperature plina duž duljine plinovoda
U stacionarnom strujanju plina, masa
brzina protoka u plinovodu je
 . (2.41)
. (2.41)
Zapravo, kretanje plina u plinovodu
uvijek nije izotermna. V
Tijekom kompresije plin se zagrijava.
Čak i nakon njegovog hlađenja na COP, temperatura
plin koji ulazi u cjevovod
je oko 2040S,
koja je mnogo viša od temperature
okoliš (T).
U praksi, temperatura plina postaje
blizu temperature okoline
samo za plinovode malog promjera
(Dy0.
Štoviše, treba uzeti u obzir da
plinovodni plin
je pravi plin, koji je svojstven
Joule-Thompsonov efekt, koji uzima u obzir
apsorpcija topline tijekom ekspanzije plina.
Kad se temperatura mijenja po dužini
opisano je kretanje plina u plinovodu
sustav jednadžbi:
specifična energija ,
,
kontinuitet ,
,
Države ,
,
toplinska ravnoteža .
.
Razmotrimo u prvoj aproksimaciji jednadžbu
toplinska ravnoteža bez uzimanja u obzir učinka
Joule Thompson. Integriranje jednadžbe
toplinska ravnoteža
 ,
,
dobivamo
 , (2.42)
, (2.42)
gdje ;
;
KSR- prosjek na stranici pun
koeficijent prijelaza topline od plina do
okoliš;
G je maseni protok plina;
cP–
prosječni izobarični toplinski kapacitet plina.
vrijednosttL se naziva bezdimenzijskim kriterijem
Šuhov
 (2.43)
(2.43)
Dakle, temperatura plina na kraju
plinovod će biti
 . (2.44)
. (2.44)
Na udaljenosti x od početka
utvrđuje se temperatura plina u plinovodu
prema formuli
 . (2.45)
. (2.45)
Promjena temperature duž duljine plinovoda
je eksponencijalna (sl.
2.6).
Smatrati
utjecaj promjene temperature plina na
performanse cjevovoda.
Množenje obje strane specifične jednadžbe
energije na 2 i izražavanje ,
,
dobivamo
 . (2.46)
. (2.46)
Gustoću plina izražavamo na lijevoj strani
izraze (2.46) iz jednadžbe stanja
 ,
,
proizvodwiz jednadžbe kontinuiteta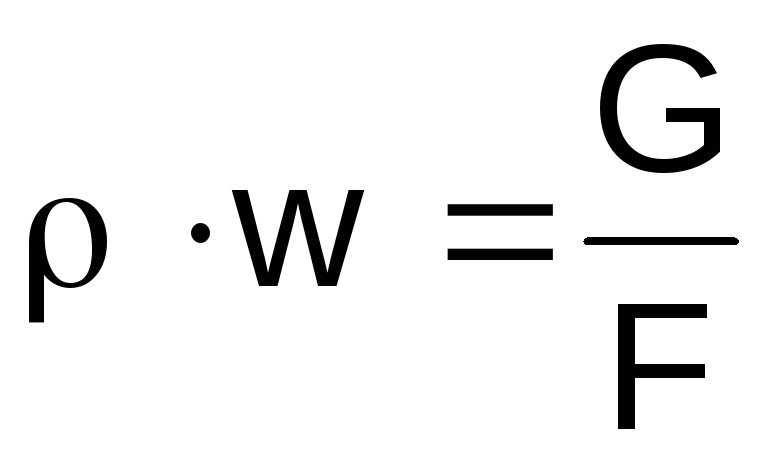
ravnoteža .
.
Imajući to na umu, specifična jednadžba
energija poprima oblik
 (2.47)
(2.47)
ili
 . (2.48)
. (2.48)
Označavajući
 i integriranje lijeve strane jednadžbe
i integriranje lijeve strane jednadžbe
(2,48) iz PHdoPDO, a desno od THtočkaDO, dobivamo
 . (2.49)
. (2.49)
Zamjenom
 , (2.50)
, (2.50)
imamo
 . (2.51)
. (2.51)
Nakon integracije u navedenom
granice, dobivamo

 . (2.52)
. (2.52)
Uzimajući u obzir (2.42)

ili
 , (2.53)
, (2.53)
gdje je korekcijski faktor koji uzima u obzir
je korekcijski faktor koji uzima u obzir
promjena temperature duž duljine plinovoda
(neizotermnost strujanja plina).
Uzimajući u obzir (2.53), ovisnost za određivanje
maseni protok plina će poprimiti oblik
 . (2.54)
. (2.54)
Vrijednost Huvijek veći od jedan, dakle
maseni protok plina pri promjeni
temperatura duž duljine plinovoda
(neizotermni režim strujanja) uvijek
manje nego u izotermnom načinu rada
(T=idem). Proizvod THnaziva se srednjim integralom
temperatura plina u cjevovodu.
S vrijednostima Šuhovljevog broja Shu4
protok plina u cjevovodu
smatrati gotovo izotermnim
na T=idem. Takva temperatura
način rada je moguć pri pumpanju plina sa
niske cijene plinovoda
malog (manje od 500 mm) promjera do značajnog
udaljenosti.
Utjecaj promjene temperature plina
manifestira se za vrijednosti Šuhovljevog broja
Shu
Na
pumpanje plina prisutnost gasa
učinak dovodi do dubljeg
hlađenje plinom nego samo s izmjenom topline
sa zemljom. U ovom slučaju temperatura
plin može čak pasti ispod
temperatura T (sl.
2.7).
Riža. 2.7. Utjecaj Joule-Thompsonovog efekta
o raspodjeli temperature plina preko
duljina cjevovoda
1 - bez uzimanja u obzir Di; 2 - s
uzimajući u obzir Di
Zatim, uzimajući u obzir Joule-Thompsonov koeficijent
zakon promjene temperature po dužini
poprima oblik
 , (2.55)
, (2.55)
5 Hidraulički gubici
Razlika
tlak ulja u dva dijela jednog
i isti cjevovod, pod uvjetom da
prvi se nalazi uzvodno, i
drugi - ispod, određuje se jednadžba
Bernoulli
 ,
,
gdje
h2
– h1
- razlika u visinama težišta
odjeljaka iz proizvoljno odabranog
vodoravna razina;
v1,
v2
– prosječne brzine ulja u dionicama;
g - ubrzanje sile
gravitacija;

hidraulički gubici tijekom kretanja
ulja iz prvog dijela u drugi.
Jednadžba
Bernoulli u punoj upotrebi
za proračun usisnih vodova crpki;
u drugim slučajevima, prvi pojam,
obično se zanemaruje i razmatra:

hidraulički
gubici se obično dijele na lokalne
gubici i gubici od trenja po dužini
cjevovodi (linearni).
1.5.1
lokalni gubici
energije su zbog lokalnih
hidraulički otpor,
uzrokujući izobličenje protoka. Lokalni
otpori su: suženja,
proširenje, zaokruživanje cjevovoda,
filteri, upravljačka oprema i
regulacija i sl. Pri tečenju
tekućine kroz lokalne otpore
brzina mu se mijenja i obično ima
veliki vrtlozi.
Gubici
pritisak lokalnih otpora
određena formulom Weisbach:
 MPa
MPa
(ili
 Godišnje),
Godišnje),
gdje

gubitak,
v
je prosječna brzina strujanja po poprečnom presjeku
u cijevi iza lokalnog otpora, m/s;
,
N/m3;
g=9,81 m/s2.
Svaki
karakteriziran je lokalni otpor
po svojoj vrijednosti koeficijenta

Uz turbulentno strujanje, vrijednosti
otpora i vrlo malo promjena
s promjenom veličine odjeljka, brzine
protok i viskoznost tekućine. Tako
pretpostaviti da ne ovise o broju
Reynolds Re.
vrijednosti

npr. za majice s istim
promjeri kanala uzimaju se jednaki,
ako:
potoci
zbrajati, razilaziti se; teći
pretjecanje;









na
savijanje cijevi

vrijednosti

u hidrauličkim sustavima opreme, preuzeto iz
referentna literatura.
Na
laminarni tok (Re
Gubici
pritisak od lokalnih otpora na
laminarni tok određuju se
formula:
 MPa
MPa
gdje

= a

Količine
gubitak tlaka u standardu
hidraulički uređaji za
nominalni protok obično
navedene u njihovim tehničkim specifikacijama.
1.5.2
Gubitak na
dužinsko trenje
je gubitak energije koji se javlja
u ravnim cijevima konstantnog presjeka,
oni. s ravnomjernim protokom tekućine,
a povećavati proporcionalno duljini
cijevi. Ovi gubici su posljedica internih
trenja u tekućini, pa stoga imaju
stavite u grube i glatke cijevi.
Gubici
tlak trenja cjevovoda
određuje se formulom Darcy:
 MPa
MPa
gdje

l
i d
- duljina i unutarnji promjer cjevovoda,
mm.
Ovaj
formula je primjenjiva i za laminarne,
kao i u turbulentnom strujanju; razlika
sastoji se samo od vrijednosti koeficijenta

Na
laminarni tok (Re
Na
turbulentno strujanje koeficijent trenja
nije samo funkcija Re, nego
također ovisi o hrapavosti unutarnje
površina cijevi. Za hidraulički
glatko, nesmetano cijevi,
oni. s grubošću koja
praktički ne utječe na njegovu otpornost,
koeficijent turbulentnog trenja
način se može odrediti formulom PC.
Konakova:

cijev
smatra se hidraulički glatkim ako
(d/k)>(Re/20),
gdje je k ekvivalentna hrapavost,
mm. Na primjer, za novi bešavni čelik
cijevi k≈0,03
mm, a nakon nekoliko godina rada
k≈0,2
mm, za nove bešavne cijevi od
obojeni metali k≈0,005
mm. Ove cijevi se često koriste u
hidraulički sustavi alatnih strojeva.
Koeficijent
trenje u turbulentnom režimu može biti
odrediti formulom Altshulya,
biti univerzalan (tj. primjenjiv
u svakom slučaju):

2. Karakteristike protoka modula protoka cjevovoda
Prisjetimo se
formula linearnog gubitka - Darcyjeva formula
- Weisbach:
 .
.
Izraziti
u ovoj formuli, brzina V
kroz protok Q
iz omjera
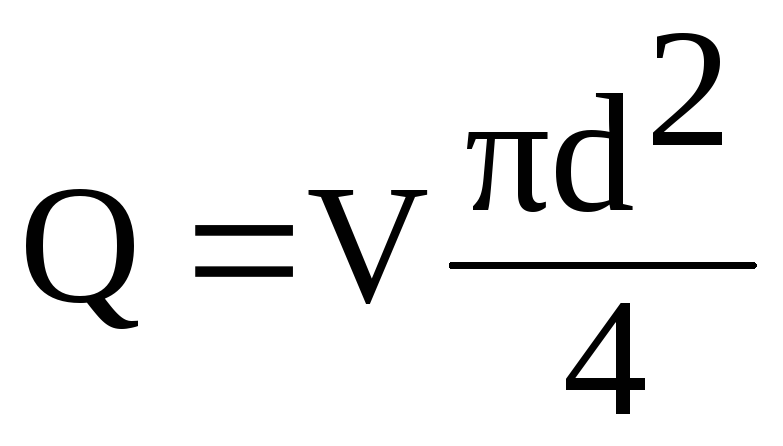
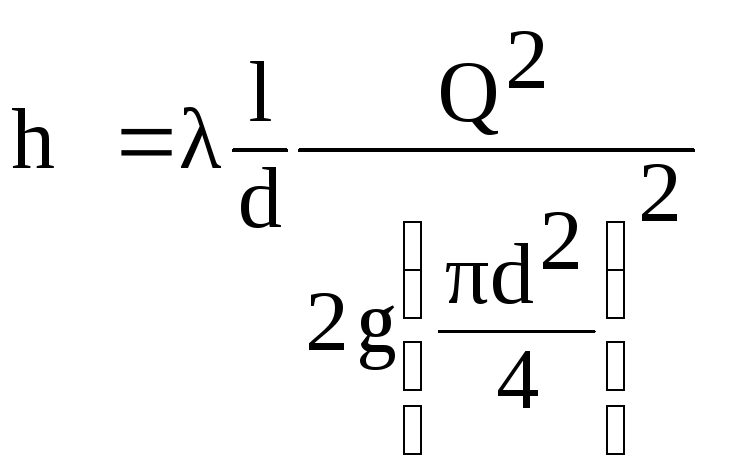
(6.1)
Za
cjevovod određenog promjera
kompleks količina
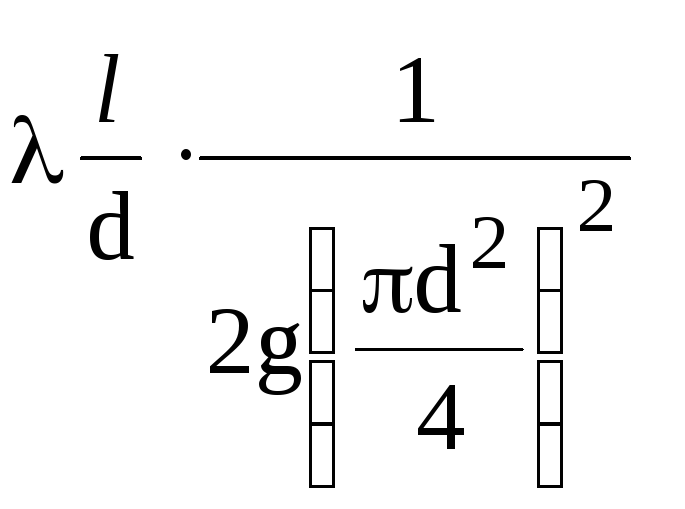
konstanta (1/K2),
osim hidrauličkog koeficijenta
trenje λ. Na temelju koncepta
prosječna ekonomska brzina Vs.e
pokažimo da je naznačeni koeficijent λ
može se pripisati ovom kompleksu, jer v
U ovom slučaju, Reynoldsov broj će biti
imaju specifično značenje:
 ,
,
a na Nikuradzeovom plohu koeficijent λ in
ovaj slučaj će imati specifičnu
značenje.
Opravdati
legitimnost uvođenja pojma
prosječna ekonomska brzina kako slijedi
rasuđivanje.
hidraulički
sustav, kao što je vodovod,
možete preskočiti određeni trošak
izrađene od cijevi različitih promjera. Na
Istovremeno, s povećanjem promjera d,
dakle, smanjenje brzine V
kapitalni izdaci će rasti, i
operativni troškovi će
smanjenje zbog smanjenja hidrauličkog
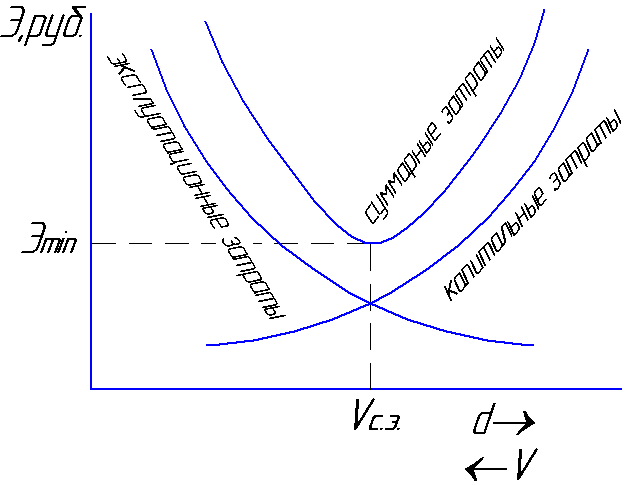
gubici. Brzina kojom se ukupno
troškovi će biti minimalni
nazvat će se prosječnim ekonomskim
brzina Vs.e
= 0,8 ... 1,3 m / s (slika 6.1).
sl.6.1
Zatim
formula linearnog gubitka (6.1) ima oblik
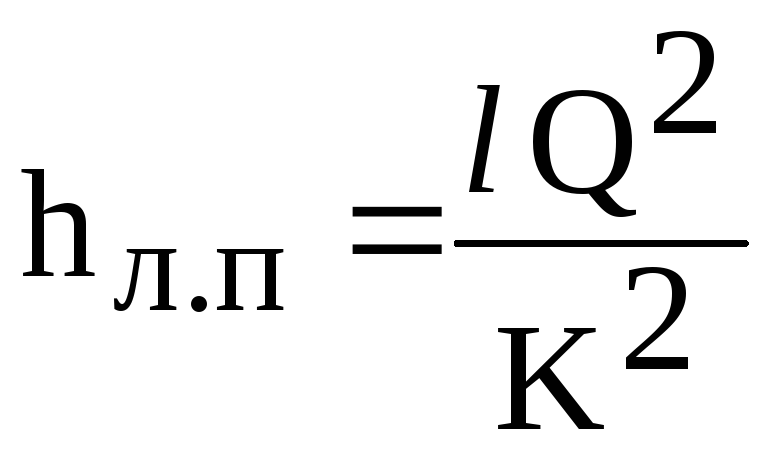
(6.2)
gdje
K - karakteristika protoka cjevovoda
(modul protoka), ovisno o materijalu
cjevovod, promjer i protok. zauzeto je
sa stolova.
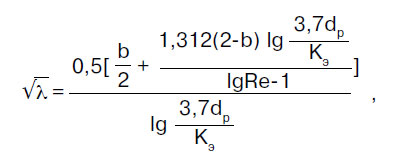
 ), C
), C ,
,