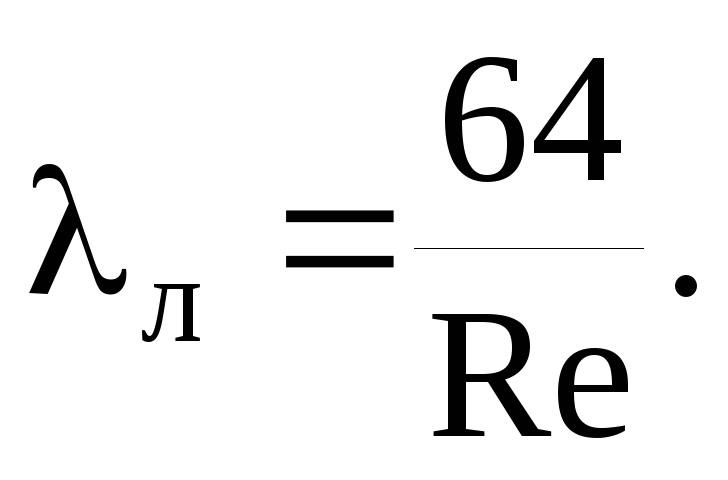1. Ciśnienie hydrostatyczne
Ciśnienie hydrostatyczne wynosi
wewnętrzna siła ściskająca z powodu
przez działanie sił zewnętrznych przyłożonych do
podany punkt w płynie. Taka presja
we wszystkich kierunkach jest taka sama i zależy
na pozycji punktu w płynie w spoczynku.
Wymiar ciśnienia hydrostatycznego
w systemie MKGSS - kg/cm2 lub t/m2,
w układzie SI - N/m2.
Podstawowe wskaźniki jednostkowe
ciśnienie:
|
kg/cm2 |
N/m2 |
|
|
atmosfera techniczna |
1 |
98066,5 |
|
milimetr słupa wody |
0,0001 |
9,80665 |
|
milimetr słupa rtęci |
0,00136 |
133,32 |
W obliczeniach praktycznych 1 techniczny
atmosfera \u003d 1 kg / cm2 \u003d 10 m wody. Sztuka. =
735 mmHg Sztuka. = 98070 N/m2.
Dla nieściśliwego płynu, który jest
w równowadze pod wpływem siły
grawitacja, pełna hydrostatyka
nacisk punktowy:
p=p+

gdzie p jest ciśnieniem na wolnym
powierzchnia cieczy;

wysokość hz powierzchnią
przekrój równy jeden;
h - głębokość zanurzenia
zwrotnica;

Dla niektórych cieczy wartości
ciężar właściwy używany w rozwiązywaniu
zadania podano w załączniku (tab.
P-3).
Wartość nadciśnienia powyżej
atmosferyczne (pa)
zwany manometrycznym, lub
nadciśnienie:

Jeśli nacisk na wolną powierzchnię
równy atmosferycznemu, a następnie nadmiar
ciśnienie pm=

Ciśnienie pod ciśnieniem atmosferycznym
ilość nazywa się próżnią:
rgnojek= pa- R.
Rozwiązanie większości problemów tego
sekcja jest związana z użytkowaniem
podstawowe równanie hydrostatyki

gdzie z jest współrzędną lub
znak punktowy.
1. Ogólne informacje dotyczące obliczeń hydraulicznych rurociągów
Podczas obliczania
rozważane rurociągi
stały, równomierny nacisk
ruch dowolnego płynu
burzliwy reżim, okrągły cylindryczny
Rury. Płyn w rurach ciśnieniowych
jest pod presją i
ich przekroje są całkowicie
wypełniony. Ruch płynu wzdłuż
w wyniku tego powstaje potok
fakt, że ciśnienie na początku jest większe niż
na końcu.
Hydrauliczny
obliczenia dokonywane są w celu określenia
średnica rurociągu D
ze znanym
długość, aby zapewnić pominięcie
określone natężenie przepływu Q
lub ustanowienie
przy danej średnicy i długości wymaganej
ciśnienie i przepływ płynu. Rurociągi
w zależności od długości i wzoru ich
lokalizacje są podzielone na proste
i złożone. Do prostych rurociągów
obejmuje rurociągi, które nie mają
gałęzie na całej długości, ze stałą
ten sam wydatek.
Rurociągi
składają się z rur o tej samej średnicy
na całej długości lub z odcinków rur o różnych
średnice i długości. Ostatni przypadek
odnosi się do połączenia szeregowego.
Proste rurociągi
w zależności od długości z działką lokalną
opory dzielą się na krótkie i
długo. niski
rurociągi
są
rurociągi o dostatecznie krótkiej długości,
w którym lokalny opór
stanowią ponad 10% hydrauliki
utrata długości. Na przykład obejmują:
rury syfonowe, ssące
rury pomp łopatkowych, syfony (ciśnieniowe
rury wodociągowe pod nasypem drogowym),
rurociągi wewnątrz budynków i budowli,
itp.
długo
rurociągi
nazywa
rurociągi są stosunkowo duże
długości, w których utrata głowy na długości
znacznie przewyższa liczbę lokalnych
straty. Straty lokalne to
mniej niż 5
straty na całej długości rurociągu, a co za tym idzie
można je zaniedbywać lub wprowadzać w
obliczenia hydrauliczne zwiększające
współczynnik równy 1,05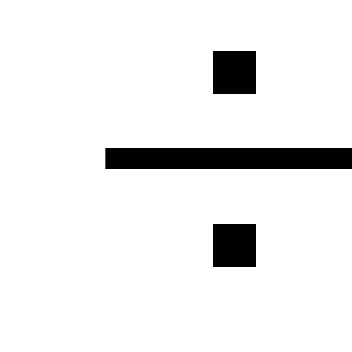
Do systemu wchodzą długie rurociągi
sieci wodociągowe, przewody pompowe
stacje, przewody i rurociągi
przedsiębiorstwa przemysłowe i
cel rolniczy i
itp.
Rurociągi złożone
mają różne gałęzie na całej długości,
tych. rurociąg składa się z sieci rur
określone średnice i długości. Kompleks
rurociągi są podzielone na
równoległy, ślepy zaułek (rozgałęziony),
rurociągi pierścieniowe (zamknięte),
włączone do sieci wodociągowej.
Hydrauliczny
obliczenia rurociągu są redukowane, ponieważ
zwykle do rozwiązania trzech głównych problemów:
-
definicja
przepływ rurociągu Q,
Jeśli jest znany
ciśnienie h,
długość ja
i średnica D
rurociąg,
biorąc pod uwagę dostępność niektórych lokalnych
opory lub w przypadku ich braku; -
definicja
wymagane ciśnienie h,
niezbędne do zabezpieczenia przepustki
znany przepływ Q
rurociągiem
długo ja
i średnica D; -
definicja
średnica rurociągu D
Kiedy
znane wartości głowy h,
koszt Q
i długość ja.
Natężenie przepływu płynu wynosi
gdzie q > obliczeniowy przepływ płynu, m3/s;
- powierzchnia części pod napięciem rury, m2.
Współczynnik oporu tarcia λ określa się zgodnie z przepisami zbioru zasad SP 40-102-2000 „Projektowanie i montaż rurociągów do instalacji wodociągowych i kanalizacyjnych z materiałów polimerowych. Ogólne wymagania":
gdzie b jest pewną liczbą podobieństwa reżimów przepływu płynu; dla b > 2 przyjmuje się b = 2.
gdzie Re jest rzeczywistą liczbą Reynoldsa.
gdzie ν jest współczynnikiem lepkości kinematycznej cieczy, m²/s. Przy obliczaniu rur zimnej wody przyjmuje się, że wynosi 1,31 10-6 m² / s - lepkość wody w temperaturze +10 ° C;
Rekv > - liczba Reynoldsa odpowiadająca początkowi kwadratowego obszaru oporu hydraulicznego.
gdzie Ke jest hydrauliczną chropowatością materiału rury, m. Dla rur wykonanych z materiałów polimerowych przyjmuje się Ke = 0,00002 m, jeśli producent rury nie podaje innych wartości chropowatości.
W tych przypadkach przepływu, gdy Re ≥ Rekv, obliczona wartość parametru b staje się równa 2, a wzór (4) ulega znacznemu uproszczeniu, zamieniając się w dobrze znaną formułę Prandtla:
Przy Ke = 0,00002 m kwadratowy obszar oporu występuje przy natężeniu przepływu wody (ν = 1,31 10-6 m²/s) równym 32,75 m/s, co jest praktycznie nieosiągalne w publicznych sieciach wodociągowych.
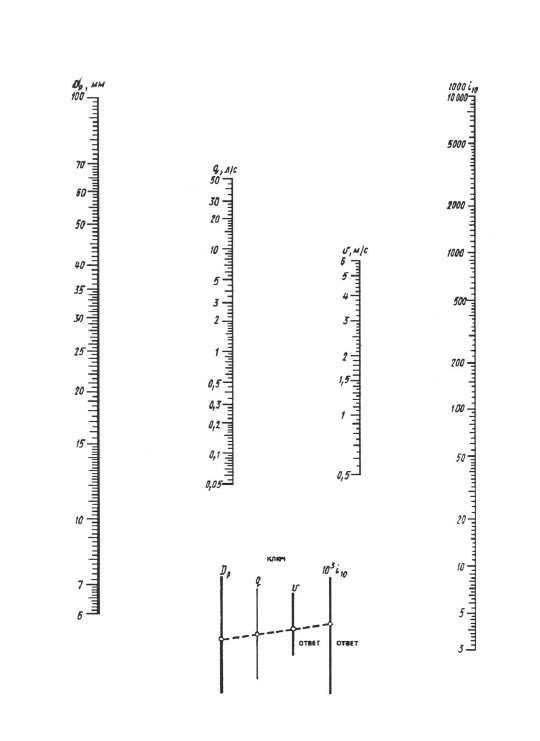
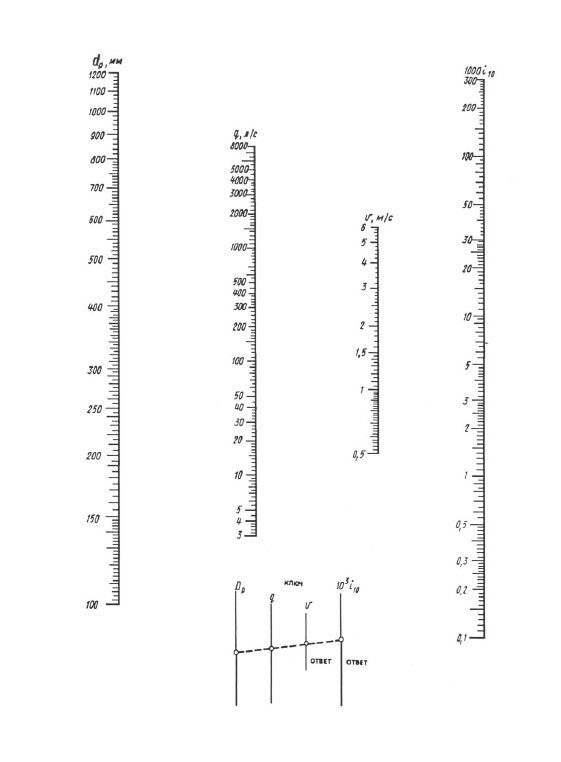
Do codziennych obliczeń zalecane są nomogramy, a do dokładniejszych obliczeń - „Tabele do obliczeń hydraulicznych rurociągów wykonanych z materiałów polimerowych”, tom 1 „Rurociągi ciśnieniowe” (A.Ya. Dobromyslov, M., VNIIMP, 2004).
Przy obliczaniu według nomogramów wynik uzyskuje się za pomocą jednej nakładki linijki - należy połączyć punkt z wartością obliczonej średnicy na skali dp z punktem z wartością obliczonego natężenia przepływu na q (l / s) skalować linią prostą, kontynuować tę linię aż do przecięcia się z podziałkami prędkości V i głowicy strat jednostkowych 1000 i (mm/m). Punkty przecięcia prostej z tymi podziałkami dają wartości V oraz 1000 i.
Jak wiadomo, koszt energii elektrycznej do pompowania cieczy jest wprost proporcjonalny do wartości H (ceteris paribus). Podstawiając wyrażenie ( 3 ) do wzoru ( 2 ), łatwo zauważyć, że wartość i (iw konsekwencji H) jest odwrotnie proporcjonalna do obliczonej średnicy dp do piątego stopnia.
Powyżej pokazano, że wartość dp zależy od grubości ścianki rury e: im cieńsza ścianka, tym większe dp i odpowiednio mniejsza strata ciśnienia na skutek tarcia i koszt energii elektrycznej.
Jeśli wartość MRS rury zmieni się z jakiegokolwiek powodu, należy ponownie obliczyć jej średnicę i grubość ścianki (SDR).
Należy pamiętać, że w wielu przypadkach zastosowanie rur z MRS 10 zamiast rur z MRS 8, zwłaszcza rur z MRS 6,3, umożliwia zmniejszenie średnicy rurociągu o jeden rozmiar. Dlatego w naszych czasach stosowanie polietylenu PE 80 (MRS 8) i PE 100 (MRS 10) zamiast polietylenu PE 63 (MRS 6.3) do produkcji rur pozwala nie tylko zmniejszyć grubość ścianki rur, ich wagę i zużycie materiałów, ale także w celu zmniejszenia kosztów energii do pompowania cieczy (ceteris paribus).
W ostatnich latach (po 2013 roku) rury wykonane z polietylenu PE80 zostały prawie całkowicie zastąpione z produkcji rurami wykonanymi z polietylenu gatunku PE100. Tłumaczy się to tym, że surowce, z których wykonane są rury, sprowadzane są z zagranicy pod marką PE100.A także dlatego, że gatunek polietylenu 100 ma więcej właściwości wytrzymałościowych, dzięki czemu produkowane są rury o takich samych właściwościach jak rury wykonane z PE80, ale o cieńszej ściance, zwiększając w ten sposób przepustowość rurociągów polietylenowych.
Nomogram do określania strat ciśnienia w rurach o średnicach 6,100 mm.
Nomogram do określania strat ciśnienia w rurach o średnicach 100, 1200 mm.
Kryterium Reynoldsa
Zależność tę wydobył angielski fizyk i inżynier Osborne Reynolds (1842-1912).
Kryterium pomagającym odpowiedzieć na pytanie, czy należy brać pod uwagę lepkość, jest liczba Reynoldsa Re. Jest on równy stosunkowi energii ruchu elementu przepływającego płynu do pracy sił tarcia wewnętrznego.
Rozważmy płynny element sześcienny o długości krawędzi n. Energia kinetyczna elementu to:
Zgodnie z prawem Newtona siła tarcia działająca na element płynny jest zdefiniowana w następujący sposób:
Praca tej siły podczas przemieszczania elementu płynu na odległość n wynosi
a stosunek energii kinetycznej elementu płynu do pracy siły tarcia wynosi
Redukujemy i otrzymujemy:
Re nazywa się liczbą Reynoldsa.
Tak więc Re jest wielkością bezwymiarową, która charakteryzuje względną rolę sił lepkości.
Na przykład, jeśli wymiary ciała, z którym styka się ciecz lub gaz, są bardzo małe, to nawet przy niskiej lepkości Re będzie nieznaczne, a siły tarcia będą odgrywać dominującą rolę. Wręcz przeciwnie, jeśli wymiary ciała i prędkość są duże, to Re >> 1, a nawet duża lepkość nie będą miały prawie żadnego wpływu na charakter ruchu.
Jednak nie zawsze duże liczby Reynoldsa oznaczają, że lepkość nie odgrywa żadnej roli. Tak więc, gdy zostanie osiągnięta bardzo duża (kilkadziesiąt lub setki tysięcy) wartość liczby Re, płynny przepływ laminarny (z łacińskiej blaszki - „płyta”) zamienia się w turbulentny (z łacińskiego turbulentus - „burzowy” , „chaotyczny”), któremu towarzyszą chaotyczne, niestabilne ruchy płynów. Efekt ten można zaobserwować, stopniowo otwierając kran: cienki strumień zwykle płynie płynnie, ale wraz ze wzrostem prędkości wody zaburza się płynność przepływu. W strumieniu wypływającym pod wysokim ciśnieniem cząsteczki cieczy poruszają się losowo, oscylując, każdemu ruchowi towarzyszy silne mieszanie.
Pojawienie się turbulencji znacznie zwiększa opór. W rurociągu prędkość przepływu turbulentnego jest mniejsza niż prędkość przepływu laminarnego przy tych samych spadkach ciśnienia. Ale turbulencje nie zawsze są złe. Ze względu na to, że mieszanie podczas turbulencji jest bardzo duże, wymiana ciepła – chłodzenie lub nagrzewanie kruszyw – zachodzi znacznie intensywniej; reakcje chemiczne rozprzestrzeniają się szybciej.
Równanie ruchu stacjonarnego Bernoulliego
Jedno z najważniejszych równań hydromechaniki uzyskał w 1738 roku szwajcarski naukowiec Daniel Bernoulli (1700-1782). Najpierw udało mu się opisać ruch płynu idealnego, wyrażony wzorem Bernoulliego.
Płyn idealny to płyn, w którym nie występują siły tarcia pomiędzy elementami płynu idealnego, a także pomiędzy płynem idealnym a ściankami naczynia.
Równanie ruchu stacjonarnego, które nosi jego imię, to:
gdzie P to ciśnienie cieczy, ρ to jej gęstość, v to prędkość ruchu, g to przyspieszenie swobodnego spadania, h to wysokość, na której znajduje się element cieczy.
Znaczenie równania Bernoulliego jest takie, że w układzie wypełnionym cieczą (odcinek rurociągu) całkowita energia każdego punktu jest zawsze niezmieniona.
Równanie Bernoulliego ma trzy wyrazy:
- ρ⋅v2/2 - ciśnienie dynamiczne - energia kinetyczna na jednostkę objętości płynu napędowego;
- ρ⋅g⋅h - ciężar ciśnienie - energia potencjalna jednostki objętości cieczy;
- P - ciśnienie statyczne, w swoim pochodzeniu jest pracą sił nacisku i nie stanowi rezerwy żadnego specjalnego rodzaju energii („energia ciśnienia”).
Równanie to wyjaśnia, dlaczego w wąskich odcinkach rury prędkość przepływu wzrasta, a ciśnienie na ściankach rury maleje. Maksymalne ciśnienie w rurach jest ustawione dokładnie w miejscu, w którym rura ma największy przekrój. Wąskie części rury są pod tym względem bezpieczne, ale ciśnienie w nich może spaść tak bardzo, że ciecz zagotuje się, co może prowadzić do kawitacji i zniszczenia materiału rury.
Równanie Naviera-Stokesa dla lepkich cieczy
W bardziej rygorystycznym sformułowaniu liniowa zależność tarcia lepkiego od zmiany prędkości płynu nazywana jest równaniem Naviera-Stokesa. Uwzględnia ściśliwość cieczy i gazów i w przeciwieństwie do prawa Newtona obowiązuje nie tylko w pobliżu powierzchni ciała stałego, ale także w każdym punkcie cieczy (w pobliżu powierzchni ciała stałego w przypadku nieściśliwego ciała stałego). ciecz, równanie Naviera-Stokesa i prawo Newtona pokrywają się).
Wszelkie gazy, dla których spełniony jest warunek ośrodka ciągłego, są również zgodne z równaniem Naviera-Stokesa, tj. są płynami newtonowskimi.
Lepkość cieczy i gazów jest zwykle znacząca przy stosunkowo niskich prędkościach, dlatego czasami mówi się, że hydrodynamika Eulera jest szczególnym (ograniczającym) przypadkiem wysokich prędkości hydrodynamiki Naviera-Stokesa.
Przy niskich prędkościach, zgodnie z prawem tarcia lepkościowego Newtona, siła oporu ciała jest proporcjonalna do prędkości. Przy dużych prędkościach, gdy lepkość przestaje odgrywać znaczącą rolę, opór ciała jest proporcjonalny do kwadratu prędkości (którą po raz pierwszy odkrył i udowodnił Newton).
Sekwencja obliczeń hydraulicznych
1.
Wybrano główny obieg
system ogrzewania pierścieniowego (większość
niekorzystnie położony w układzie hydraulicznym
relacja). W ślepym zaułku dwururowym
systemy to przechodzący pierścień
dolny instrument najbardziej odległego i
obciążony pion, w pojedynczej rurze -
przez najbardziej odległe i załadowane
pion.
Na przykład,
w dwururowym systemie grzewczym z
górne okablowanie główny obieg
pierścień przejdzie z punktu ciepła
przez główny pion, przewód zasilający,
przez najbardziej oddalony pion, ogrzewanie
urządzenie na dole, linia powrotna
do punktu grzewczego.
V
systemy z towarzyszącym ruchem wody w
pierścień jest traktowany jako główny,
przechodząc przez środek najbardziej
załadowany stojak.
2.
Główny pierścień cyrkulacyjny pęka
na działki (działka jest scharakteryzowana)
stały przepływ wody i to samo
średnica). Schemat pokazuje
numery przekrojów, ich długości i termiczne
masa. Obciążenie cieplne głównego
działki określa się sumując
obsługiwane przez nie obciążenia termiczne
działki. Aby wybrać średnicę rury
stosuje się dwie ilości:
a)
dany przepływ wody;
b)
przybliżone jednostkowe straty ciśnienia
do tarcia w obiegu projektowym
pierścień rPoślubić.
Do
obliczenie rcp
musisz znać długość głównej
pierścień cyrkulacyjny i obliczony
ciśnienie cyrkulacji.
3.
Obliczony obieg
ciśnienie formuły
 ,
,
(5.1)
gdzie
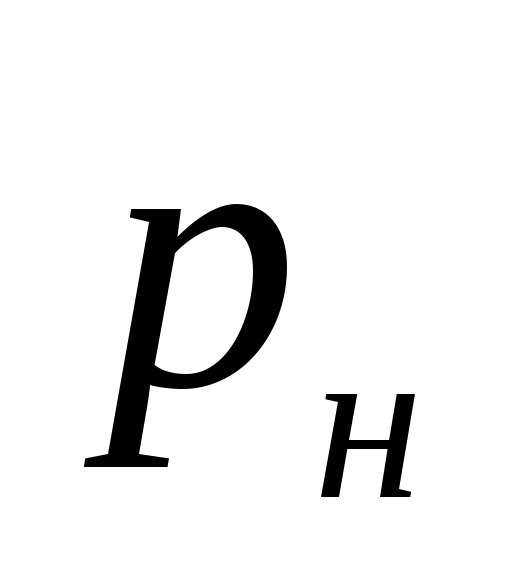
ciśnienie wytwarzane przez pompę, Pa.
Praktyka projektowania systemów
ogrzewanie pokazało, że najbardziej
wskazane jest zmierzenie ciśnienia pompy,
równy
 ,
,
(5.2)
gdzie
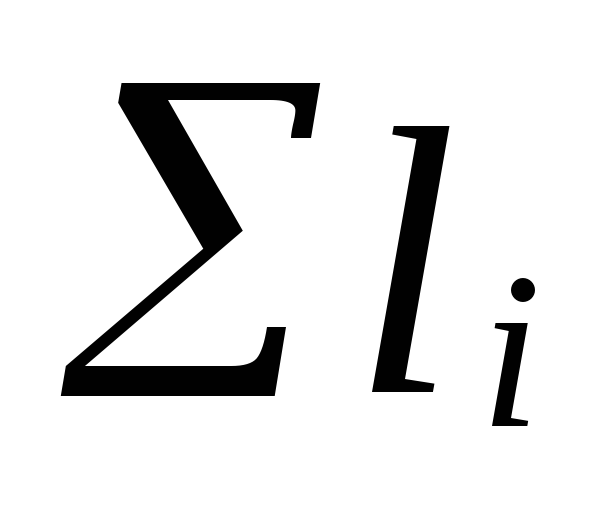
suma długości odcinków głównego obiegu
pierścienie;
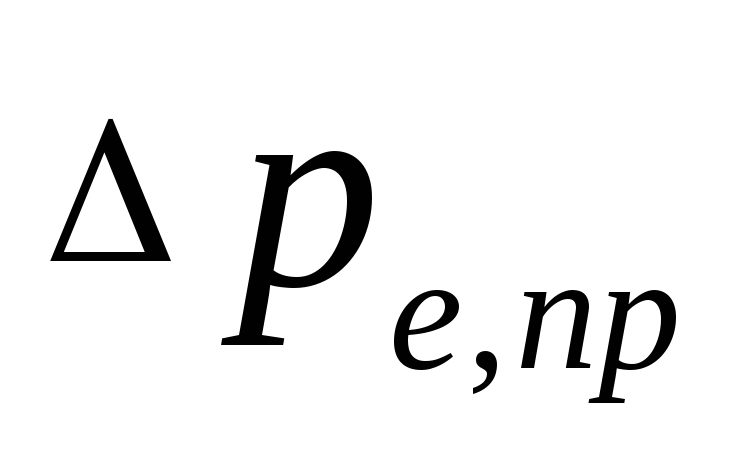
naturalne ciśnienie, które występuje, gdy
chłodzenie wodne w urządzeniach, Pa, możliwe
określić jak
 ,
,
(5.3)
gdzie
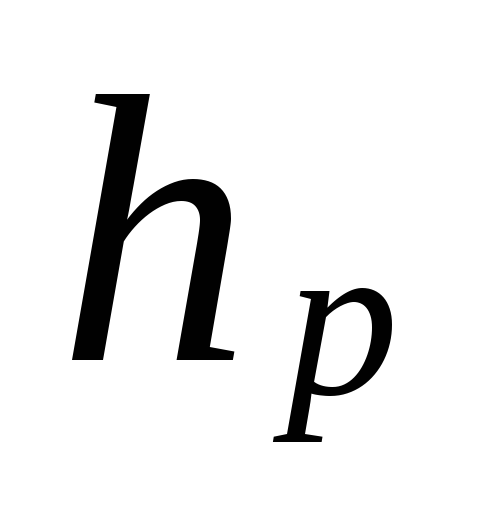
odległość od środka pompy (windy)
do środka urządzenia na dolnym piętrze, m.
Oznaczający
współczynnik możliwe
określić z tabeli 5.1.
Tabela
5.1 - Znaczenie c
w zależności od temperatury projektowej
woda w systemie grzewczym
|
( |
|
|
85-65 |
0,6 |
|
95-70 |
0,64 |
|
105-70 |
0,66 |
|
115-70 |
0,68 |
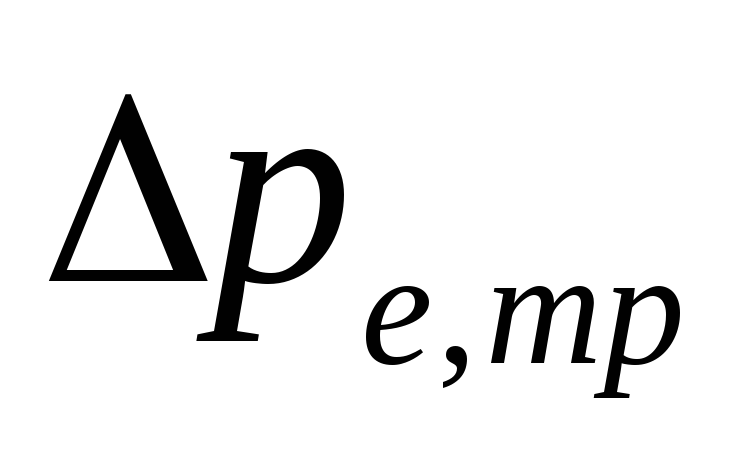
naturalne ciśnienie w
w wyniku chłodzenia wodą w rurociągach
.
V
systemy pompowe z dolnym okablowaniem
ogrom
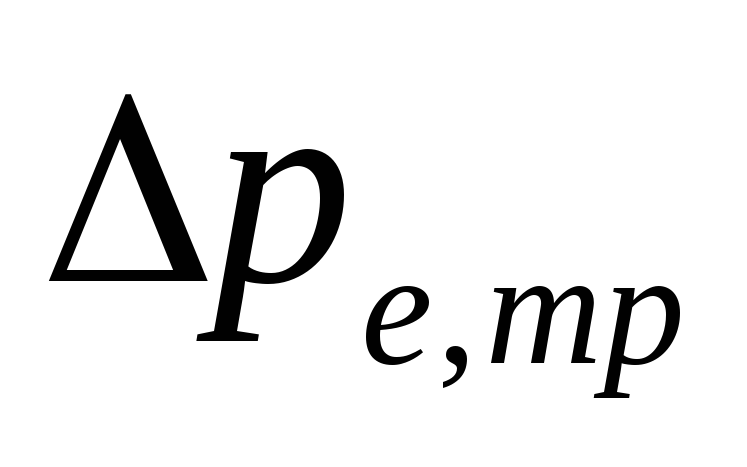
-
Są zdeterminowani
specyficzna strata ciśnienia tarcia
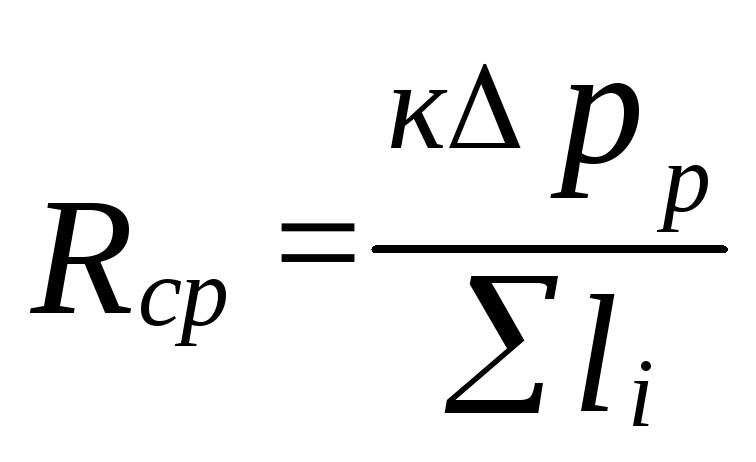
(5.4)
gdzie
k=0,65 określa udział strat ciśnienia
na tarcie.
5.
Przepływ wody w okolicy jest determinowany przez
formuła
 (5.5)
(5.5)
gdzie
Q
- obciążenie cieplne obiektu, W:
(Tg
- TO)
- różnica temperatur chłodziwa.
6.
Według wielkości
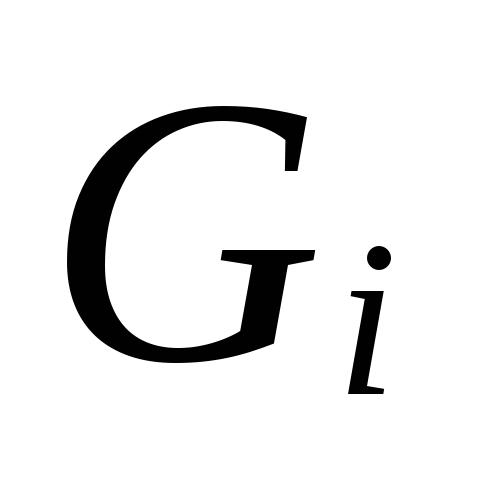
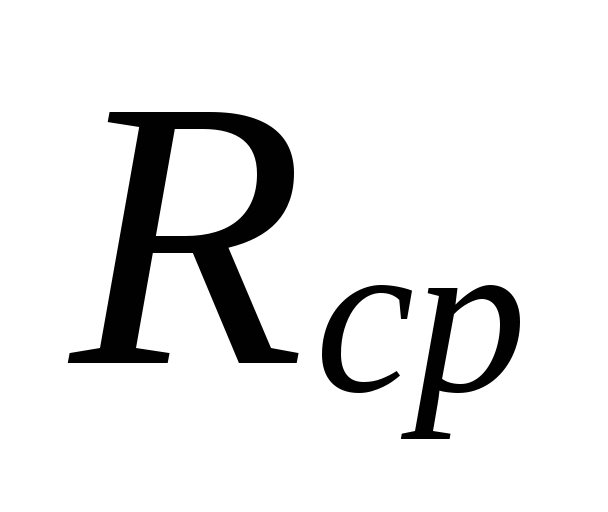
.

6.
Dla wybranych średnic rurociągów
i określa się szacunkowe zużycie wody
prędkość chłodziwa v
a rzeczywista specyfika
utrata ciśnienia tarcia rF.
Na
dobór średnic w obszarach o małych
szybkości przepływu chłodziwa mogą być
duże rozbieżności między
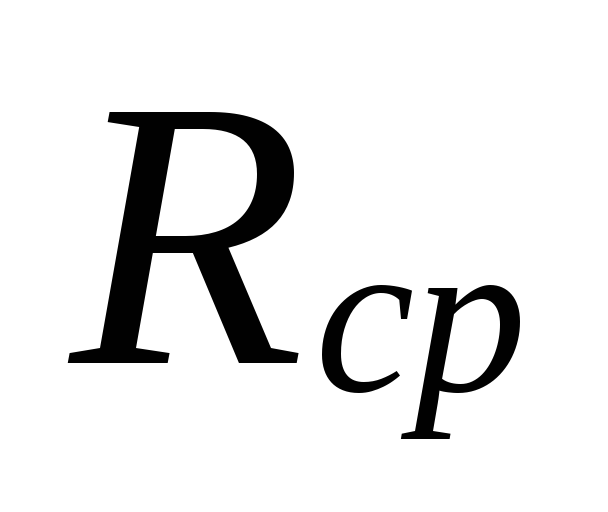
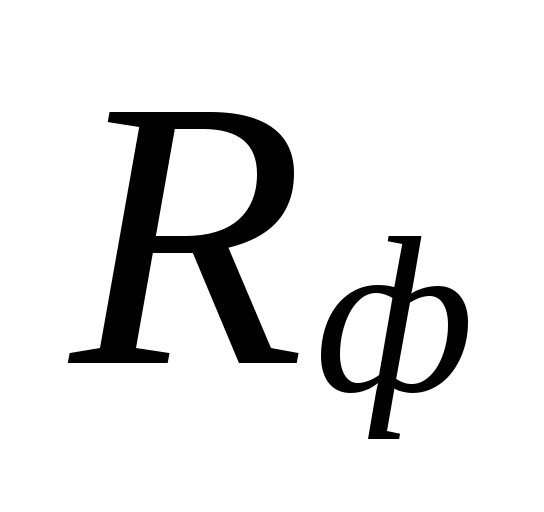
niedoszacowane straty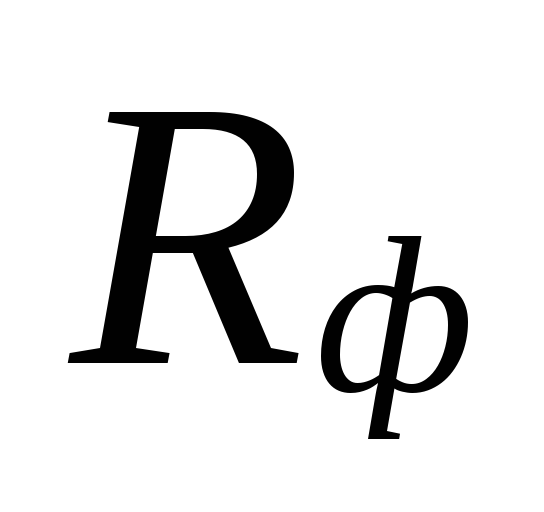
obszary te są kompensowane przeszacowaniem
wielkie ilości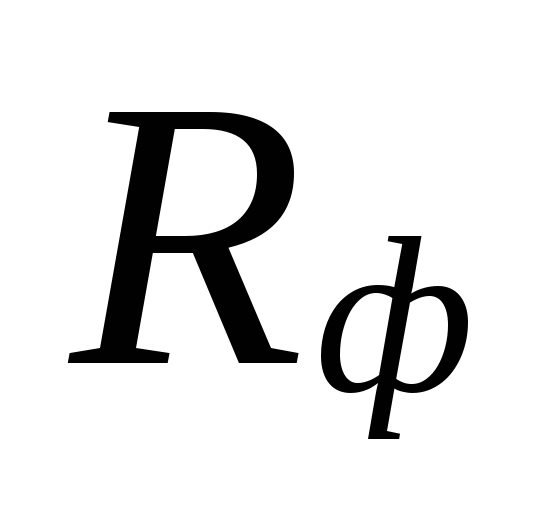
7.
Określane są straty ciśnienia tarcia
na obliczonej powierzchni, Pa:
 .
.
(5.6)
wyniki
obliczenia podano w tabeli 5.2.
8.
Straty ciśnienia w lokalnych
opory za pomocą wzoru:
 ,
,
(5.7)
gdzie
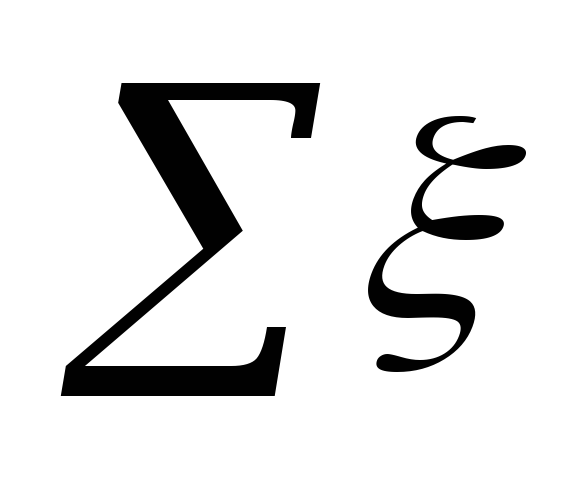
na terenie osady.
Oznaczający ξ.
w każdym miejscu są podsumowane w tabeli. 5.3.
Tabela 5.3 -
Lokalne współczynniki oporu
|
Nr p / p |
Nazwy |
Wartości |
Uwagi |
9.
Określ całkowitą stratę ciśnienia
w każdym obszarze
 .
.
(5.8)
10. Określ
całkowity spadek ciśnienia spowodowany tarciem i
w lokalnych oporach w głównych
pierścień cyrkulacyjny
 .
.
(5.9)
11. Porównaj p
Z pr.
Całkowita strata ciśnienia na pierścieniu
musi być mniejsza niż pr
na
 .
.
(5.10)
zapas jednorazowych
ciśnienie jest potrzebne na niewyjaśnione in
obliczanie oporu hydraulicznego.
Jeśli warunki nie są
są wykonywane, na niektórych jest to konieczne
sekcje pierścienia do zmiany średnic rur.
12. Po obliczeniach
główny pierścień cyrkulacyjny
wykonaj połączenie pozostałych pierścieni. V
liczy się tylko każdy nowy dzwonek
dodatkowe powierzchnie wspólne,
połączone równolegle z sekcjami
pierścień główny.
Rozbieżność strat
ciśnienia na połączeniu równoległym
działki dozwolone do 15% ze ślepym zaułkiem
ruch wody i do 5% - z przechodzeniem.
Tabela
5.2 - Wyniki obliczeń hydraulicznych
do systemu grzewczego
|
Na |
Za pomocą |
Za pomocą |
||||||||||||||
|
Numer |
termiczny |
Konsumpcja |
Długość |
Średnica |
Prędkość |
Konkretny |
Straty |
Suma |
Straty |
D, |
v, |
r, |
ptr, |
∑ξ. |
Z, |
Rl+Z, |
Lekcja 6
Zmiana temperatury gazu na długości gazociągu
W stacjonarnym przepływie gazu masa
natężenie przepływu w gazociągu wynosi
 . (2.41)
. (2.41)
W rzeczywistości ruch gazu w gazociągu
jest zawsze nieizotermiczna. V
Podczas sprężania gaz nagrzewa się.
Nawet po schłodzeniu w COP temperatura
gaz wchodzący do rurociągu
wynosi około 2040С,
co jest znacznie wyższe niż temperatura
środowisko (T).
W praktyce temperatura gazu staje się
zbliżona do temperatury otoczenia
tylko dla gazociągów o małej średnicy
(Dy0.
Ponadto należy wziąć pod uwagę, że
gaz z rurociągów
jest prawdziwym gazem, który jest nieodłączny
efekt Joule'a-Thompsona, który uwzględnia
absorpcja ciepła podczas rozprężania gazu.
Gdy temperatura zmienia się na całej długości
opisano ruch gazu w gazociągu
układ równań:
specyficzna energia ,
,
ciągłość ,
,
stany ,
,
bilans cieplny .
.
Rozważ w pierwszym przybliżeniu równanie
bilans cieplny bez uwzględnienia efektu
Joule'a Thompsona. Całkowanie równania
bilans cieplny
 ,
,
dostajemy
 , (2.42)
, (2.42)
gdzie ;
;
KSR- średnia na stronie pełna
współczynnik przenikania ciepła z gazu do
środowisko;
G to masowe natężenie przepływu gazu;
CP–
średnia izobaryczna pojemność cieplna gazu.
wartośćTL nazywamy kryterium bezwymiarowym
Szuchow
 (2.43)
(2.43)
Czyli temperatura gazu na końcu
gazociąg będzie
 . (2.44)
. (2.44)
W odległości x od początku
określana jest temperatura gazu w gazociągu
według wzoru
 . (2.45)
. (2.45)
Zmiana temperatury na całej długości gazociągu
jest wykładnicza (ryc.
2.6).
Rozważać
wpływ zmiany temperatury gazu na
wydajność rurociągu.
Mnożenie obu stron określonego równania
energia na 2 i wyrażanie ,
,
dostajemy
 . (2.46)
. (2.46)
Wyrażamy gęstość gazu po lewej stronie
wyrażenia (2.46) z równania stanu
 ,
,
iloczyn (z równania ciągłości)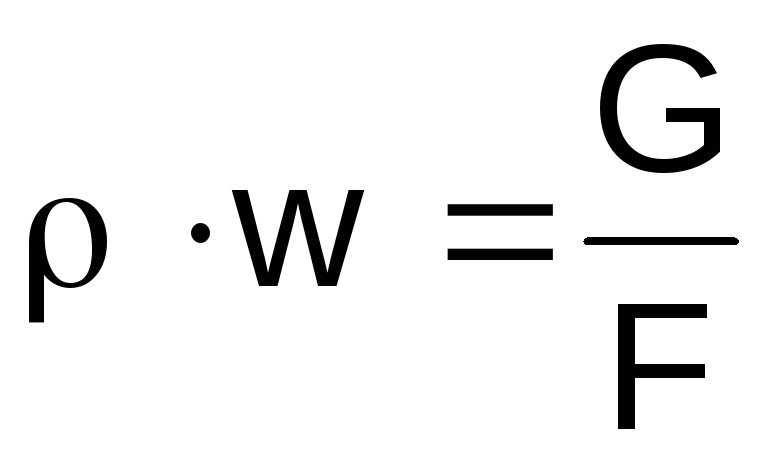
balansować .
.
Mając to na uwadze, szczegółowe równanie
energia przybiera formę
 (2.47)
(2.47)
lub
 . (2.48)
. (2.48)
Oznaczanie
 i całkowanie lewej strony równania
i całkowanie lewej strony równania
(2.48) z PhDOPDOi na prawo od ThkropkaDO, dostajemy
 . (2.49)
. (2.49)
Zastępując
 , (2.50)
, (2.50)
mamy
 . (2.51)
. (2.51)
Po zintegrowaniu w określonym
limity, otrzymujemy

 . (2.52)
. (2.52)
Biorąc pod uwagę (2.42)

lub
 , (2.53)
, (2.53)
gdzie jest współczynnikiem korygującym, który uwzględnia
jest współczynnikiem korygującym, który uwzględnia
zmiana temperatury na długości gazociągu
(nieizotermalność przepływu gazu).
Biorąc pod uwagę (2.53) zależność wyznaczania
masowe natężenie przepływu gazu przyjmie postać
 . (2.54)
. (2.54)
Wartość hzawsze większe niż jeden, więc
masowe natężenie przepływu gazu podczas wymiany
temperatura na całej długości gazociągu
(przepływ nieizotermiczny) zawsze
mniej niż w trybie izotermicznym
(T=idem). Produkt Thnazywana jest całką średnią
temperatura gazu w rurociągu.
Z wartościami liczby Shukhov Shu4
przepływ gazu w rurociągu
uważaj za prawie izotermiczne
w T=idem. Taka temperatura
tryb jest możliwy podczas pompowania gazu z
niskie koszty gazociągów
mała (mniej niż 500 mm) średnica do znacznej
dystans.
Wpływ zmiany temperatury gazu
przejawia się dla wartości liczby Szuchowa
Szu
Na
pompowanie gazu obecność przepustnicy
efekt prowadzi do głębszego
chłodzenie gazowe niż tylko z wymianą ciepła
z glebą. W tym przypadku temperatura
gaz może nawet spaść poniżej
temperatura T (rys.
2.7).
Ryż. 2.7. Wpływ efektu Joule'a-Thompsona
na rozkładzie temperatury gazu powyżej
długość rurociągu
1 - bez uwzględnienia Di; 2 - z
biorąc pod uwagę Di
Następnie, biorąc pod uwagę współczynnik Joule'a-Thompsona
prawo zmian temperatury na długości
przybiera formę
 , (2.55)
, (2.55)
5 Straty hydrauliczne
Różnica
ciśnienie oleju w dwóch sekcjach jednej
i tym samym rurociągiem, pod warunkiem, że
pierwszy znajduje się w górę rzeki, a
drugi - poniżej, jest określony równanie
Bernoulli
 ,
,
gdzie
h2
- h1
- różnica wysokości środków ciężkości
sekcje z dowolnie wybranego
pozioma;
v1,
v2
– średnie prędkości oleju na odcinkach;
g - siła przyspieszenia
powaga;

straty hydrauliczne podczas ruchu
oleje z pierwszej sekcji do drugiej.
Równanie
Bernoulli w pełni wykorzystany
do obliczania linii ssących pomp;
w pozostałych przypadkach pierwszy termin,
zwykle zaniedbywane i brane pod uwagę:

hydrauliczny
straty są zwykle dzielone na lokalne
straty i straty tarcia na długości
rurociągi (liniowe).
1.5.1
lokalne straty
energie wynikają z lokalnych
opór hydrauliczny,
powodując zakłócenia przepływu. Lokalny
opory to: zwężenia,
rozszerzanie, zaokrąglanie rurociągów,
filtry, urządzenia sterujące i
regulacja itp. Podczas przepływu
płyny przez lokalne opory
jego prędkość się zmienia i zwykle są
duże wiry.
Straty
presja lokalnych oporów
określony przez formułę Weisbach:
 MPa
MPa
(lub
 Rocznie),
Rocznie),
gdzie

strata,
v
to średnia prędkość przepływu w przekroju
w rurze za lokalnym oporem, m/s;
,
N/m3;
g=9,81 m/s2.
Każdy
scharakteryzowano lokalny opór
przez jego wartość współczynnika

Przy przepływie turbulentnym wartości
opór i niewiele się zmienia
ze zmianą wielkości przekroju, prędkości
przepływ płynu i lepkość. Więc
załóżmy, że nie zależą od liczby
Reynolds Re.
Wartości

na przykład dla trójników z tym samym
średnice kanałów są traktowane jako równe,
Jeśli:
strumienie
sumować, rozchodzić się; pływ
przechodzący;









w
zgięcie rury

Wartości

w układach hydraulicznych urządzeń, pobrane z
literatura referencyjna.
Na
przepływ laminarny (Re
Straty
ciśnienie od lokalnych oporów przy
przepływ laminarny jest określany przez
formuła:
 MPa
MPa
gdzie

= a

Wielkie ilości
strata ciśnienia w standardzie
urządzenia hydrauliczne do
nominalne natężenie przepływu zwykle
wymienione w ich specyfikacjach technicznych.
1.5.2
Strata na
tarcie długości
to strata energii, która ma miejsce
w rurach prostych o stałym przekroju,
tych. z równomiernym przepływem płynu,
i rosną proporcjonalnie do długości
Rury. Straty te są spowodowane wewnętrznymi
tarcia w cieczy, a zatem mają
umieścić zarówno w szorstkich, jak i gładkich rurach.
Straty
ciśnienie tarcia w rurociągu
określa wzór Darcy:
 MPa
MPa
gdzie

ja
i d
- długość i średnica wewnętrzna rurociągu,
mm.
Ten
formuła ma zastosowanie zarówno do laminarnego,
jak również w przepływie turbulentnym; różnica
składa się tylko z wartości współczynnika

Na
przepływ laminarny (Re
Na
turbulentny współczynnik tarcia przepływu
jest nie tylko funkcją Re, ale
zależy również od chropowatości wewnętrznej
powierzchnia rury. Do hydraulicznie
gładki Rury,
tych. z chropowatością, która
praktycznie nie wpływa na jego odporność,
turbulentny współczynnik tarcia
tryb można określić za pomocą wzoru PC.
Konakowa:

rura
jest uważany za hydraulicznie płynny, jeśli
(d/k)>(Re/20),
gdzie k jest równoważną chropowatością,
mm. Na przykład w przypadku nowej stali bezszwowej
rury k≈0,03
mm, a po kilku latach eksploatacji
k≈0,2
mm, dla nowych rur bez szwu wykonanych z
metale nieżelazne k≈0,005
mm. Rury te są często używane w
układy hydrauliczne obrabiarek.
Współczynnik
tarcie w turbulentnym reżimie może być
określić według wzoru Altszulya,
bycie uniwersalnym (tj. mającym zastosowanie)
w każdym przypadku):

2. Charakterystyka przepływu modułu przepływu rurociągu
Zapamiętajmy
wzór na stratę liniową - wzór Darcy
- Weisbach:
 .
.
Wyrazić
w tym wzorze prędkość V
przez przepływ Q
ze stosunku
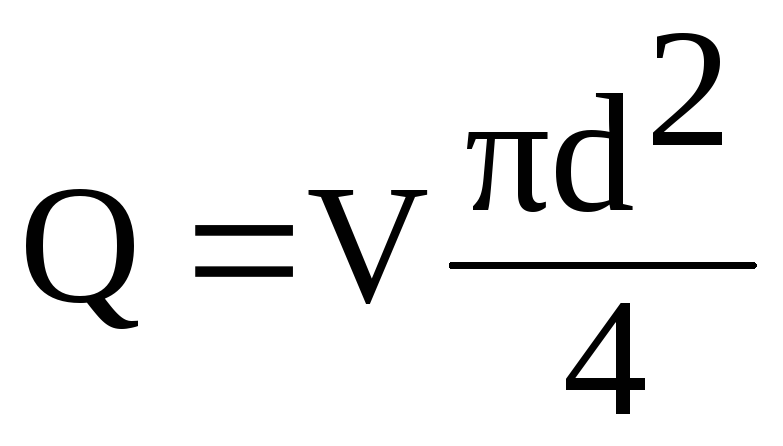
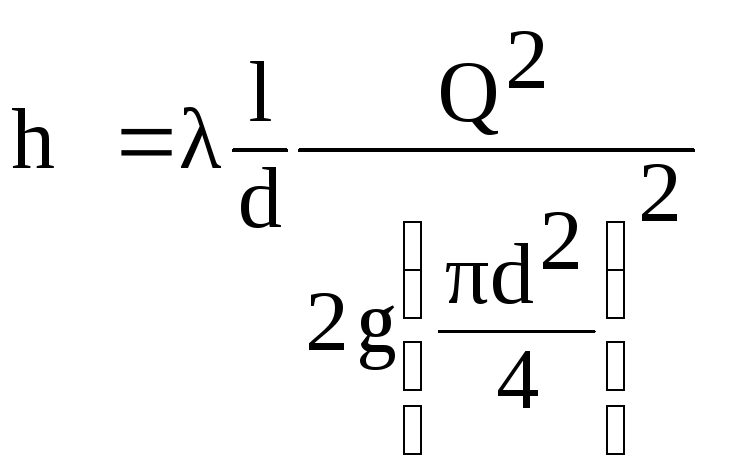
(6.1)
Do
rurociąg o określonej średnicy
kompleks wielkości
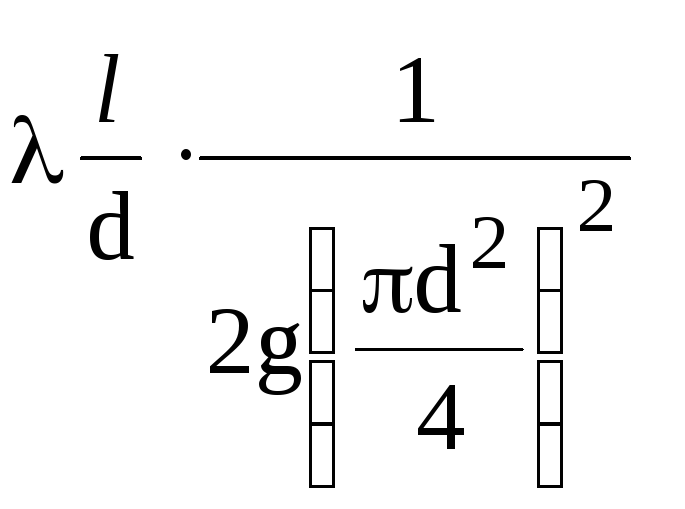
stała (1/K2),
z wyjątkiem współczynnika hydraulicznego
tarcie λ. Na podstawie koncepcji
średnia prędkość ekonomiczna Vs.e
pokażmy, że wskazany współczynnik λ
można przypisać temu kompleksowi, ponieważ v
W takim przypadku liczba Reynoldsa będzie
mają określone znaczenie:
 ,
,
a na wykresie Nikuradze współczynnik λ in
ten przypadek będzie miał specyficzny
oznaczający.
Uzasadniać
zasadność wprowadzenia koncepcji
średnia prędkość ekonomiczna w następujący sposób
rozumowanie.
hydrauliczny
system, np. hydraulika,
możesz pominąć pewien wydatek
wykonane z rur o różnych średnicach. Na
Jednocześnie wraz ze wzrostem średnicy d,
dlatego spadek prędkości V
nakłady inwestycyjne wzrosną oraz
koszty operacyjne będą
spadek z powodu spadku hydrauliki
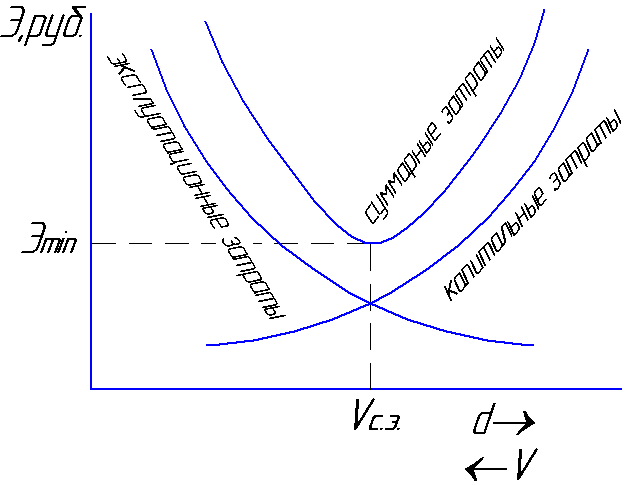
straty. Szybkość, z jaką suma
koszty będą minimalne
zostanie nazwany przeciętnym ekonomicznym
prędkość Vs.e
= 0,8 ... 1,3 m / s (ryc. 6.1).
rys.6.1
Następnie
wzór na stratę liniową (6.1) przyjmuje postać
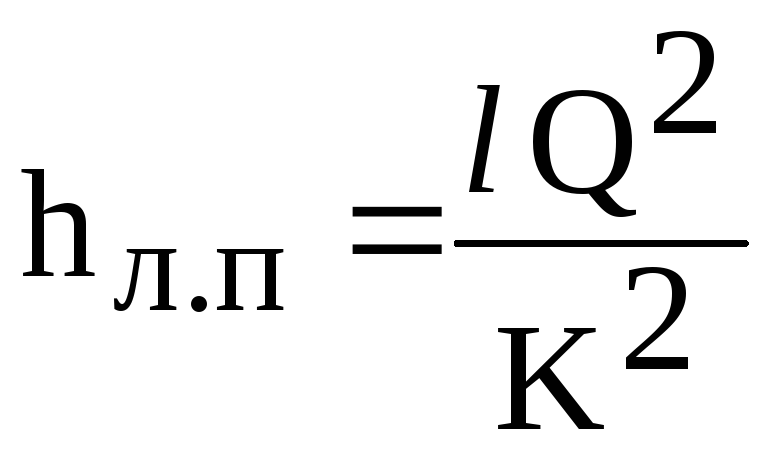
(6.2)
gdzie
K - charakterystyka przepływu rurociągu
(moduł płynięcia), zależny od materiału
rurociąg, średnica i przepływ. jest zajęty
ze stołów.
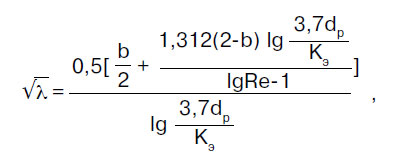
 ),C
),C ,
,